Hexo

Posted on Edited on

Preface

学校计算几何专题刚刚好讲完，放一下计算几何用到的板子；

Content

Problem

前摇：常见常数，误差比较

由于计算几何常常带有浮点类型的运算经常等号判定会有偏差，所以这里采用误差比较的方式判定相等；

1
2
3
4
5
6
7
8
9
10
11
12
13
typedef double db;
constexpr double eps=1e-6;
const double pi=acos(-1);
int sign(double k){   
    if (k>eps) return 1; 
    else if (k<-eps) return -1; 
    return 0;
}
int dbcmp(double x,double y){
    if(y-x>eps) return 1;
    else if(y-x<-eps) return -1;
    return 0;
}

常见的二维几何对象

点模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
template<typename T>struct point { // 点类
	T x, y;
	bool operator == (const point &a) const {
		return (abs(x - a.x) <= eps && abs(y - a.y) <= eps);
	}
	bool operator < (const point &a) const {
		if (abs(x - a.x) <= eps) return y < a.y;
		return x < a.x;
	}
	T length2() const {
		return (*this) * (*this);
	}
	T length() const {
		return sqrt(length2());
	}
	point unit() {
		double len = length();
		return {x / len, y / len};
	}
	point operator -() const {
		return { -x, -y};
	}
	point operator + (const point &a) const {
		return {x + a.x, y + a.y};
	}
	point operator - (const point &a) const {
		return {x - a.x, y - a.y};
	}
	point operator * (const T k) const {
		return {k * x, k * y};
	}
	point operator / (const T k) const {
		return {x / k, y / k};
	}
	T operator * (const point &a) const {
		return x * a.x + y * a.y;
	}
	T operator ^ (const point &a) const {
		return x * a.y - y * a.x;
	}
	point rotate(const double rad) const {
		double c = cos(rad), s = sin(rad);
		return {x*c - y * s, x*s + y * c};
	}
	point rotate90() const {
		return { -y, x};
	}
	double get_angle (const point &a) const {
		return atan2(y, x);
	}
	friend istream & operator >> (istream&, point &a) {
		scanf("%lf %lf", &a.x, &a.y);
		return cin;
	}
	friend ostream & operator << (ostream&, point &a) {
		printf(" ( %.6lf , %.6lf ) ", a.x, a.y);
		return cout;
	}
	// to-left测试
	int toleft (const point &a) const {
		const auto t = (*this)^a;
		return (t > eps) - (t < -eps);
	}
};

直线模板

1
2
3
4
5
6
7
8
9
template<typename T> struct line { 
	point<T>  p, v;
	bool operator == (const line &a) const {
		return abs(v ^ a.v) <= eps && abs(v ^ (p - a.p)) <= eps;
	}
	int toleft(const point<T> &a) const {
		return v.toleft(a - p);
	}
};

线段模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
template<typename T> struct segment {
	point<T> a, b;
	// -1 点在线段端点 | 0 点不在线段上 | 1 点严格在线段上
	int is_on(const point<T> &p) const {
		if (p == a || p == b) return -1;
		return (p - a).toleft(p - b) == 0 && (p - a) * (p - b) < -eps;
	}
    
	// -1 直线经过线段端点 | 0 线段和直线不相交 | 1 线段和直线严格相交
	int is_inter(const line<T> &l) const {
		if (l.toleft(a) == 0 || l.toleft(b) == 0) return -1;
		return l.toleft(a) != l.toleft(b);
	}
    
	// -1 在某一线段端点处相交 | 0 两线段不相交 | 1 两线段严格相交
	int is_inter(const segment<T> &s) const {
		if (is_on(s.a) || is_on(s.b) || s.is_on(a) || s.is_on(b)) 				return -1;
		const line<T> l {a, b - a}, ls {s.a, s.b - s.a};
		return l.toleft(s.a) * l.toleft(s.b) == -1 && 
            	ls.toleft(a) * ls.toleft(b) == -1;
	}

	// 点到线段距离
	long double dis(const point<T> &p) const {
		if ((p - a) * (b - a) < -eps || (p - b) * (a - b) < -eps) 				return min(p.dis(a), p.dis(b));
		const line<T> l {a, b - a};
		return l.dis(p);
	}

	// 两线段间距离
	long double dis(const segment<T> &s) const {
		if (is_inter(s)) return 0;
		return min({dis(s.a), dis(s.b), s.dis(a), s.dis(b)});
	}
};

普通多边形模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
template<typename T> struct polygon {
	std::vector<point<T>> p;//逆时针存储
	inline size_t nxt(const size_t i) const {
		return i == p.size() - 1 ? 0 : i + 1;
	}
	inline size_t pre(const size_t i) const {
		return i == 0 ? p.size() - 1 : i - 1;
	}
	pair<bool, int> winding(const point<T> &a) const {
		int cnt = 0;
		for (size_t i = 0; i < p.size(); i++) {
			point<T> u = p[i], v = p[nxt(i)];
			if (abs((a - u) ^ (a - v)) <= eps && (a - u) * (a - v) <= eps) return {true, 0}; 
             // 点a在线段uv上
			if (abs(u.y - v.y) <= eps) continue;
			line<T> uv = {u, v - u};
			if (u.y < v.y - eps && uv.toleft(a) <= 0) continue; // 方向向上且不在左侧
			if (u.y > v.y + eps && uv.toleft(a) >= 0) continue; // 方向向上且不在右侧
			if (u.y < a.y - eps && v.y >= a.y - eps) cnt++; // 向上穿过
			if (u.y >= a.y - eps && v.y < a.y - eps) cnt--; // 向下穿过
		}
		return {false, cnt};
	}

	// 计算周长
	double perimeter() const {
		double sum = 0;
		for (size_t i = 0; i < p.size(); i++) sum += dist(p[i], p[nxt(i)]);
		return sum;
	}
	// 计算面积
	double area() const {
		double sum = 0;
		for (size_t i = 0; i < p.size(); i++) sum += p[i] ^ p[nxt(i)];
		return abs(sum) / 2;
	}
};

圆模板

1
2
3
4
5
6
7
8
9
template<typename T> struct circle { 
	point<T>  o;
	T r;
	int is_in(const point<T> &q) const {
		point<T> qo=q-o;
		return (qo.length()-r)<=-eps;
	}
};

点与点之间（向量与向量）之间的关系

极角排序

利用库函数极角排序

先将所有点的极角算出来，然后按极角的值进行排序,不是将 atan2(y,x) 函数写在排序的比较函数里；

注意，atan2(double y,double x) 函数返回的是原点至点 $$( x , y )$$的方位角，即与与x轴正半轴的夹角，范围是$$(-\pi,\pi \ ]$$；

在极角排序中如果返回的极角值相同则按与原点距离升序；

相对于外积排序这个速度更快，但是可能有精度问题，如果一直$$WA$$就考虑把这个换掉；

注意：使用atan2（）应该先传y再传x；

1
2
3
4
5
6
7
8
9
10
11
bool cmp(point a, point b) {
    if(dcmp(atan2(a.y, a.x) - atan2(b.y, b.x)) == 0) 
        return a.x < b.x;
    return atan2(a.y, a.x) < atan2(b.y, b.x);
}//极点为原点时直接套用即可
point<double> o;
bool cmp(point a, point b) {
    if(dcmp(atan2(a.y-o.y, a.x-o.x) - atan2(b.y-o.y, b.x-o.x)) == 0) 
        return a.x < b.x;
    return atan2(a.y-o.y, a.x-o.x) < atan2(b.y-o.y, b.x-o.x);
} //改变api可以自定义极点

排序结果如图所示: $$A-B-C-D-E-F-G-H-I$$ ；

利用外积极角排序

一般利用外积可能会出现转一圈小于自己的情况，因为右手定则只能判断某两个的相对情况，所以我们利用象限作为排序的第一关键字就可以解决这个问题了；

相对于前者精度更优但是速度一般，如果题目有容错就不要写这个了；

1

点集的凸包

可以过一下这一道题；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
void Convex(vector<point<db>>&Convex_A,vector<point<db>>A){
	sort(A.begin(),A.end(),[](point<db>&l,point<db>&r){
		return l.x==r.x?l.y<r.y:l.x<r.x;
	});
	for(int i=1;i<A.size();i++) A[i]=A[i]-A[0];
	sort(A.begin()+1,A.end(),[](const point<db>&l,const point<db>&r){
		return sign(l^r)==0?l.length()<r.length():sign(l^r)>0;
	});
	for(int i=1;i<A.size();i++) A[i]=A[i]+A[0];
	Convex_A.resize(A.size());
	Convex_A[0]=A[0];
	Convex_A[1]=A[1];
	int cnt=2;
	for(int i=2;i<A.size();i++){
		while(cnt>1&&(sign((Convex_A[cnt-1]-Convex_A[cnt-2])^(A[i]-Convex_A[cnt-1]))<=0)) cnt--;
		Convex_A[cnt++]=A[i];
	}
	Convex_A.resize(cnt);
	return ;
}

int inquadrant(const point<db> &v){
	if(v.x>=0&&v.y>0) return 1;
	else if(v.x<0&&v.y>=0) return 2;
	else if(v.x<=0&&v.y<0) return 3;
	else if(v.x>0&&v.y<=0) return 4;
	else return 0;
}

const int maxn=1e5+5;
point<double> p[maxn];
point<double> cvx[maxn];
int tot,n;
bool cmp(point<db> l,point<db> r){
    return (sign(l^r)==0)
	?(l.length()<r.length())
	:sign(l^r)>0;
}
signed main ()
{
	int n;
	cin>>n;
	for(int i=0;i<n;i++) cin>>p[i];
	sort(p,p+n);
	for(int i=1;i<n;i++) p[i]=p[i]-p[0];
	sort(p+1,p+n,cmp);
	for(int i=1;i<n;i++) p[i]=p[i]+p[0];
	cvx[0]=p[0];
	cvx[1]=p[1];
	tot=2;
	for(int i=2;i<n;i++){
		while(tot>1&&(sign((cvx[tot-1]-cvx[tot-2])^(p[i]-cvx[tot-1]))<=0)) tot--;
		cvx[tot++]=p[i];
	}
	cvx[tot]=cvx[0];
    db ccc=0;
    for(int i=0;i<tot;i++){
        ccc+=(cvx[i+1]-cvx[i]).length();
    }
    //printf("%.2lf",ccc);
	int m;
	cin>>m;
	while(m--){
		point<db> v;
		cin>>v;
		if(tot==1) {
			if(v.x!=cvx[0].x||v.y!=cvx[0].y) cout<<"NO"<<endl;
			else cout<<"YES"<<endl;
		}
		else if(tot==2){
			segment<db> l={cvx[0],cvx[1]};
			if(l.is_on(v)==0) cout<<"NO"<<endl;
			else cout<<"YES"<<endl;
		}
		else{
			point<db> oa=cvx[1]-cvx[0];
			point<db> ov=v-cvx[0];
			point<db> ob=cvx[tot-1]-cvx[0];
			if(sign(oa^ov)<0) cout<<"NO"<<endl;
			else if(sign(oa^ov)==0){
				segment<db> l={cvx[0],cvx[1]};
				if(l.is_on(v)==0) cout<<"NO"<<endl;
				else cout<<"YES"<<endl;
			}
			else if(sign(ob^ov)>0) cout<<"NO"<<endl;
			else if(sign(ob^ov)==0){
				segment<db> l={cvx[0],cvx[tot-1]};
				if(l.is_on(v)==0) cout<<"NO"<<endl;
				else cout<<"YES"<<endl;
			}
			else{
				int l=1,r=tot-1,mid=0;
				while(l<r){
					mid=(l+r)/2;
					point om=cvx[mid]-cvx[0];
					if(sign(om^ov)==0) l=r=mid;
					else if(sign(om^ov)<0) r=mid;
					else l=mid+1;
				}
				point lr=cvx[l]-cvx[l-1];
				point lv=cvx[l]-v;
				if(sign(lr^lv)<=0) cout<<"YES"<<endl;
				else cout<<"NO"<<endl;
			}
		}
	}
	return 0;
}

点定位（$$PIP$$问题）

点定位问题大致分为三种方法：外积二分法，光线投影法，$$Winding \ Number$$（回转数法）；

其中，外积二分基于凸多边形的三角剖分，常与点集的凸包联系起来，通过确定极点并二分极角序确定点的位置；光线投影法属于扫描线算法的一种；回转数法适用于任意多边形，但是其经典形式存在着一定的精度问题；

平面最近点对

判断点与直线（射线，线段）的位置关系

$$ToLeftTest$$ : 判断点是否在直线的左侧

在上面的点模板和直线模板中也有用到，所以也可以引用上面的结构体内联的函数；

$$ToLeftTest$$ 就是利用向量的外积判断正负，外积为正说明在右手转过的角小于 $$\pi$$ ,点在直线左侧，大于$$\pi$$ 则说明点在直线右侧，如果等于零，在直线两点和该点构成的三角形面积为零，因此在直线上；

1
2
3
int to_left(const line<double> &l, const point<double> &p) {
	return l.v.toleft(p - l.p);
}

点到直线距离

在直线上取两点可以转化为三角形的高，利用外积求出面积，利用距离公式求出底；

1
2
3
double dist(const line<double> &l, const point<double> &p) {
	return abs(l.v ^ (p - l.p)) / l.v.length();
}

点到直线的投影点

利用内积关于投影的性质，将向量运算转化为模运算；

1
2
3
point<double> projection(const line<double> &l, const point<double> &p) {
	return l.p + l.v * ((l.v * (p - l.p)) / (l.v * l.v));
}

两直线交点

1
2
3
point<double> intersection(const line<double> &a, const line<double> &b) {
	return a.p + a.v * ((b.v ^ (a.p - b.p)) / (a.v ^ b.v));
}

判断直线与直线（射线、线段）的关系

半平面以及半平面交

判断圆与点、线、圆的关系

两圆的位置关系：相等，相离，内含，外切，内切，相交；

倒不如说考虑问题应该按照这个顺序想，因为前面的特殊情况往往蕴含着不一样的答案；

1
2
3
4
5
6
7
8
9
10
11
12
//两圆关系：5相离，4外切，3相交，2内切，1内含 
int relationcircle(circle k1,circle k2){
    db d=k1.o.dis(k2.o);
    db l=fabs(k1.r-k2.r);
    if(sign(d)==0&&sign(l)==0) return 0;
    else if(sign(d-k1.r-k2.r)>0)return 5;
    else if(sign(d-k1.r-k2.r)==0)return 4;
    else if(sign(d-k1.r-k2.r)<0 && sign(d-l)>0)return 3;
    else if(sign(d-l)==0)return 2;
    else if(sign(d-l)<0)return 1; 
    else exit(0);// to check another error
}

圆与圆的面积交问题

很明显在最朴素相交情况下，两圆面积交可以表示为两个弓形的面积之和，这样我们就转化为容斥原理求解即可；

注意我们这里使用$$Heron$$公式求解三角形的面积，尽量绕开对反三角的求解；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
int relationcircle(circle k1,circle k2){
    db d=k1.o.dis(k2.o);
    db l=fabs(k1.r-k2.r);
    if(sign(d)==0&&sign(l)==0) return 0;
    else if(sign(d-k1.r-k2.r)>0)return 5;
    else if(sign(d-k1.r-k2.r)==0)return 4;
    else if(sign(d-k1.r-k2.r)<0 && sign(d-l)>0)return 3;
    else if(sign(d-l)==0)return 2;
    else if(sign(d-l)<0)return 1; 
    else exit(0);
}
db circlearea(circle k1,circle k2){
    int rel=relationcircle(k1,k2);
    if(rel>=4)return 0.0;
    if(rel<=2)return min(k1.area(),k2.area());
    db d=k1.o.dis(k2.o);
    db hf=(k1.r+k2.r+d)/2.0;
    db ss=2*sqrt(hf*(hf-k1.r)*(hf-k2.r)*(hf-d));//Heron
    db a1=acos((k1.r*k1.r+d*d-k2.r*k2.r)/(2.0*k1.r*d));
    a1=a1*k1.r*k1.r;
    db a2=acos((k2.r*k2.r+d*d-k1.r*k1.r)/(2.0*k2.r*d));
    a2=a2*k2.r*k2.r;
    return a1+a2-ss;
}

圆与多边形面积交问题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
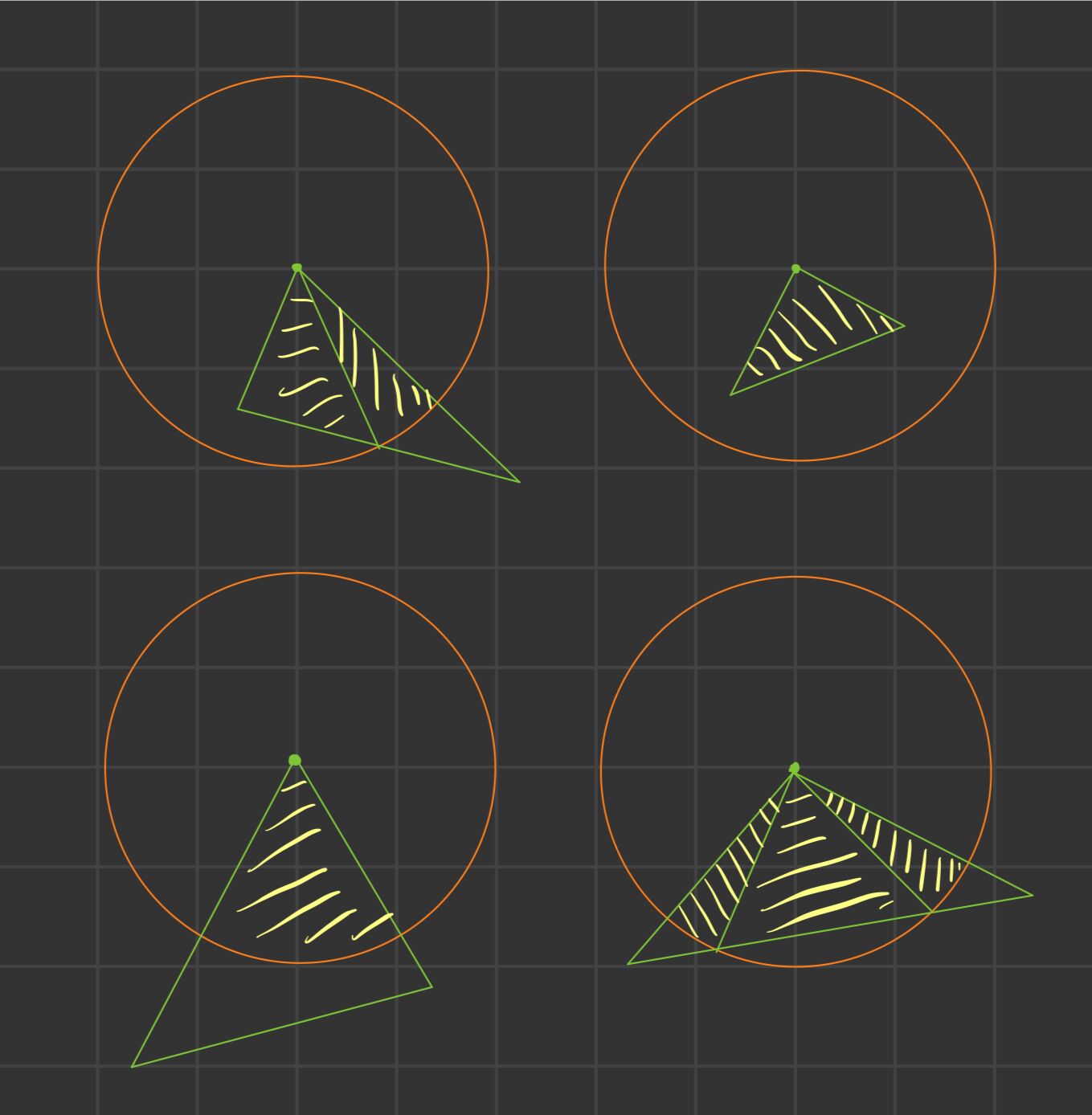
246
//#pragma GCC optimize(2)
#include<bits/stdc++.h>
#include<iostream>
using namespace std;
typedef double db;
constexpr double eps=1e-5;
const double pi=acos(-1);
int sign(double k){   
    if (k>eps) return 1; 
    else if (k<-eps) return -1; 
    return 0;
}
int dbcmp(double x,double y){
    if(y-x>eps) return 1;
    else if(y-x<-eps) return -1;
    return 0;
}
template<typename T>struct point { // 点类
	T x, y;
	bool operator == (const point &a) const {
		return (abs(x - a.x) <= eps && abs(y - a.y) <= eps);
	}
	bool operator < (const point &a) const {
		if (abs(x - a.x) <= eps) return y < a.y;
		return x < a.x;
	}
	T length2() const {
		return (*this) * (*this);
	}
	T length() const {
		return sqrt(length2());
	}
	point unit() {
		double len = length();
		return {x / len, y / len};
	}
	point operator -() const {
		return { -x, -y};
	}
	point operator + (const point &a) const {
		return {x + a.x, y + a.y};
	}
	point operator - (const point &a) const {
		return {x - a.x, y - a.y};
	}
	point operator * (const T k) const {
		return {k * x, k * y};
	}
	point operator / (const T k) const {
		return {x / k, y / k};
	}
	T operator * (const point &a) const {
		return x * a.x + y * a.y;
	}
	T operator ^ (const point &a) const {
		return x * a.y - y * a.x;
	}
	point rotate(const double rad) const {
		double c = cos(rad), s = sin(rad);
		return {x*c - y * s, x*s + y * c};
	}
	point rotate90() const {
		return { -y, x};
	}
	double get_angle (const point &a) const {
		return atan2(y, x);
	}
	friend istream & operator >> (istream&, point &a) {
		scanf("%lf %lf", &a.x, &a.y);
		return cin;
	}
	friend ostream & operator << (ostream&, point &a) {
		printf(" ( %.6lf , %.6lf ) ", a.x, a.y);
		return cout;
	}
	// to-left测试
	int toleft (const point &a) const {
		const auto t = (*this)^a;
		return (t > eps) - (t < -eps);
	}
};


template<typename T> struct line { 
	point<T>  p, v;
	bool operator == (const line &a) const {
		return abs(v ^ a.v) <= eps && abs(v ^ (p - a.p)) <= eps;
	}
	int toleft(const point<T> &a) const {
		return v.toleft(a - p);
	}
	int is_on(const point<T> &q) const {
		point<T> pq=p-q;
		return abs((pq^v))<=eps;
	}
};
template<typename T> struct segment {
	point<T> a, b;
	// -1 点在线段端点 | 0 点不在线段上 | 1 点严格在线段上
	int is_on(const point<T> &p) const {
		if (p == a || p == b) return -1;
		return (p - a).toleft(p - b) == 0 && (p - a) * (p - b) < -eps;
	}
    
	// -1 直线经过线段端点 | 0 线段和直线不相交 | 1 线段和直线严格相交
	int is_inter(const line<T> &l) const {
		if (l.toleft(a) == 0 || l.toleft(b) == 0) return -1;
		return l.toleft(a) != l.toleft(b);
	}
    
	// -1 在某一线段端点处相交 | 0 两线段不相交 | 1 两线段严格相交
	int is_inter(const segment<T> &s) const {
		if (is_on(s.a) || is_on(s.b) || s.is_on(a) || s.is_on(b)) 				
		return -1;
		const line<T> l {a, b - a}, ls {s.a, s.b - s.a};
		return l.toleft(s.a) * l.toleft(s.b) == -1 && 
            	ls.toleft(a) * ls.toleft(b) == -1;
	}

	// 点到线段距离
	double dis(const point<T> &p) const {
		if ((p - a) * (b - a) < -eps || (p - b) * (a - b) < -eps) 				
		return min(p.dis(a), p.dis(b));
		const line<T> l {a, b - a};
		return l.dis(p);
	}

	// 两线段间距离
	double dis(const segment<T> &s) const {
		if (is_inter(s)) return 0;
		return min({dis(s.a), dis(s.b), s.dis(a), s.dis(b)});
	}
};
template<typename T> struct circle { 
	point<T>  o;
	T r;
	int is_in(const point<T> &q) const {
		point<T> qo=q-o;
		return (qo.length()-r)<-eps;
	}
};

int getSegCircleIntersection(line<db> L,circle<db> C,
vector<point<db>>& sol) {
	double a=L.v.x;
	double b=L.p.x-C.o.x;
	double c=L.v.y;
	double d=L.p.y-C.o.y;
	double e=a*a+c*c;
	double f=2*(a*b + c*d);
	double g=b*b+d*d-C.r*C.r;
	double delta=f*f-4*e*g;
	double t1,t2;
	int ans = 0;
	if(sign(delta)<0) return 0;
	if(sign(delta)==0) {
		t1=t2=-f/(2*e);
		if(sign(t1)>=0&&sign(t1-1)<=0){
			ans++;
			sol.push_back(L.p+L.v*t1);
		}
		return ans;
	}
	t1=(-f-sqrt(delta))/(2*e);
	t2=(-f+sqrt(delta))/(2*e);
	if(t1>t2) swap(t1,t2);
	if(sign(t1)>=0&&sign(t1-1)<=0){
		ans++;
		sol.push_back(L.p+L.v*t1);
	}
	if(sign(t2)>=0&&sign(t2-1)<= 0) {
		ans++;
		sol.push_back(L.p+L.v*t2);
	}
	return ans;
}
double TriangleArea(point<db>A,point<db> B,point<db> C) {
	return (double)(fabs((B-A)^(C-A)) )/ 2;
}
double Angle(point<db> A, point<db> B) {
	if(sign(A^B)==0) return 0;
	return (double)acos(A*B / A.length() / B.length());
}
double IntersectionArea(circle<db> C,point<db> A,point<db> B) {
	if((A==B)|| (B ==C.o)||(C.o==A)) return 0;
	line<db> L={A,B-A};
	int cnt=0;
	bool inA, inB;
	if(inA=C.is_in(A)) cnt++;
	if(inB=C.is_in(B)) cnt++;
	if(cnt == 2) return TriangleArea(C.o, A, B);
	if(cnt == 1) {
		vector<point<db>> q;
		getSegCircleIntersection(L, C, q);
		if(inB) swap(A, B);
		double theta = Angle(q[0]-C.o, B-C.o);
		return C.r*C.r*theta/2 + TriangleArea(C.o, A, q[0]);
	}

	vector<point<db>> q;
	int sz = getSegCircleIntersection(L, C, q);
	if(sz <= 1) {
		double theta = Angle(A-C.o, B-C.o);
		return C.r*C.r*theta/2;
	}

	double theta = Angle(C.o-A, C.o-q[0]) + Angle(C.o-B,C.o-q[1]);
	return C.r*C.r*theta/2 + TriangleArea(C.o,q[0], q[1]);
}
void solve(){
    int n;
    db k;
    cin>>n>>k;
    vector<point<db>> poly(n);
	for(int i=0;i<n;i++) cin>>poly[i];
	point<db> T,S;
	cin>>T>>S;
	// point<db> X=S*(1/(k+1))+T*(k/(k+1));
	// point<db> Y=S*(1/(1-k))+T*(k/(k-1));
	point<db> M=S*(1/(1-k*k))-T*((k*k)/(1-k*k));
	db rr=(S-T).length()*k/(1-k*k);
	circle<db> C={M,rr};

	double ans=0;
	for(int i=0;i<n;i++){
		int sgn;
		if( sign(((poly[i]-C.o)^(poly[(i+1)%n]-C.o)))>0) sgn = 1;
		else sgn=-1;
		ans+=sgn*IntersectionArea(C, poly[i], poly[(i+1)%n]);
	}
	printf("%e\n",fabs(ans));
	return ;
}
int main ()
{
    //ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
    #ifdef local
    freopen("in.txt","r",stdin);
    freopen("out1.txt","w",stdout);
    #endif // local

    int t;
    cin>>t;
    while(t--) solve();
    return 0;
}

圆的面积并问题

可以打这个板子

圆外一点对圆的切线问题

两圆的公切线问题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
int get_tangents(circle A, circle B, pnode *a, pnode *b){
    int cnt = 0;        //存切点用
    if(dcmp(A.r - B.r) < 0)
    {
        swap(A, B);
        swap(a, b);
    }
    double d = sqrt((A.x - B.x) * (A.x - B.x) + (A.y - B.y) * (A.y - B.y));     //圆心距
    double rdiff = A.r - B.r;      //两圆半径差
    double rsum  = A.r + B.r;       //两圆半径和
    if(dcmp(d - rdiff) < 0)
        return 0;        //1.内含
    double base = atan2(B.y - A.y, B.x - A.x);      //向量AB的极角
    if(dcmp(d) == 0) return -1;        //2.重合
    if(dcmp(d - rdiff) == 0)
    {       //3.内切
        a[cnt] = b[cnt] = A.point(base);
        cnt++;
        return 1;
    }
    double ang = acos((A.r - B.r) / d);
    a[cnt] = A.point(base + ang); b[cnt] = B.point(base + ang); cnt++;      //4.相交（外切、外离的外公切线也在此求出）
    a[cnt] = A.point(base - ang); b[cnt] = B.point(base - ang); cnt++;      //两条外公切线的切点
    if(dcmp(d - rsum) == 0)
    {        //5.外切
        a[cnt] = b[cnt] = A.point(base);
        cnt++;
    }
    else if(dcmp(d - rsum) > 0)
    {      //6.外离
        double ang = acos((A.r + B.r) / d);
        a[cnt] = A.point(base + ang); b[cnt] = B.point(PI + base + ang); cnt++；
        a[cnt] = A.point(base - ang); b[cnt] = B.point(PI + base - ang); cnt++;
    }
    return cnt;
}

圆与直线的反演变换

最小圆覆盖

$$Ἀπολλώνιος$$圆

凸集问题

动态凸包

Minkowski Sum

来测下板子啊

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
void Minkowski(vector<point<db>>&s,vector<point<db>> a,vector<point<db>> b){
    int n=a.size();
    int m=b.size();
    vector<point<db>> s1,s2;
    for(int i=0;i<n;i++) s1.push_back(a[(i+1)%n]-a[i]);
    for(int i=0;i<m;i++) s2.push_back(b[(i+1)%m]-b[i]);
    int i=0,j=0,cnt=0;
    s.push_back(a[0]+b[0]);
    while(i<n&&j<m){
        if(sign(s1[i]^s2[j])>=0) s.push_back(s[cnt++]+s1[i++]);
        else s.push_back(s[cnt++]+s2[j++]);
    }
    while(i<n) s.push_back(s[cnt++]+s1[i++]);
    while(j<m) s.push_back(s[cnt++]+s2[j++]);
}

基本几何量的计算

三角形的有向面积（逆时针为正）

我们知道，两个向量的外积表示某个平行四边形的面积，那么我们只需要计算三角形两条边的向量外积的一半就是这个三角形的有向面积，实际面积即为有向距离的绝对值；

1
2
3
4
5
6
double triarea(Point p, Point q, Point s){
     return 
       0.5*(p.x * q.y - p.y * q.x
       + q.x * s.y - q.y * s.x
       + s.x * p.y - s.y * p.x);
 }

三角形$$Heron$$公式（三个顶点不知情况下）

Pick定理与整点问题

计算几何与数据结构

KD-Tree

Example

Remark

1

Posted on Edited on

Preface

整理题解的时候正好路过的知识黑洞，填补一手；

Content

Problem

如何将大范围的数据找到它们的排名数组，也即离散化；

使用线段树、树状数组解决“单点修改区间查询“，“区间修改单点查询”，”区间修改区间查询“，”区间最值“等问题

给定长度为$$n$$的排列，找到这个排列的逆序对个数；

Solution

离散化

对每个数和其下标捆绑排序 ，方便找到原来的位置；

1
2
3
4
5
6
7
8
9
10
11
12
13
14
vector<long long>a;
vector<int> discretization(vector<long long>&a){
    int n=a.size();
    vector<int> res(n);
    vector<pair<long long,int>> tmp;
    for(int i=0;i<n;i++)tmp.push_back({a[i],i});
    sort(tmp.begin(),tmp.end(),[](pair<long long,int>&l,pair<long long,int>&r){
        return l.first==r.first?l.second<r.second:l.first<r.first;
    });
    int rk=1;
    for(int i=0;i<n;i++) res[tmp[i].second]=(i==0||tmp[i].first==tmp[i-1].first)?rk:++rk;
    return res;
}
vector<int> rnk=discretization(a);

$$Segment\ Tree$$

综述

  • 线段树是一种二叉平衡树，支持维护区间和，区间最值，区间异或和等多种信息，要求对维护的运算存在结合律和存在幺元；
  • 线段树也支持对单点修改，区间修改，区间查询，同时也支持对线段树之间的合并，删除点等操作，能够处理比线段数组更加复杂的问题；

含义

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
template<typename T,auto op,auto e,typename F,
auto mp,auto cp,auto e1>class segtree{
//op,e,mp,cp都是函数指针，op是满足结合律的运算，e是群中的幺元,
//mp是利用lazy修改树上的值的函数，cp是lazy的下放运算，e1是lazytag置零
    int n;
    vector<T> tr;
    vector<F> lazy;
    void pushup(int k) {tr[k]=op(v[k<<1],v[(k<<1)+1]);}
    void pushdown(int pos,int l,int r){
        tr[pos]=mp(tr[pos],lazy[pos],l,r);
        if(l!=r) {
            lazy[pos<<1]=cp(lazy[pos<<1],lazy[pos]);
            lazy[1+(pos<<1)]=cp(lazy[1+(pos<<1)],lazy[pos]);
        }
        lazy[pos]=e1();
    }
    void modify(int now,int ql,int qr,int l,int r,F x){
        //pushdown(now,l,r);
        if(l>qr||r<ql) return;
        if(l<=ql&&r>=qr) {
            lazy[now]=x;
            pushdown(now,l,r);
            return;
        }
        modify(now<<1,ql,qr,l,l+((r-l)>>1));
        modify(1+(now<<1),ql,qr,1+l+((r-l)>>1),r);
        pushup(now);
    }
    void set(int now,int pos,int l,int r,T x){
        if(l>pos||r<pos) return ;
        if(l==r&&r==pos) {tr[now]=x;return ;}
        set(now<<1,pos,l,l+((r-l)>>1),x);
        set(1+(now<<1),pos,1+l+((r-l)>>1),r,x);
        pushup(now);
    }
    T query(int now,int ql,int qr,int l,int r){
        if(l>ql||r<qr) return e();
        if(l>=ql&&r<=qr) return tr[now];
        return op(query(now<<1,ql,qr,l,l+((r-l)>>1)),query(1+(now<<1),ql,qr,1+l+((r-l)>>1)),r);
    }
public:
    segment(int _n){n=_n;v=vector<T>(n<<2,e())}
    void set(int pos,T x){set(1,l,1,n,x);return ;}
    T query(int l,int r){return query(1,l,r,1,n);}
};

$$Finwick\ Tree$$

综述

  • 对于输入一个长度为$$n$$的数组$$a$$,其数状数组也是一个长度为$$n$$的数组$$Bitr$$，数组中的每个元素维护着一个区间的区间和;

  • 数状数组解决的问题下标需要从1开始,确保计算$lowbit$能到正确的位置；

  • 树状数组解决的是一类动态前缀和问题，能够在$$O(logn)$$实现数组的单点修改与区间查询，而朴素算法只能在$$O(1)$$内解决修改（查询）而在$$O(n)$$内解决查询（修改）；

  • 区间最大公约数，区间最值可移步线段树；

含义

  • $$Bitr [i]$$和其维护区间$$[l_i,r_i]$$的关系

    • 树状数组的下标就是区间的右端点，换言之,$$r_i=i$$;
    • $$Bitr[i]$$维护的区间长度等于$$i$$的二进制表示中最右端的$$1$$所代表的$$2$$的幂次，换言之，$$r_i-l_i+1=lowbit(i)=i&(-i)$$
    • 树状数组的第$$i$$位维护的区间为$$[i-(i&(-i))+1,i]$$,可以理解为每次线段树中二分的两个区间左边的那一个；
    • $$Bitr [i]$$维护区间$$[i-(i&(-i))+1,i]$$的和，换言之，$$Bitr [i]=\sum_{t=i-lowbit(i)+1}^{i}a[t]$$

  • $$Bitr$$如何求解区间和$$\sum_{l\le t\le r}a[t]$$

    • $$\sum_{l\le t\le r}a[t]=\sum_{i=1}^{r}a[i]-\sum_{i=1}^{l-1}a[i]$$转化为前缀和之差来求解
    • 将$$[1,x]$$递归地拆分成若干个区间$$[1,x]=[1,x-lowbit(x)]\cup[x-lowbit(x)+1,x],x\gets x-lowbit(x)\ when\ x\ge1$$;

  • 更新$$a[t]$$如何修改$$Bitr$$

    • 我们需要知道$$t$$包含在哪些区间之内
    • 初始要更新的区间为$$[t-lowbit(t)+1,t]$$
      • 假设当前最新已经更新的区间为$$[l,r]$$,下一步要更新的区间为$$[u,v]$$,在线段树中二分区间左边的为$$[l,r]$$，那右边的那个区间（实际在树状数组中并不存在）左端点为$$r+1$$.长度为$$lowbit(r)$$,那么要更新的区间就是左右两个区间的并集，$$v-(r+1)+1=lowbir(r),v=r+lowbit(r)$$;
    • 我们递归地更新$$t\gets t+lowbit(t) \ when \ t\le n$$

  • 实现区间修改和原数组的单点查询

    • 引入差分数组：$$a[i]=\sum_{j=1}^{i}d[j],d[i]=\left{\begin{matrix}
      a[i] & i=1\
      a[i]-a[i-1] &i>1
      \end{matrix}\right.$$
    • 区间$$[l,r]$$内增加$$val$$，在差分数组中表现只有第$$l,r+1$$项发生变化，分别$$+val,-val$$;
    • 单点查询$$pos$$相当于求差分数组的前缀和，由于我们一直维护的都是差分数组所以原数组未更新；
    • 区间查询同样可以转化为前缀和之差，而前缀和$$\sum_{i=1}^{t}a[i]=(t+1)\sum_{i=1}^{t}d[i]-\sum_{i=1}^{t}id[i]$$,维护两个树状数组即可；

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
//注意这是C17的语言特性
template<typename T>struct BIT{
    #ifndef lowbit
    #define lowbit(x) ((x)&(-(x)))
    #endif
    static const int maxn=5e5+10;
    T n;
    T tr[maxn];
    T Diff_tr[maxn];
    T c[maxn];
    BIT<T> () {}
    void update(T pos,T val){//原数组的单点更新
        while(pos<=n){
            tr[pos]+=val;
            pos+=lowbit(pos);
        }
        return ;
    }
    T getPreSum(T r){//原数组的前缀和
        T res=0;
        while(r){
            res+=tr[r];
            r-=lowbit(r);
        }
        return res;
    }
    T getRangeSum(T l,T r){//原数组的区间和
        return getPreSum(r)-getPreSum(l-1);
    }
    void Diff_update(T pos,T val){//差分数组的单点更新
        while(pos<=n){
            Diff_tr[pos]+=val;
            c[pos]+=pos*val;
            pos+=lowbit(pos);
        }
        return ;
    }
    void Diff_RangeUpdate(T l,T r,T val){//差分数组的区间更新
        Diff_update(l,val);
        Diff_update(r+1,-val);
        return ;
    }
    T Single_query(T pos){//原数组的单点查询
        T res=0;
        while(pos){
            res+=Diff_tr[pos];
            pos-=lowbit(pos);
        }
        return res;
    }
    T PreSum_query(T r){
        T res=0;
        while(r){
            res+=(r+1)*Diff_tr[r]-c[r];
            r-=lowbit(r);
        }
        return res;
    }
    T Range_query(T l,T r){
        return PreSum_query(r)-PreSum_query(l-1);
    }
    void init(T(&a)[maxn],T _n){//原数组初始化为FinwickTree
        n=_n;
        memset(tr,0,sizeof(tr));
        memset(c,0,sizeof(c));
        memset(Diff_tr,0,sizeof(Diff_tr));
        for(int i=1;i<=n;i++){
            update(i,a[i]);
            Diff_update(i,i==1?a[i]:a[i]-a[i-1]);
        }
        return ;
    }
};

逆序对

逆序对当然很容易用树状数组来求出，先将数据离散化，统计

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
#define local
//#pragma GCC optimize(2)
#include<bits/stdc++.h>
#include<iostream>
using namespace std;
const int maxn=5e5+10;
template<typename T>struct BIT{
    #ifndef lowbit
    #define lowbit(x) ((x)&(-(x)))
    #endif
    static const int maxn=5e5+10;
    T n;
    T tr[maxn];
    T Diff_tr[maxn];
    T c[maxn];
    BIT<T> () {}
    void update(T pos,T val){//原数组的单点更新
        while(pos<=n){
            tr[pos]+=val;
            pos+=lowbit(pos);
        }
        return ;
    }
    T getPreSum(T r){//原数组的前缀和
        T res=0;
        while(r){
            res+=tr[r];
            r-=lowbit(r);
        }
        return res;
    }
    T getRangeSum(T l,T r){//原数组的区间和
        return getPreSum(r)-getPreSum(l-1);
    }
    void Diff_update(T pos,T val){//差分数组的单点更新
        while(pos<=n){
            Diff_tr[pos]+=val;
            c[pos]+=pos*val;
            pos+=lowbit(pos);
        }
        return ;
    }
    void Diff_RangeUpdate(T l,T r,T val){//差分数组的区间更新
        Diff_update(l,val);
        Diff_update(r+1,-val);
        return ;
    }
    T Single_query(T pos){//原数组的单点查询
        T res=0;
        while(pos){
            res+=Diff_tr[pos];
            pos-=lowbit(pos);
        }
        return res;
    }
    T PreSum_query(T r){
        T res=0;
        while(r){
            res+=(r+1)*Diff_tr[r]-c[r];
            r-=lowbit(r);
        }
        return res;
    }
    T Range_query(T l,T r){
        return PreSum_query(r)-PreSum_query(l-1);
    }
    void init(T(&a)[maxn],T _n){//原数组初始化为FinwickTree
        n=_n;
        memset(tr,0,sizeof(tr));
        memset(c,0,sizeof(c));
        memset(Diff_tr,0,sizeof(Diff_tr));
        for(int i=1;i<=n;i++){
            update(i,a[i]);
            Diff_update(i,i==1?a[i]:a[i]-a[i-1]);
        }
        return ;
    }
};
vector<int> discretization(vector<int>&a){
    int n=a.size();
    vector<int> res(n);
    vector<pair<long long,int>> tmp;
    for(int i=0;i<n;i++)tmp.push_back({a[i],i});
    sort(tmp.begin(),tmp.end(),[](pair<long long,int>&l,pair<long long,int>&r){
        return l.first==r.first?l.second<r.second:l.first<r.first;
    });
    int rk=1;
    for(int i=0;i<n;i++) res[tmp[i].second]=(i==0||tmp[i].first==tmp[i-1].first)?rk:++rk;
    return res;
}
vector<int> rnk;
vector<int> a;
int A[maxn];
BIT<int> b;
int main ()
{
    //ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
    #ifdef local
    freopen("in.txt","r",stdin);
    freopen("out.txt","w",stdout);
    #endif // local

    int n;
    cin>>n;
    for(int i=0;i<n;i++){
        int x;
        cin>>x;
        a.push_back(x);
    }
    rnk=discretization(a);
    b.init(A,n);
    for(int i=1;i<=n;i++) A[i]=rnk[i-1];
    long long cnt=0;
    for(int i=1;i<=n;i++){
        b.update(A[i],1);
        cnt+=(i-b.getPreSum(A[i]))*1ll;
    }
    cout<<cnt<<endl;
    return 0;
}

Example

Remark

Posted on Edited on

Preface

暑假集训用到了最短路的板子但之前的板子没存下来，在加上之前也看的不是很明白，故这里放点笔记；

部分板子目前还未测试过，谨慎使用$$(2023.7.15)$$；

Content

Problem

用链式前向星方式存储一个有权图$$G(V:E)$$，找到点 $$ i,j $$ 之间权值最小的路径长度；

注意：有时题目中的图其实就是树，而树的路径长度用 $$dfs$$ 就好了不需要用这个；

通常包括$$\ Dijstra 算法,SPFA \ and \ Floyd算法$$，其中小心SPFA被卡爆（）；

Solution

$$Dijstra$$ 算法

Notice:

  • 该算法只能处理边正权图的单源最短路问题，但是它的效率十分优秀，一般采用带小根堆优先队列优化（$$ZKW$$线段树!$$Fibonnaci$$堆!）；

  • 时间复杂度为$$O((|V|+|E|)log|V|)$$;

  • 但这个复杂度放在稠密图里可能会被$%$$$hack$$,需要换成邻接矩阵的方式存图，复杂度为$$O(|V|^2)$$,遇到了再补吧；

Proof：

  • 对于每个点$$v$$均维护一个「当前最短距离数组」$$dis[v]$$ 以及「访问数组」$$vis[v] $$,首先将$$dis[u]$$初始化为0，将其他点的距离初始化为无穷，并将所有点初始化为未访问的。记$$e[i]:u-v$$的边权为 $$e[i].w$$。然后进行以下步骤：
    1. 从所有未访问的点中，找出当前距离最小的,并将其标记为已访问的;
    2. 调整所有出边连接但尚未访问的点，转移状态；
    3. 重复1和2步骤，直到所有点都已访问，因为所有边权权值均为正的，所以用之后访问的结点是不能更新已经访问过的结点的（因为贪婪算法下若可以更新的话必定在还在之前就已经更新过了）；
    4. 可以用pre[y]=i维护最短的路径（点边关系）；

Template：

标准版询问单源最短路径

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
#define local
//#pragma GCC optimize(2)
#include<bits/stdc++.h>
#include<iostream>
using namespace std;

const int N=200005;
struct Edge{
    int head;
    int to;
    int nxt;
    int w;
}e[N];
void add(int u,int v,int w,int& cnt,std::vector<int>& head){
    e[cnt].nxt=head[u];
    head[u]=cnt;
    e[cnt].head=u,e[cnt].to=v,e[cnt].w=w;
    cnt++;
    return ;
}//链式前向星建图
//*****************************************************************************************//

long long dis[maxn]; 
//int pre[maxn];
const int INF=1000000009;
class Node{//使用Node维护每次要更新的点和距离
public:
    long long distance;
    int position;
    Node(long long a,int b){distance=a;position=b;}
    bool operator >(const Node&obj) const{
        return distance>obj.distance;
    };
};
class cmp{//小根堆比较函数
public:
    bool operator()(Node&a,Node&b)const{
        return a>b;
    }
};
std::priority_queue<Node,std::vector<Node>,cmp> disQ;
void Dijstra(int u,int n,long long (&dis)[maxn],std::vector<int>& head/*,int (&pre)[maxn]*/){
    for(int i=1;i<=n;i++) dis[i]=INF;
    dis[u]=0;
    disQ.push(Node(0,u));//保存用来更新的队列
    bool vis[maxn];
    memset(vis,false,sizeof(vis));//初始化

    while(!disQ.empty()){
        int x=disQ.top().position;
        disQ.pop();
        if(vis[x]) continue; vis[x]=true;//不再对已访问过的位置进行访问
        for(int j=head[x];j!=-1;j=e[j].nxt){
            int y=e[j].to;//遍历当前位置的邻点，并更新它们
            if(dis[y]>dis[x]+e[j].w){
                dis[y]=dis[x]+e[j].w;
                if(!vis[y]) disQ.push(Node(dis[y],y))/*,pre[y]=i*/;
            }
        }
    }
    return ;
}
//****************************************************************************************//

int main ()
{
    //ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
    #ifdef local
    freopen("in.txt","r",stdin);
    freopen("out.txt","w",stdout);
    #endif // local

    int n,m,s;
    std::cin>>n>>m>>s;

    int cnt=0;
    std::vector<int> head;//head[u],头为u的当前最晚出现的边标号
    head.resize(n+1,-1);
    for(int i=0;i<m;i++){
        int u,v,w;
        std::cin>>u>>v>>w;
        add(u,v,w,cnt,head);
    }
    //memset(pre,0,sizeof(pre));
    Dijstra(s,n,dis,head);
    for(int i=1;i<=n;i++){
        if(i!=1) printf(" ");
        std::cout<<dis[i];
    }
    return 0;
}

$$Floyd$$ 算法

Notice

  • $$Floyd$$ 算法是基于最朴素的动态规划的思想，求出全局上的任意两点的最短路问题，可以处理负边权的情况；
  • 我们知道对于图$$G$$ 中存在负权值环的话，沿着这个环一直前进是不会得到最短路的，$$Floyd$$ 算法也无法处理这类的问题；
  • 在一些加了若干限制的最短路问题中，往往都要回归到朴素的$$Floyd$$算法来；

Proof

考虑对每个$$k$$值，「$$i$$到$$j$$ 的路径只允许经过标号不大于$$k$$的点」中最短路径长度$$dis[i][j]$$，明显$$k=n$$是我们所求问题的答案；

  • 初始$$k=0$$，所欲值都是正无穷；

  • 递归的说，对于已有的$$k-1 $$允许的最短路径，新的最短路径要么经过$$k$$,要么维持不变；

  • 状态转移方程为
    $$
    dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]),for\ all\ (i,j)s
    $$

  • 时间复杂度为$$O(|V|^3)$$;

Template:

弱化版单源最短路径，不是正解，只有70分

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
//#pragma GCC optimize(2)
#include<bits/stdc++.h>
#include<iostream>
const int maxn=10005;
const int N=500005;

long long dis[maxn][maxn]; 
const long long INF= (1<<31)-1;
void Floyd(int n,long long (&dis)[maxn][maxn]){
    for(int k=1;k<=n;k++){
        for(int i=1;i<=n;i++){
            for(int j=1;j<=n;j++){
                dis[i][j]=std::min(dis[i][j],dis[i][k]+dis[k][j]);
            }
        }
    }
    return ;
}
int main ()
{
    //ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
    #ifdef local
    freopen("in.txt","r",stdin);
    freopen("out.txt","w",stdout);
    #endif // local

    int n,m,s;
    std::cin>>n>>m>>s;

    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            dis[i][j]= INF;
        }
    }
    for(int i=0;i<m;i++){
        int u,v,w;
        std::cin>>u>>v>>w;
        dis[u][v]=std::min(dis[u][v],w*1LL);//可能由重边
    }
    
    Floyd(n,dis);
    for(int i=1;i<=n;i++){
        if(i!=1) printf(" ");
        std::cout<<((i!=s)?dis[s][i]:0);
    }
    return 0;
}

$$SPFA$$ 算法

Notice:

  • 对于一般的带权图，不同于正权图的$$relax$$操作每次取出最小的$$dis$$来进行下一步，边权有负数是不保证正确性的，所以我们维护一个普通的队列就行了，这也是$$SPFA$$经常得卡爆的地方，构造数据可以欺骗算法进入冗余的分支，使得队列的进出和$$relax$$多了很多不必要的操作；
  • 这个算法本质是$$Bellmon-Ford$$算法的局部优化，复杂度为$$O(|V||E|)$$；
  • 所以说没必要仔细解释$$Bellmon$$算法对全局的$$n-1$$次$$relax$$操作了，卡$$SPFA$$的一定卡$$Bellmon$$;
  • （保证输入是随机数据）慎用，不要偷懒！因为它已经死了；

Template:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
//#pragma GCC optimize(2)
#include<bits/stdc++.h>
#include<iostream>
const int maxn=100005;

const int N=500005;
struct Edge{
    int head;
    int to;
    int nxt;
    int w;
}e[N];
void add(int u,int v,int w,int& cnt,std::vector<int>& head){
    e[cnt].nxt=head[u];
    head[u]=cnt;
    e[cnt].head=u,e[cnt].to=v,e[cnt].w=w;
    cnt++;
    return ;
}
//******************************************************************************//
const long long INF=(1<<31)-1;
long long dis[maxn];
void SPFA(int s,int n,long long (&dis)[maxn],std::vector<int> &head){
    for(int i=1;i<=n;i++) dis[i]=INF;
    dis[s]=0;
    bool vis[maxn];
    memset(vis,false,sizeof(vis));

    std::queue<int> disQ;
    disQ.push(s);
    while(!disQ.empty()){
        int x=disQ.front();
        disQ.pop();
        vis[x]=false;
        for(int i=head[x];i!=-1;i=e[i].nxt){
            int y=e[i].to;
            if(dis[y]>dis[x]+e[i].w){
                dis[y]=dis[x]+e[i].w;
                if(!vis[y]){
                    vis[y]=true;
                    disQ.push(y);
                }
            }
        }
    }
}
//*************************************************************************************//
int main ()
{
    //ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
    #ifdef local
    freopen("in.txt","r",stdin);
    freopen("out.txt","w",stdout);
    #endif // local

    int n,m,s;
    std::cin>>n>>m>>s;

    int cnt=0;
    std::vector<int> head;//head[u],头为u的当前最晚出现的边标号
    head.resize(n+1,-1);
    for(int i=0;i<m;i++){
        int u,v,w;
        std::cin>>u>>v>>w;
        add(u,v,w,cnt,head);
    }
    //memset(pre,0,sizeof(pre));
    SPFA(s,n,dis,head);
    for(int i=1;i<=n;i++){
        if(i!=1) printf(" ");
        std::cout<<dis[i];
    }
    return 0;
}

Example

暂时没有；

洛谷P3385 【模板】负环

洛谷P5909【模板】Johnson 全源最短路

Remark

还是多整理一些模板少打比赛吧，太坐牢了，怎么写那么快的啊；

学校的专题等一波题解发下来吧，真的不知道里面是什么毒瘤数据；

Posted on Edited on

Preface

作为暑假集训的第一篇博客，为什么是#4呢？因为终于写出了免于爆零了 ，感慨良多，虽然在赛场上一直卡G（英语不好读不懂题），但明显感觉到卷子的难度正在适应我的水平，而且几何和字符串专题根本做不动，借着这个契机开始整理笔记（感觉学习曲线过于陡峭了）；

赛后补题只补了六道，留坑记录一下；

A:cf245D 1500 二进制
B:cf1557B 1100 排序
C:cf1338B 1800 构造
D:cf1430E 1900 转换后求逆序对
E:cf915F 2400（虚高） 并查集
F:cf1668C 1300 暴力，贪心
G:cf176D 2100 有些技巧的DP
H:cf448D 1800 二分答案

#A. Restoring Table

题源：CF245D

题意：

给定对称矩阵和规模n,满足如下关系，要求还原数组a
$$
b_{ij}=\left{\begin{matrix}-1
& i=j\a_{i} & a_{j}
& i \ne j
\end{matrix}\right.
$$

思路：

  • 对每个b做二进制拆分不难发现还原a只需要对相应下标做按位且运算即可，而且确实如题目所说答案并不唯一；
  • 本场签到题；

AC code：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
#include<bits/stdc++.h>
using namespace std;

int main ()
{
    #ifdef local
    freopen("in.txt","r",stdin);
    freopen("out.txt","w",stdout);
    #endif // local

    int n;
    const int maxn=105;
    int a[maxn];
    memset(a,0,sizeof(a));
    int b[maxn][maxn];
    cin>>n;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            cin>>b[i][j];
        }
    }
    for(int j=1;j<=n;j++){
        b[j][j]=0;
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            a[i]|=b[i][j];
        }
    }
    for(int i=1;i<=n;i++){
        if(i!=1) cout<<" ";
        cout<<a[i];
    }
    return 0;
}

#B. Moamen and k-subarrays

题源：CF1557B

题意：

询问能否将长度为n的数组分成k块，重新排列得到顺序；

思路：

  • 我们考察可以把原数组的若干个数绑定在一起的块，若能重新排列得到顺序，那么块里的数必然在顺序排列中也是相连的；
  • 如果原数组这样分块后存在（可能不到）k个块，那么把一些好的块打散肯定也是符合题意的；
  • 考虑原地排序还原下标，依次遍历检查相邻两数能否组块，采用pair输入；
  • 也是签到题，但是没看榜后面的时间all in G题了（所以这场没有到）；

AC code：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include<bits/stdc++.h>
#include<iostream>
using namespace std;
const int maxn=300005;
 
int main ()
{
    #ifdef local
    freopen("in.txt","r",stdin);
    freopen("out.txt","w",stdout);
    #endif // local
 
    int t;
    std::cin>>t;
    while(t--){
        int n,k;
        std::cin>>n>>k;
        std::vector<pair<int,int> > v(n);
        for(int i=0;i<n;i++){
            std::cin>>v[i].first;
            v[i].second=i;
        }
        std::vector<pair<int,int> > u=v;
        std::sort(v.begin(),v.end());
        int cnt=1;
        for(int i=1;i<n;i++){
            if(v[i-1].second+1!=v[i].second) cnt++;
        }
        if(cnt<=k) cout<<"YES"<<endl;
        else cout<<"NO"<<endl;
    }
    return 0;
}

#C. Edge Weight Assignment

题源：CF1338B

题意：

没读；

思路：

没有；

#D. String Reversal

题源：CF1430E

题意：

将字符串对换成其反串最少的操作次数；

思路：

  • 开始陷入误区尝试证明最少的次数是正串和反串逆序对差的绝对值，结果样例都跑不过，换思路；
  • 直接模拟对换过程，猜想不做故意浪费的操作换回来又换回去即为最小次数；
  • 建立一个目标数组，即每个字符最终应该到达的下标位置，考虑到有重复字符要做到某种意义的最优应使得对于正串某个字符第i个目标是反串相同字符的第i个；
  • 对目标数组最终变为自然排列，因而最少的次数就是这个字符串的逆序对个数，归并排序即可；
  • 这个转化初见，有些巧妙的，留坑归并排序、树状数组的模板整理于此（做这个题时也没学过归并排序，线段树写不下去了思路还是错的就摘了个板子过来还没仔细看看）；
  • 复杂度 O（n logn) ;

AC code：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#include<bits/stdc++.h>
#include<iostream>
using namespace std;
typedef long long ll;
const int maxn=200006;
ll ans=0;
void msort(int* tar,int* tmp,int l,int r){
    if(l==r) return ;
    int mid=l+((r-l)>>1);
    msort(tar,tmp,l,mid);
    msort(tar,tmp,mid+1,r);
    int i=l,j=mid+1,k=l;
    while(i<=mid&&j<=r){
        if(tar[i]<=tar[j]) tmp[k++]=tar[i++];
        else tmp[k++]=tar[j++],ans+=mid-i+1;
    }
    while(i<=mid) tmp[k++]=tar[i++];
    while(j<=r) tmp[k++]=tar[j++];
    for(int p=l;p<=r;p++){
        tar[p]=tmp[p];
    }
    return ;
}
int star[maxn],stemp[maxn],ttar[maxn],ttemp[maxn];
int main ()
{
    #ifdef local
    freopen("in.txt","r",stdin);
    freopen("out.txt","w",stdout);
    #endif // local

    int n;
    cin>>n;
    string s;
    cin>>s;
    //string t=string(s.rbegin(),s.rend());
    memset(star,0,sizeof(star));
    memset(stemp,0,sizeof(stemp));
    stack<int> buc[26];
    for(int i=0;i<n;i++){
        int x=s[i]-'a';
        buc[x].push(n-1-i);
    }
    for(int i=0;i<n;i++){
        int x=s[i]-'a';
        star[i]=buc[x].top();
        buc[x].pop();
    }
    msort(star,stemp,0,n-1);
    cout<<ans<<endl;
    return 0;
}

#E. Imbalance Value of a Tree

题源：CF915F

题意：

给定树T以及树上结点赋点权a[i]，定义I（i，j）为i与j之间的路径经过点最大值与最小值之差，计算
$$
\sum_{i=1}^{n} \sum_{j=i}^{n} I(i,j)
$$

思路：

  • 开始采用树上倍增找到lca的做法，但是MLE了，毕竟确实开了很大的数组，而且也感觉会跑不过；

  • 但还是见的少了，本题是DSU模板题；

  • 首先观察到在树上路径操作，并且经过的边显然只取决于它的端点，考虑将点权转化为边权（常见套路），在考虑最大值问题时为两端点最大值，反之亦然；

  • 转化表达式，维护各个最大值和最小值贡献的次数，考虑最大值这一边的问腿，
    $$
    \sum_{i=1}^{n} \sum_{j=i}^{n} I(i,j)=\sum_{i=1}^{n} \sum_{j=i}^{n} \max_{e\in i\longrightarrow j} w_1(e)-\sum_{i=1}^{n} \sum_{j=i}^{n} \min_{e\in i\longrightarrow j} w_2(e)
    =\sum_{e\in T} w_1(e)p_1(e)-\sum_{e\in T} w_2(e)p_2(e)
    $$

  • p1(e)可以看作由e的权值决定这样路径i~j的条数，很明显权值越小能够能决定的路径数越少；

  • 将权值原地排序，用DSU维护边全局信息，两边相连则加入DSU中，对树做路径压缩的DSU总会转化为星状图，所以每次更新将贡献次数传递给父亲并更新DSU的状态就好了，并且开始做的点权转化使得每条边至少可以控制自己两个端点之间的路径（就是自己），所以初始化为1；

  • 要加上输入优化，不知道为什么跑出来差别那么大看起来真的输入了很多很多数来卡人，复杂度应该是略大于O(n)，这是由于路径压缩的DSU复杂度是近似常数，所以数据膨胀的飞起；

AC code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
#include<bits/stdc++.h>
#include<iostream>
using namespace std;
typedef long long ll;
const int maxn=1000006;
ll a[maxn],f[maxn],p[maxn];
int n;
ll ans=0;
class Edge{
    public:
    ll x,y,w;
}e[maxn];
bool cmp1(Edge&a,Edge&b){
    return a.w<b.w;
}
bool cmp0(Edge&a,Edge&b){
    return a.w>b.w;
}
ll find(ll x){
    return (f[x]==x)?x:f[x]=find(f[x]);//路径压缩
}
void init(bool op){
    for(int i=1;i<=n;i++){
        f[i]=i;
        p[i]=1;
    }
    
    for(int i=1;i<=n-1;i++){
        e[i].w=(op)?max(a[e[i].x],a[e[i].y]):min(a[e[i].x],a[e[i].y]);
    }
    sort(e+1,e+n,op?cmp1:cmp0);
    return ;
}
int main ()
{
    #ifdef local
    freopen("in.txt","r",stdin);
    freopen("out.txt","w",stdout);
    #endif // local

    scanf("%lld",&n);
    for(int i=1;i<=n;i++){
        scanf("%lld",a+i);
    }
    for(int i=1;i<=n-1;i++){
        scanf("%lld%lld",&e[i].x,&e[i].y);
    }
    init(1);
    for(int i=1;i<=n-1;i++){
        ll ex=find(e[i].x);//通过并查集等效出去的两端
        ll ey=find(e[i].y);
        ans+=e[i].w*(p[ex]*p[ey]);
        f[ey]=ex;
        p[ex]+=p[ey];
    }
    init(0);
    for(int i=1;i<=n-1;i++){
        ll ex=find(e[i].x);
        ll ey=find(e[i].y);
        ans-=e[i].w*(p[ex]*p[ey]);
        f[ey]=ex;
        p[ex]+=p[ey];
    }
    cout<<ans<<endl;
    return 0;
}

p.s.

看的出来对并查集也不是很熟悉，留个坑整理一下；

#F. Make it Increasing

题源：CF1668C

题意：

给定数组a，零初始化b,找到a[i]b[i]严格递增的数组b，最小化
$$
\sum_{i=1}^{n}|b[i]|
$$

思路：

  • 想法是活用负数，暴力找到一点置为0，左边为负数右边为正数；
  • 于是brute force枚举置零的位置，只需要比较当前最优方案即可；
  • 最优方案是贪心的使得b[i]a[i]从0位置开始看变化的缓慢一点，至少保证能递增的最低限度；
  • 试图优化了但直接WA了一发，因为找不到确切的i，枚举变化陡峭的点也是在O(n)的，比如1 1 4 5 1 4 重复；
  • 复杂度$$ O(n^2) $$

AC code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#include<bits/stdc++.h>
#include<iostream>
using namespace std;
typedef long long ll;
const int maxn=5005;
int main ()
{
    #ifdef local
    freopen("in.txt","r",stdin);
    freopen("out.txt","w",stdout);
    #endif // local

    int n;
    cin>>n;
    vector<ll>a(n+1);
    vector<double>k(n+1);
    for(int i=1;i<=n;i++){
        cin>>a[i];
    }
    // int cnt=0;
    // double km=0;
    // for(int i=2;i<=n;i++){
    //     k[i]=(a[i]+0.0)/a[i-1];
    //     km=std::max(k[i],km);
    // }
    vector<ll> id;
    for(int i=1;i<=n;i++){
        //if(k[i]==km) 
        id.push_back(i); 
    }
    int num=id.size();
    ll best=0;
    for(int j=0;j<num;j++){
        int pos=id[j];
        ll sum=0;
        vector<ll> b(n+1);
        for(int i=pos+1;i<=n;i++){
            b[i]=ceil((1.0+b[i-1]*a[i-1])/a[i]);
            sum+=b[i];
        }
        for(int i=pos-1;i>=1;i--){
            b[i]=-ceil((1.0-b[i+1]*a[i+1])/a[i]);
            sum-=b[i];
        }
        best=(j==0)?sum:std::min(best,sum);
    }
    cout<<best<<endl;
    return 0;
}

#G. Hyper String

题源：CF176D

题意：

没看

思路：

没有

#H. Multiplication Table

题源：CF448D

题意：

找到m·n的乘法表中非去重非递减第k大的数；

思路：

  • 比赛的时候感觉html彻底崩了，读了好几遍题目没有读懂里面几个单词的意思，一直以为是要去重的所以连样例也没读懂但好多人都过了也不懂，反正当时就懵逼的一批这也是掉大分的罪魁祸首（）；
  • 感觉去重的话可能是个超级大容斥加筛法；
  • 赛后发题源秒懂这就是二分的签到题（）；
  • 对每次折半询问一个数，在表里算出不大于它的数的个数；
  • 复杂度O(nlogmn),让我们一起学习二分吧；

AC code：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include<bits/stdc++.h>
#include<iostream>
using namespace std;
typedef long long ll;
int main(){
    #ifdef local
    freopen("in.txt","r",stdin);
    freopen("out.txt","w",stdout);
    #endif

    ll n,m,k;
    cin>>n>>m>>k;
    if(n<m) swap(n,m);
    ll l=1,r=m*n;
    while(l<r){
        ll tmp=0;
        ll x=l+(r-l)/2;
        for(int i=1;i<=n;i++){
            tmp+=min(m,x/i);
        }
        if(tmp<k) l=x+1;
        else r=x;
    }
    cout<<l<<endl;
    return 0;
}

Remark

  • 大概率是过不了线了感觉学的东西已经应付不过来了，如果没有进入的话正好留点时间给自己整理一下；
  • 没爆零就是win；

Posted on Edited on

Preface

第五场，2023.7.14的比赛，好像这次歪榜比较严重，写完$$A$$就没时间看$$B$$了，但是$$B$$好像挺简单的；

#A.

题源：Gym - 103828A

题意：

给定两个数列$$A,G$$，要求构造字典序最小的数列$$P$$: 若$$i \ne j,A_i\ge A_j,G_i=G_j$$,则$$P_i>P_j$$,若不存在输出$$-1$$;

思路：

一眼由于自反性$$A_i\ge A_j$$的等号取不到，若存在$$A_i=A_j,G_i=G_j,i\ne j$$,则输出$$-1$$;

将$$A$$中的数按照$$G_i$$的值作为一个桶放进去，再桶内排出大小，由于要求$$P$$的字典序最小，所以要根据下标使得$$P_i$$取尽量小的值，我们设置一个时间戳数组，顺序遍历$$A$$，若当前$$A_i$$时间戳为$$0$$（未访问过）,那么进入$$A_i$$所在的桶，遍历桶中的尚未赋上时间戳的数，给他们赋上相应的时间戳，直到在桶中找到$$A_i$$的值停止，给桶打上相应标记方便下次进入直接从标记开始;

AC code：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
#define local
//#pragma GCC optimize(2)
#include<bits/stdc++.h>
#include<iostream>
using namespace std;
const int maxn=100005;
struct arr{
    int a;
    int g;
    int id;
}x[maxn];
vector<int> buc[maxn];
int f[maxn],ans[maxn],flag[maxn],fg[maxn];
bool vis[maxn];
int main ()
{
    //ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
    #ifdef local
    freopen("in.txt","r",stdin);
    freopen("out.txt","w",stdout);
    #endif // local

    int t;
    cin>>t;
    while(t--){
        int n;
        cin>>n;
        memset(x,0,sizeof(x));
        memset(f,0,sizeof(f));
        memset(ans,0,sizeof(ans));
        memset(vis,false,sizeof(vis));
        memset(flag,0,sizeof(flag));
        memset(fg,0,sizeof(fg));
        for(int i=1;i<=n;i++){
            cin>>x[i].a;
            x[i].id=i;
        }
        int mx=0;
        for(int i=1;i<=n;i++){
            cin>>x[i].g;
            mx=max(mx,x[i].g);
        }
        for(int i=0;i<=maxn;i++){
            buc[i].clear();
        }
        sort(x+1,x+n+1,[](arr&l,arr&r){
            return l.a<r.a;
        });
        for(int i=1;i<=n;i++){
            int lab=x[i].g;
            buc[lab].push_back(x[i].id);
            f[x[i].id]=lab;
            fg[x[i].id]=i;
        }
        bool error=false;
        for(int i=1;i<=mx;i++){
            int sz=buc[i].size();
            for(int j=0;j<sz-1;j++){
                if(x[fg[buc[i][j]]].a==x[fg[buc[i][j+1]]].a)
                {
                    error=true;
                    break;
                }
            }
            if(error) break;
        }
        if(error) {
            cout<<-1<<endl;
        }
        else{
            int time=0;int pos=1;
            for(pos=1;pos<=n;pos++){
                if(vis[pos]==false){
                    int k=f[pos];
                    int r=flag[k];
                    for(;buc[k][r]!=pos;r++){
                        if(vis[buc[k][r]]==true) continue;
                        ans[buc[k][r]]=++time;
                        vis[buc[k][r]]=true;
                    }
                    ans[buc[k][r]]=++time;
                    flag[k]=r+1;
                }
            }
            for(int i=1;i<=n;i++){
                if(i!=1) cout<<" ";
                cout<<ans[i];
            }
            cout<<endl;
        }
    }
    return 0;
}

#B.

题源：Gym - 103828D

题意：

对字符串做$$n$$次$$ctrl+A+C+V$$，找到字典序第$$k$$位；

思路：

在比赛的时候想找到二进制下的规律结果什么也没看出来；

后来的某一天在看时，发现直接用归纳的角度来看，标签是指$$-Ci$$,如果我们已经有了$$n-1$$情况的表，那么可以将$$n$$ 情况的表分成三个部分，比如说样例$$(X,2)$$所有可能的$$k$$值构成的表（假设$$X=Acm2022-23,Y=Acm2022-23-C0000$$）：

  • 第一部分只有一个串，即为原串$$X$$
  • 第二部分有$$2^{n-1}$$个串，可以看成$$(Y,n-1)$$ 的表直接粘贴，即$$Y,Y-C0000$$
  • 第三部分有$$2^{n-1}-1$$个串，可以看成在$$(X,n-1)$$的表中除去原串，复制过后，每个串的第一个标签递增$$1$$,即$$X-C0000$$递增$$1$$后，为$$X-C0001$$

注意一些细节，标签递增要把标签$$-Ci$$那个数$$i$$给取出来，以及直接比较$$k\le 1+2^{n-1}$$会爆long long;

AC code：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
//#pragma GCC optimize(2)
#include<bits/stdc++.h>
#include<iostream>
using namespace std;
const int maxn=1005;
typedef long long ll;
bool cp(ll k,ll n){
    ll u=0;
    ll uu=1;
    while(uu<k-1) {
        uu<<=1;
        u++;
    }
    return u<n;
}//比较k<=1+(1<<n-1)
string dp(string&x,ll n,ll k){
    if(k==1||n==0) return x;
    string t=x+"-C0000";
    if(k>=2&&cp(k,n)) return dp(t,n-1,k-1);
    else {
        string y=dp(x,n-1,k-(1LL<<n-1));
        int c1=y[x.size()+2]-'0';
        int c2=y[x.size()+3]-'0';
        int c3=y[x.size()+4]-'0';
        int c4=y[x.size()+5]-'0';
        int c=c1*1000+c2*100+c3*10+c4;
        c+=1;
        y[x.size()+5]=c%10+'0';c/=10;
        y[x.size()+4]=c%10+'0';c/=10;
        y[x.size()+3]=c%10+'0';c/=10;
        y[x.size()+2]=c%10+'0';c/=10;
        return y;
    }
    return "";
}
void solve(){
    string s;
    cin>>s;
    long long n,k;
    cin>>n>>k;
    cout<<dp(s,n,k)<<endl;
    return;
}
int main ()
{
    //ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
    #ifdef local
    freopen("in.txt","r",stdin);
    freopen("out.txt","w",stdout);
    #endif // local

    int t;
    cin>>t;
    while(t--)solve();
    return 0;
}

#C.

题源：Gym - 103828I

题意：

思路：

AC code：

1

#D. Even Adjacent Product

题源：Gym - 103828J

题意：

输出一个长度为$$n$$的置换，使得相邻两数乘积为偶数

思路：

输出$$1$$到$$n$$即可；

AC code：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
//#pragma GCC optimize(2)
#include<bits/stdc++.h>
#include<iostream>
using namespace std;

int main ()
{
    //ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
    #ifdef local
    freopen("in.txt","r",stdin);
    freopen("out.txt","w",stdout);
    #endif // local

    int t;
    cin>>t;
    while(t--){
        int n;
        cin>>n;
        for(int j=1;j<=n;j++){
            if(j!=1) cout<<" ";
            cout<<j;
        }
        cout<<endl;
    }
    return 0;
}

#E.

题源：Gym - 103828H

题意：

组合计数，输出正多边形中筝形的个数；

思路：

首先，如果边数为奇数，是不存在筝形的；

其次，对于偶数的情况，我们按照对角线进行分类，与这条对角线垂直的对角线的两个端点，和原对角线两个端点构成筝形；

排除重复的情况（指筝形变成正方形），此时两条对角线长度相等；

AC code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#define local
//#pragma GCC optimize(2)
#include<bits/stdc++.h>
#include<iostream>
using namespace std;
typedef long long ll;
int main ()
{
    //ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
    #ifdef local
    freopen("in.txt","r",stdin);
    freopen("out.txt","w",stdout);
    #endif // local

    int t;
    cin>>t;
    while(t--){
        ll n,ans;
        cin>>n;
        if(n&1) ans=0;
        else {
            ll x=(n>>1)-1;
            if(x&1) ans=((n*(x-1))>>1)+((x+1)>>1);
            else ans=(n*x)>>1;
        }
        cout<<ans<<endl;
    }
    return 0;
}

#F.

题源：Gym - 104345L

题意：

思路：

AC code:

1

#G.

题源：Gym - 103828L

题意：

思路：

AC code：

1

#H. Drazil and Tiles

题源：CF515D

题意：

对于$$m\times n$$的表格，有些格子挖去，能否用唯一的方案用多米诺骨牌覆盖；

思路：

$$Hall$$匹配；

AC code：

1

#I.

题源：Gym - 104114G

题意：

给定一系列在水平线上咬合的齿轮坐标和所有的齿轮半径，找到从左到右各个齿轮的半径；

思路：

并没有什么好的办法，暴力搜索一个齿轮可能的半径，用这个数据反解出其他齿轮的半径，再检验是否符合要求；

用到的剪枝思路：

为了使得搜索的次数尽可能少，找到相邻两个齿轮半径之和最小的两个齿轮，搜索一个齿轮可能的半径，它一定比半径之和要小；

在检验答案的过程中，如果得出的半径明显不符合要求（小于可能的半径最小值或者大于可能的半径最大值），直接不考虑了；

AC code：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
#define local
//#pragma GCC optimize(2)
#include<bits/stdc++.h>
#include<iostream>
using namespace std;
typedef long long ll;
const int maxn=5e5+10;
ll x[maxn];
ll r[maxn];
ll d[maxn];
ll ans[maxn];
ll cpy[maxn];
int main ()
{
    //ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
    #ifdef local
    freopen("in.txt","r",stdin);
    freopen("out.txt","w",stdout);
    #endif // local

    int n;
    cin>>n;
    for(int i=1;i<=n;i++)cin>>x[i];
    for(int i=1;i<=n;i++)cin>>r[i];
    sort(r+1,r+n+1);
    for(int i=1;i<n;i++) d[i]=x[i+1]-x[i];
    ll mi=3e9;
    int fg=0;
    for(int i=1;i<n;i++) {
        if(mi>d[i]) {
            mi=d[i];
            fg=i;
        }
    }
    for(int i=1;i<=n;i++) {
        if(r[i]>=mi) break;
        bool err=false;
        ans[fg]=r[i];
        cpy[fg]=r[i];
        for(int j=fg-1;j>=1;j--){
            ans[j]=d[j]-ans[j+1];
            cpy[j]=d[j]-cpy[j+1];
            if(ans[j]<r[1]||ans[j]>r[n]){
                err=true;
                break;
            }
        }
        if(err) continue;
        for(int j=fg+1;j<=n;j++){
            ans[j]=d[j-1]-ans[j-1];
            cpy[j]=d[j-1]-cpy[j-1];
            if(ans[j]<r[1]||ans[j]>r[n]){
                err=true;
                break;
            }
        }
        if(err) continue;
        sort(cpy+1,cpy+n+1);
        for(int i=1;i<=n;i++) {
            if(cpy[i]!=r[i]) {
                err=true;
                break;
            }
        }
        if(!err) break;
    }
    for(int i=1;i<=n;i++) cout<<ans[i]<<" ";
    return 0;
}

Remark

![](https://kytolly-1318202921.cos.ap-chengdu.myqcloud.com/202307310229931.png

0%