Hexo

Posted on Edited on

Posted on Edited on

Posted on Edited on

Posted on Edited on

Posted on Edited on

Posted on

Preface

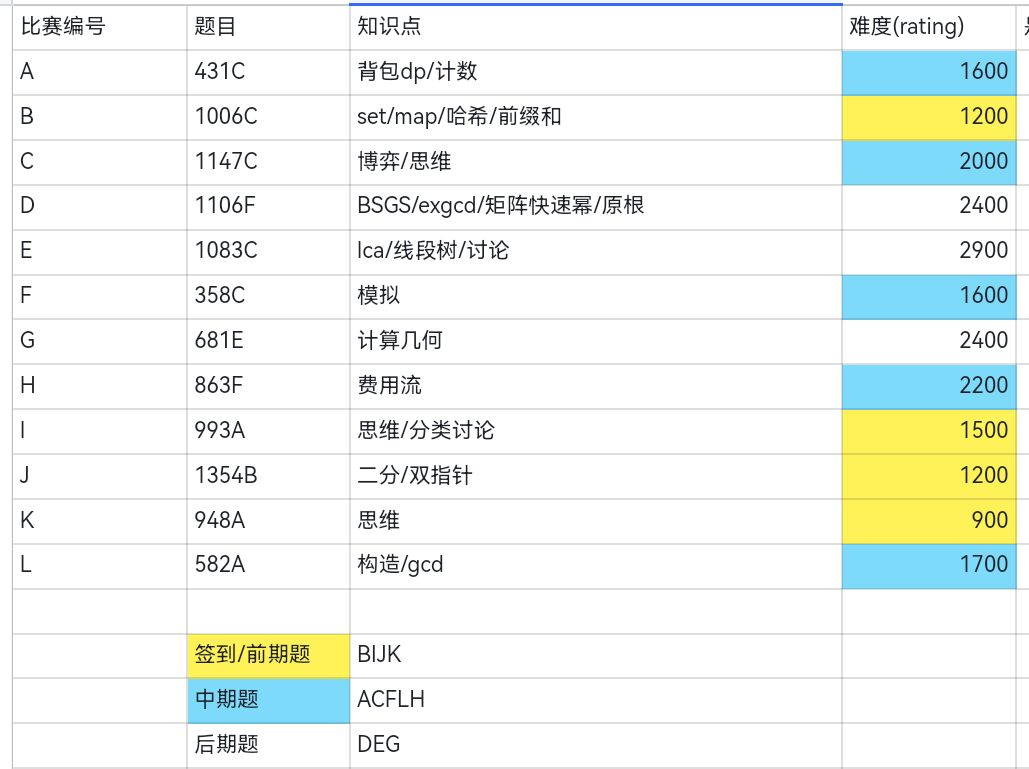
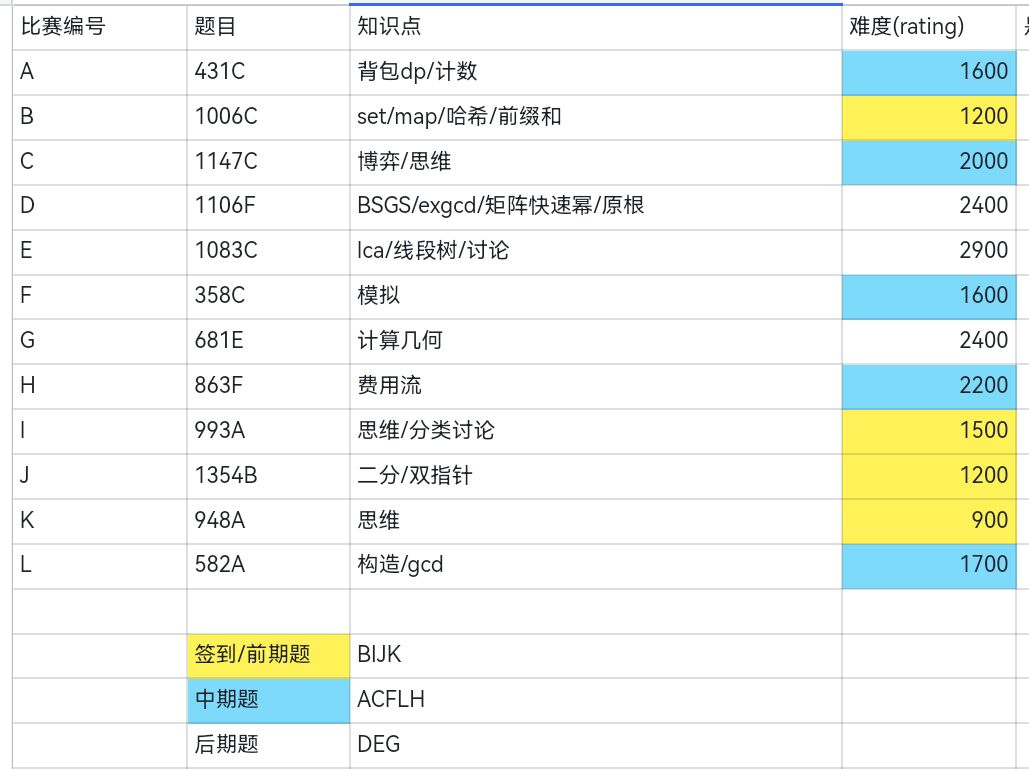
这是7.10的比赛，爆零告终；

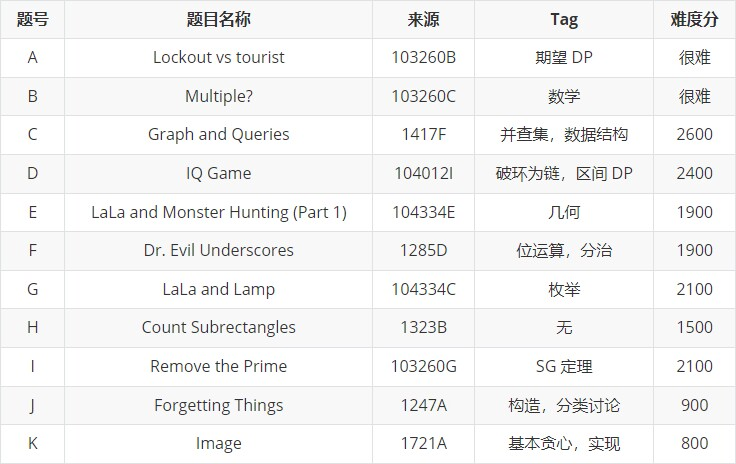
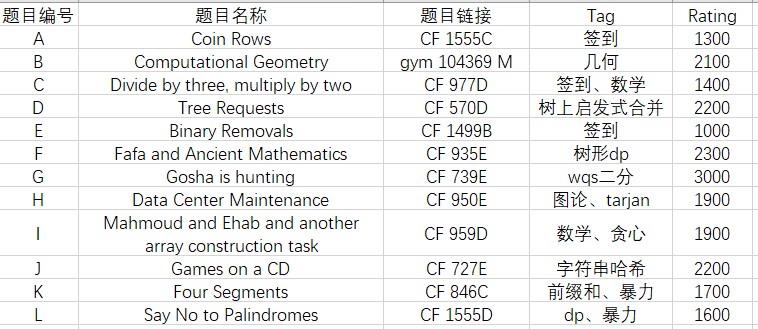
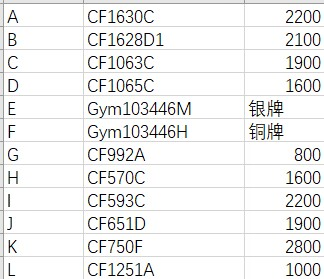
今天训练赛的GH题来自下面这场比赛的A题和C题：
https://codeforces.com/gym/103466
其余题来源于：
https://codeforces.com/gym/104197
第二个链接可以在下图位置找到其余题的题解;

Content

A. Adjacent Product Sum

题源： Gym - 104197A

题意：

给定$$n$$个正整数，希望重新排列而最大化相邻两项乘积循环和$$sum(a)=\sum_{i=1}^{n}a[i]a[i+1]$$

思路：

这样的循环和让人一眼想起女奥不等式，但是这里变量的取值都是固定的，所以不难想起使用局部调整法；

考察序列最大值$$M$$,和次大值$$A,B$$,若$$A,B$$不位于$$M$$的两侧，那么调整为$$M$$的两侧$$sum(a)$$不减(排序不等式)，设$$M$$两侧的数为$$a,b$$,$$A,B$$两侧的数为$$c,d,e,f$$：
$$
M(a+b)+A(c+d)+B(e+f)\le M(A+B)+a(c+d)+b(e+f)
$$
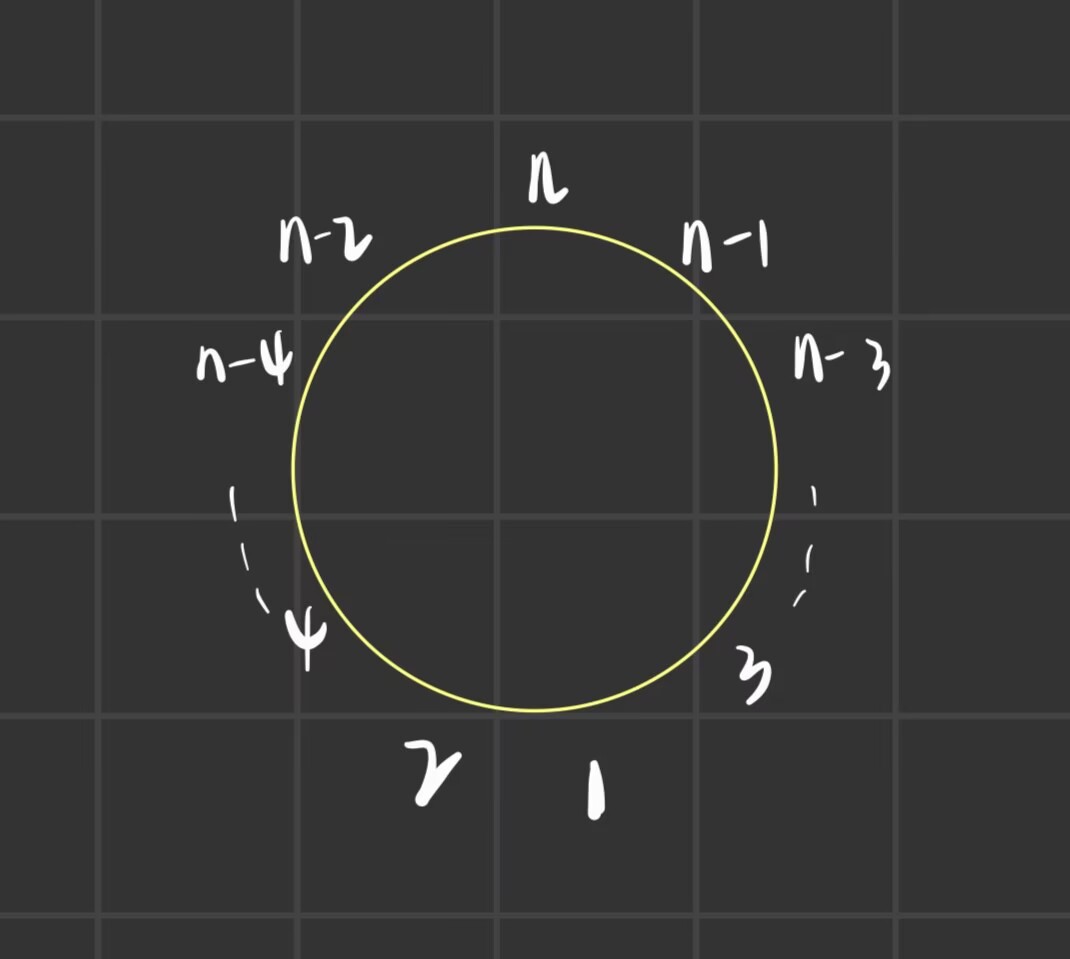
那么$$sum(a)=sum(a-{M})+M(A+B)-AB$$,变元个数递降，取等条件如图所示，用$$i$$来表示序列中第$$i$$小的数；

在调试的时候一直超时，当时也弄不明白什么原因，后来把数组开成int就过了，由于这道题的输入量很大，微小的效率问题都可能会超时，能开int一定不要开long long，不能开的一定要大胆开long long

AC code：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#define local
#include<bits/stdc++.h>
using namespace std;
const int maxn=200005;
typedef long long ll;

int main(){
    #ifdef local
    freopen("in.txt","r",stdin);
    freopen("out,txt","w",stdout);
    #endif

    int t; 
    scanf("%d",&t);
    while(t--){
        int n;
        scanf("%d",&n);
        int a[maxn];
        memset(a,0,sizeof(a));
        for(int i=0;i<n;i++){
            scanf("%d",&a[i]);
        }
        ll ans=0;
        sort(a,a+n);
        int order[n+1]={0};
        for(int i=1;i<n;i++){
            if(i&1) 
                order[(i>>1)+1]=i;
            else 
                order[n-(i>>1)]=i;
        }
        order[n]=0;
        for(int i=0;i<n;i++){
            ans+=1LL*a[(order[i])]*a[order[(i+1)%n]];
        }
        printf("%lld\n",ans);
    }
    return 0;
}

B. Distance Parities

题源：Gym - 104197D

题意：

给定连通图两两顶点最小距离的奇偶性，判断是否存在这样满足条件的图；

思路：

由于根本没有见过这种可能多解的问题卡了很久，事实上我们只需要给出自己的构造就好了；

我们注意到临界矩阵天然满足这样的奇偶性关系，我们假定输入的就是邻接矩阵，利用$$Floyd$$算法检查奇偶性是否成立，如果可以就还原原图，如果不行答案就是否定的；

AC code：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
#define local
#include<bits/stdc++.h>
#include<iostream>
using namespace std;
const int maxn=505;
int a[maxn][maxn];
long long dis[maxn][maxn]; 
const long long INF= (1<<30)-1;
void Floyd(int n,long long (&dis)[maxn][maxn]){
    for(int k=1;k<=n;k++){
        for(int i=1;i<=n;i++){
            for(int j=1;j<=n;j++){
                dis[i][j]=std::min(dis[i][j],dis[i][k]+dis[k][j]);
            }
        }
    }
    return ;
}
int main ()
{
    #ifdef local
    freopen("in.txt","r",stdin);
    freopen("out.txt","w",stdout);
    #endif // local

    int t;
    cin>>t;
    while(t--){
        int n;
        cin>>n;
        memset(a,0,sizeof(a));
        for(int i=1;i<=n;i++){
            for(int j=1;j<=n;j++){
                scanf("%1d",&a[i][j]);
            }
        }
        long long dis[maxn][maxn]; 
        for(int i=1;i<=n;i++){
            for(int j=1;j<=n;j++){
                if(a[i][j]) dis[i][j]=1;
                else dis[i][j]=INF;
            }
        }
        Floyd(n,dis);
        int ans=1;
        for(int i=1;i<=n;i++){
            for(int j=1;j<=n;j++){
                if(a[i][j]==1&&dis[i][j]%2==0) ans=0;  
                if(a[i][j]==0&&dis[i][j]%2==1) ans=0;
            }
        }
        if(ans==0) cout<<"NO"<<endl;
        else {
            cout<<"YES"<<endl;
            int cnt=0;
            for(int i=1;i<=n;i++){
                for(int j=i+1;j<=n;j++){
                    if(a[i][j]==1) cnt++;
                }
            }
            cout<<cnt<<endl;
            for(int i=1;i<=n;i++){
                for(int j=i+1;j<=n;j++){
                    if(a[i][j]==1) cout<<i<<" "<<j<<endl;
                }
            }
        }
    }
    return 0;
}

C. Excellent XOR Problem

题源：Gym - 104197E

题意：

询问是否能将给定数组划分为若干（至少两个）异或和不同的子数组，若答案是肯定的则给出构造；

思路：

由于题目的条件非常的弱，我们猜想可能不需要划分成很多子数组因为数量越多可能就约有可能出现相同的异或和，称题目划分异或和不同的子数组的操作为「合法的」；

尝试划分为两个，假如不能划分为两个，说明在任意位置分割原数组，左右两边的异或和都相等；

注意异或和的性质：$$A\wedge A=0,A\wedge 0=A$$; 换言之，若$$A\wedge B=C$$

  • 若$$A$$不等于$$B$$,那么$$C$$也不可能是$$0$$
  • 若$$C$$不等于0，$$A,B$$也不可能相等；

注意后面的性质实际上就是一种分拆方案，考虑数组全体的异或和$$sum$$,划分为两个如果是「非法的」，等价于$$sum=0$$;相反如果划分两个子数组是「合法的」，我们只需要取出第一个数和剩下的数就好了；

假如$$sum=0$$，我们退而求其次希望能够划分为三个子数组$$P,Q,R$$，我们找到原数组的前缀异或和，如果幸运地找到（第）一个非零的数$$x$$（如果找不到说明原数组和前缀异或和全都是零，答案就是否定的），假设在第$$i$$个位置非零，在位置小于$$i$$前缀异或和必定都是零,我们把前$$i$$个数加入$$P$$，$$P$$的异或和为$$x$$；

此时$$Q,R$$的全体的异或和也是$$x$$不为0，考虑到$$Q$$的异或和表现为从$$i+1$$开始的前缀异或和，从$$i+1$$开始更新持续加入当前位置的数，找到一个既不为0也不为$$x$$的，第$$i+1$$位置往后的前缀异或和就完成了（如果找不到，说明整个数组不是0就是$$x$$,那划分更多的数组也做不到「合法」，答案是否定的）；

当时被$$A$$卡爆了，题目是后面补的；

AC code：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
#define local
//#pragma GCC optimize(2)
#include<bits/stdc++.h>
#include<iostream>
using namespace std;
const int INF=1<<30;
const int maxn=200005;

void solution(){
    int n;
    cin>>n;
    vector<int> a(n+1);
    int fa=0;
    for(int i=1;i<=n;i++) cin>>a[i];
    for(int i=1;i<=n;i++) fa^=a[i];
    if(fa==0) {
        int i=0;
        for(i=1;i<=n;i++) if(a[i]!=0) break;
        if(i==n+1) {
            cout<<"NO"<<endl; 
            return;
        }
        else {
            int j=i+1;
            int x=a[i];
            int y=0;
            for(j=i+1;j<=n;j++){
                y^=a[j];
                if(y!=0&&y!=x) {
                    cout<<"YES"<<endl;
                    cout<<3<<endl;
                    cout<<1<<" "<<i<<endl;
                    cout<<i+1<<" "<<j<<endl;
                    cout<<j+1<<" "<<n<<endl;
                    return;
                }
            }
            if(j==n+1)  {
                cout<<"NO"<<endl;
                return ;
            }
        }

    }
    else {
        cout<<"YES"<<endl;
        cout<<2<<endl;
        cout<<1<<" "<<1<<endl;
        cout<<2<<" "<<n<<endl;
        return ;
    }
    return ;
};
int main ()
{
    //ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
    #ifdef local
    freopen("in.txt","r",stdin);
    freopen("out.txt","w",stdout);
    #endif // local

    int t;
    cin>>t;
    while(t--) solution();
    return 0;
}

D. Increasing Grid

题源：Gym - 104197I

题意：

给定一个初始已经填了若干个数的$$n\times m$$表格，求解能让这个表格从左上到右下严格递增，所有数不小于1，不超过$$n+m$$的填表方案数；

思路：

一眼每个数$$s[i][j]$$其实只有两种取值$$i+j-1,i+j$$,如果是前者那么他左上角的数一定全部都是取较小的数，如果是后者它右下角的数一定全部都是取较大的数，所以暂且不论没填的数，如果填的数不是这两个中的一个那肯定方案数就是0了（否则最左上角或者最右下角的数就要超出$$[1,n+m]$$的范围了），所以我么们让$$a[i][j]$$减去$$i+j-1$$,整张表就是$$-1，0，1$$表了；

按照这个思路我们先尽可能地填表，如果填表产生了矛盾说明不存在这样的方案；

现在还剩下一些没有填表的数，问题转化为找到这样一条从左下到右下的0-1分界线，这是非降路径计数问题，类似于$$Catalan$$数的求解，对还填着-1的格子$$dp$$即可；

一定要记得取模！

AC code：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
//#pragma GCC optimize(2)
#include<bits/stdc++.h>
#include<iostream>
using namespace std;
typedef long long ll;
const int mod=998244353;
void solution(){
    int n,m; 
    cin>>n>>m;
    vector<vector<int>> a(n+1,vector<int>(m+1));
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            cin>>a[i][j];
        }
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            if(a[i][j]==-1) continue;
            a[i][j]-=(i+j-1);
            if(a[i][j]!=0&&a[i][j]!=1) {
                cout<<0<<endl;
                return ;
            }
        }
    }
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            if(a[i][j]!=1) continue;
            if(i+1<=n){
                if(a[i+1][j]==0) {
                    cout<<0<<endl;
                    return ;
                }
                a[i+1][j]=1;
            }
            if(j+1<=m) {
                if(a[i][j+1]==0){
                    cout<<0<<endl;
                    return ;
                }
                a[i][j+1]=1;
            }
        }
    }
    for(int i=n;i>=1;i--){
        for(int j=m;j>=1;j--){
            if(a[i][j]!=0) continue;
            if(i-1>=1) {
                if(a[i-1][j]==1){
                    cout<<0<<endl;
                    return ;
                }
                a[i-1][j]=0;
            }
            if(j-1>=1){
                if(a[i][j-1]==1)
                {
                    cout<<0<<endl;
                    return ;
                }
            }
            a[i][j-1]=0;
        }
    }
    vector<vector<ll>> dp(n+1,vector<ll> (m+1));
    dp[n][0]=1;
    for(int i=n;i>=0;i--){
        for(int j=0;j<=m;j++){
            if(i+1<=n){
                if(j==0&&a[i+1][j+1]!=0) dp[i][j]+=dp[i+1][j];
                else if(j==m&&a[i+1][j]!=1) dp[i][j]+=dp[i+1][j];
                else if(j>0&&j<m&&a[i+1][j+1]!=0&&a[i+1][j]!=1) dp[i][j]+=dp[i+1][j];
                dp[i][j]%=mod;
            }
            if(j>0){
                if(i==n&&a[i][j]!=1) dp[i][j]+=dp[i][j-1];
                else if(i==0&&a[i+1][j]!=0) dp[i][j]+=dp[i][j-1];
                else if(i>0&&i<n&&a[i][j]!=1&&a[i+1][j]!=0)dp[i][j]+=dp[i][j-1];
                dp[i][j]%=mod;
            }
        }
    }
    cout<<dp[0][m]%mod<<endl;
}
int main ()
{
    //ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
    #ifdef local
    freopen("in.txt","r",stdin);
    freopen("out.txt","w",stdout);
    #endif // local

    int t;
    cin>>t;
    while(t--) solution();
    return 0;
}

E. Jewel of Data Structure Problems

题源：Gym - 104197J

题意：

给定$$[n]$$的置换和多组询问，回答每次交换操作后的序列最长奇子序列的长度；

思路：

  • 注意到如果序列是奇排列，那么那么最长的就是自己；
  • 如果序列是自然排列，那么是没有奇子序列的；
  • 如果序列是偶排列，如果我们能删去一个对逆序数贡献为奇数的数，那么删去这个数就可以得到奇排列；
  • 如果找不到这样的数，那么就要考虑删去更多的数，观察样例，猜想是否能删去两个数得到奇排列；
  • 我们有定理：对于长度为$$n$$的偶置换$$\phi:\phi_1,\phi_2,…,\phi_n$$,假设在$$\phi$$中下标小于$$k$$的,比$$\phi_k$$大的数有$$a_k$$个，比$$\phi_k$$小的数有$$k-1-a_k$$个；下标大于$$k$$的，比$$\phi_k$$小的数有$$b_k$$个,比$$\phi_k$$大的数有$$n-k-b_k$$个；
  • $$k-1-a_k+b_k=\phi_k-1,a_k+b_k\equiv\phi_k-k \ mod\ 2$$，如果序列删去$$a_k$$,逆序数减少$$(a_k+b_k)$$个，奇偶性取决于$$\phi_k-k$$;
  • 如果存在$$k$$,使得$$\phi_k-k$$为奇数，那么最长奇子序列长度为$$n-1$$;如果不存在，说明$$\phi_k-k$$全为偶数，删去两个数，由容斥原理，这两个数相关的逆序对要么都没计算要么计算两遍，要计算回来的话总逆序对数变化为奇数，那么序列最长奇子序列的长度为$%$$$n-2$$;

AC code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
#include<bits/stdc++.h>
#include<iostream>
using namespace std;
const int maxn=2e5+5;
 
class Segment_tree{
    public:
    int n;
    vector<int> tr;//这里维护的是和函数
 
    Segment_tree(int _n){//用参数
        int w=1;
        n=_n;
        while(w<n) w<<=1;
        w<<=1;tr.resize(w+1,0);
    }
    //更新线段树的原数组时
    //将数组下标为i的位置修改为x的单点更新,v是当前所在的树上结点位置
    void update(int v,int l,int r,int i,int x){
        if(l==r){
            tr[v]=x;
            return ;
        }
        int m=l+((r-l)>>1);
        if(i<=m) update(2*v,l,m,i,x);
        else update(2*v+1,m+1,r,i,x);
        tr[v]=tr[2*v]+tr[2*v+1];
    }
    //查询区间[l,r]和,当前在[x,y]以及v
    int get(int v,int x,int y,int l,int r){
        if(y<l||x>r)return 0;
        if(l<=x&&y<=r) return tr[v];
        int m=x+((y-x)>>1);
        return get(2*v,x,m,l,r)+get(2*v+1,m+1,y,l,r);
    }
 
};
 
int calc(int n,vector<int>&a){
    Segment_tree t=Segment_tree(n+1);
    int cnt=0;
    for(int i=1;i<=n;i++){
        if(a[i]<n) cnt+=t.get(1,1,n,a[i]+1,n);
        t.update(1,1,n,a[i],1);
    }
    return cnt; 
}
int main ()
{
    ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
    #ifdef local
    freopen("in.txt","r",stdin);
    freopen("out.txt","w",stdout);
    #endif // local
 
    int n,q;
    cin>>n>>q;
    int good=0 ,cnt=0;
    vector<int> p(n+1);
    for(int i=1;i<=n;i++) {
        cin>>p[i];
        if(p[i]==i) good++;
        if((p[i]-i)%2) cnt++; 
    }
    int sta=calc(n,p)%2;
    while(q--){
        sta^=1;
        int u,v;
        cin>>v>>u;
        if(p[v]==v) good--;
        if(p[u]==u) good--;
        if((p[v]-v)%2) cnt--;
        if((p[u]-u)%2) cnt--;
        swap(p[v],p[u]);
        if(p[v]==v) good++;
        if(p[u]==u) good++;
        if((p[v]-v)%2) cnt++;
        if((p[u]-u)%2) cnt++;
 
        if(good==n) cout<<-1<<endl;
        else {
            if(sta) cout<<n<<endl;
            else {
                if(cnt) cout<<n-1<<endl;
                else cout<<n-2<<endl;
            }
        }
    }
    return 0;
}

F. King of Swapping

题源：Gym - 104197K

题意：

给定长度为$$n$$的置换$$p$$,给定一系列由两个数$$a,b$$决定的操作：如果$$p_a>p_b$$,则可以交换$$p_a,p_b$$,判断这些操作的组合能否做到置换间的相互转化；

思路：

首先只要任意序列能做到与自然排列的相互转化，那么答案就是肯定的，否则是否定的；

我们考虑对操作的两个数连有向边，只需说明这个图是强连通的，也即这个图的强连通分量个数为$$1$$;

$$Tarjan$$缩点模板题；

注意可以不用对边重新初始化，合理卡常；

AC code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
#define local
//#pragma GCC optimize(2)
#include<bits/stdc++.h>
#include<iostream>
using namespace std;
const int maxn=400005;
class edge{
    public:
    int head;
    int to;
    int nxt;
}e[maxn];
void add(int u,int v,vector<int>&head,int&cnt){
    e[cnt].nxt=head[u];
    head[u]=cnt;
    e[cnt].head=u;
    e[cnt].to=v;
    cnt++;
}

int dep=0;
int instk[maxn];
stack<int> stk;
int sccnum=0;
void SCC(int x,vector<int>&head,vector<int>&dfn,vector<int>&low){
    if(sccnum>=2) return ;
    dfn[x]=low[x]=++dep;
    stk.push(x);
    instk[x]=1;
    for(int i=head[x];i;i=e[i].nxt){
        int y=e[i].to;
        if(!dfn[y]){
            SCC(y,head,dfn,low);
            if(sccnum>=2) break;
            low[x]=min(low[x],low[y]);
        }
        else if(instk[y])  low[x]=min(low[x],dfn[y]);
    }
    if(sccnum>=2) return ;
    if(low[x]==dfn[x]){
        sccnum++;
        if(sccnum>=2) return ;
        while(stk.top()!=x){
            int y=stk.top();
            instk[y]=0;
            stk.pop();
        }
        instk[x]=0;
        stk.pop();
    }
    return ;
}
void solution(){
    int n,m;
    scanf("%d%d",&n,&m);
    vector<int> head(n+1);
    vector<int> dfn(n+1);
    vector<int> low(n+1);
    //memset(e,0,sizeof(e));
    dep=0;sccnum=0;
    int cnt=1;
    for(int i=1;i<=m;i++){
        int u,v;
        scanf("%d%d",&u,&v);
        add(u,v,head,cnt);
    }
    for(int i=1;i<=n;i++) if(!dfn[i]&&sccnum<=1) SCC(i,head,dfn,low);
    if(sccnum==1) puts("YES");
    else puts("NO");
    return;
}
int main ()
{
    //ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
    #ifdef local
    freopen("in.txt","r",stdin);
    freopen("out.txt","w",stdout);
    #endif // local

    int t;
    scanf("%d",&t);
    while(t--) solution();
    return 0;
}

G. Digital Path

题源：Gym - 103466C

题意：

搜索方格中有多少条依次递增$$1$$的、极长的（不能在头尾拓展的），每个格子的下一格子是相邻的，长度至少为$$4$$的路径；

思路：

考虑暴力$$DFS$$;

每次为开头的格子打上标记，每次进入相邻的合法的格子，回溯的时候在相应长度计数；

注意$$-1$$是可以走的，不要被样例误导；

AC code：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
//#pragma GCC optimize(2)
#include<bits/stdc++.h>
#include<iostream>
using namespace std;
typedef long long ll;
const ll mod=1000000007;
const int maxn=1005;
class Node{
    public:
    int w;
    int x;
    int y;
    Node(){}
    Node(int a, int b, int c){w=a;x=b;y=c;};
    bool operator < (const Node&obj)const {
        return w<obj.w;
    };
};
Node v[1000005];
int tab[maxn][maxn];
bool vis[maxn][maxn];
int sp1[5]={0,0,1,-1};
int sp2[5]={1,-1,0,0};
ll dp[maxn][maxn][5];
void dfs(int x,int y,int w,int n,int m){
    vis[x][y]=true;
    bool stop=true;
    for(int i=0;i<4;i++){
        int tx=x+sp1[i];
        int ty=y+sp2[i];
        if(tx<1||tx>n||ty<1||ty>m||tab[tx][ty]!=1+tab[x][y]) continue;
        if(!vis[tx][ty]) dfs(tx,ty,w+1,n,m);
        stop=false;
        dp[x][y][4]+=dp[tx][ty][3]+dp[tx][ty][4];
        dp[x][y][4]%=mod;
        dp[x][y][3]+=dp[tx][ty][2];
        dp[x][y][3]%=mod;
        dp[x][y][2]+=dp[tx][ty][1];
        dp[x][y][2]%=mod;
    }
    if(stop) dp[x][y][1]=1; 
    return ;
}
int main ()
{
    ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
    #ifdef local
    freopen("in.txt","r",stdin);
    freopen("out.txt","w",stdout);
    #endif // local
 
    int n,m;
    cin>>n>>m;
    memset(tab,0,sizeof(tab));
    int cnt=0;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            cin>>tab[i][j];
            Node p(tab[i][j],i,j);
            v[cnt++]=p;
        }
    }
    sort(v,v+cnt);
    memset(vis,false,sizeof(vis));
    ll ans=0;
    for(int i=0;i<cnt;i++){
        int x=v[i].x;
        int y=v[i].y;
        int w=v[i].w;
        if(!vis[x][y]) {
            dfs(x,y,w,n,m);
            ans+=dp[x][y][4];
            ans%=mod;
        }
    }
    cout<<ans<<endl;
    return 0;
}

H. A Hard Problem

题源：Gym - 103466A

题意：

在$$n$$个数中最多找到多少个数，使得任意两个数其中一个不是另一个的因数；

思路：

抽屉原理水题，答案是约一半的数，构造是最大的那一半数；

每个抽屉是所有最大奇因数相同的数的集合，超过一半肯定会有两个数在一个抽屉中，这两个数其中一个是另一个的因数；

在训练赛的时候没机会看榜，水题都没过；

AC code：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
//#pragma GCC optimize(2)
#include<bits/stdc++.h>
#include<iostream>
using namespace std;

int main ()
{
    //ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
    #ifdef local
    freopen("in.txt","r",stdin);
    freopen("out.txt","w",stdout);
    #endif // local

    int t;
    cin>>t;
    while(t--){
        int n;
        cin>>n;
        cout<<(n+3)/2<<endl;
    }
    return 0;
}

Remark

训练赛的时候没时间补题，被刷了后才全部补上；

Posted on

B： 我承认阁下的字符串匹配很强

题意：

含有通配字符串的匹配问题;

思路:

采取暴力搜索文本串的思路；

假设当前搜索的位置为$$dfs(pos)$$,比较该位置往后的$$patlen$$个位置,观察是否能匹配，若能，便右移$$next$$个位置，若不能便右移一个位置，注意右移$$next$$个位置未必比右移一个位置更优，转移方程为$$dfs(pos)=max(dfs(pos+1),dfs(pos+next)+1)$$；

$$next$$是指模式串最长的前缀等于后缀的长度；

C： Necklace

题意：

找到字符串$$T$$所在的循环群字典序最小元；

思路：

循环群每一个元实际上都可以用原串的一个下标表示，因此无需复制；

比较不需要全串比较，只需要跳过前面相同的部分，比较第一个不同的字母即可；

暴力枚举所有的字符串，保持$$best$$的位置的更新；

C：Trap-Sirrom-Tunk

题意：

给定模式串与文本串，求解文本串的匹配次数；

思路：

$$KMP$$算法模板题；

找到模式串的$$next$$数组，考虑从前往后暴力遍历匹配，如果匹配失败则右移$$next$$个位置，否则答案自增1；

J: 数据攻防1

题意：

给定若干模式串，找到在文本串中出现的次数；

思路：

$$AC$$自动机模板题；

将每个模式串插入$$trie$$中，建立$$fail$$指针，遍历文本串，每次经过模式串在$$trie$$

树打的标记便自增1；

L： Obsession

题意：

在字符串末尾增加字符使得原串成为周期的；

思路：

利用$$KMP$$算法找到$$next$$数组，并且利用数组找到最佳的周期，如果原串是周期的倍数但是不等于周期，说明答案为0，否则，将原串补为最近的周期的倍数即可；

Posted on

A： 喜闻乐见的题

题意：

给定两圆，以其中一个圆内为中心作正方形完全在这个圆内的条件，正方形完全在另一个圆的条件概率；

思路：

由条件概率公式$$P(B|A)=\frac{P(AB)}{P(A)}$$,我们只需要求出$$P(AB)$$和$$P(A)$$即可；

$$P(A)$$的求解：正方形中心可行域为以$$A$$为圆心，$$\frac{\sqrt{4r_1^2-d^2}-d}{2}$$为半径的圆，输入保证这个半径长度不为$$0$$；

$$P(BA)$$的求解：由以上的分析，正方形的中心也在以$$B$$为圆心，$$\frac{\sqrt{4r_2^2-d^2}-d}{2}$$的圆内（注意输入没有保证，要特判不存在的情形），因此正方形的中心可行域为两圆的相交区域，问题转化为两圆相交面积问题模板；

两圆面积交问题：

  • 如果两圆相离、外切、内切或者内含，那么他们的面积交为0；

  • 如果两圆相交，可以通过容斥原理转化为两个扇形面积减去两个三角形的面积；

  • 由于三角形的顶点为两圆交点并不方便求解，可以考虑采用$$Heron$$公式；

B: 此曲一响，_______________

题意：

给定多边形$$Polygon$$和点$$T，S$$,求多边形内部到$$S$$的距离不超过到点$$T$$的距离的$$k$$倍的所有点构成区域面积；

思路：

到两定点比值一定的轨迹构成$$Apollonius$$圆；

其中，两定点和与定点共线的直径的两个对径点共同构成调和点列，通过这个性质可以快速求出$$Apollonius$$圆的半径和圆心（注意题目输入保证是不会让圆退化为中垂线的）；

问题转化为多边形与圆面积交模板：

  • 以圆的圆心为视点，对多边形作三角剖分；

  • 一点为圆心的三角形与圆面积交分为四种情况：

    • 所对线段两点完全在圆内，此时面积交为整个三角形；

    • 如果线段两端点有以一个在圆外一个在圆内，那么面积交为一个三角形和一个扇形

    • 如果线段两端点两个端点均在圆外且线段与圆没有交点（或相切），那么面积交为一个扇形；

    • 如果线段两端点两个端点均在圆外且线段与圆有交点，那么面积交为一个三角形加两个

      扇形；

    • 注意这里涉及反三角函数的转化，如果出现点重合的情况一定要特判为0，否则可能会出现$$nan$$

  • 整个多边形与圆面积交为各个三角形与圆面积交的有向和；

E: 麦田怪圈II

题意：

求出内外切于两圆之间的前$$n$$个最大圆面积和；

思路：

以两圆切点为反演中心，$$1$$为反演半径作反演变换；

两圆化成平行两直线，要求的$$n$$个圆直径均为两平行直线的距离，由反演变化距离公式以及圆幂定理，设反演中心$$I$$和左（右）手第$$k$$个圆圆心连线交点为$$C,D$$，那么反演变换前该圆的直径$$2r[k]=C’D’=\frac{CD}{IC \cdot ID}=\frac{(r_2-r_1)r_1r_2}{k^2(r_2-r_1)^2+r_1r_2}$$，面积总和即为$$\sum_{k=1}^{n}\pi[k/2][k/2]$$；

注意这里$$k,n$$应该要开long long 否则整形的精度将会溢出导致半径为负；

F: 麦田怪圈III

题意：

给定$$n$$个圆，判断原点是否在它们的「包围圈」内，所谓「包围圈」是指由它们的本身和两两外公切线所围成最大的凸集；

思路：

不难发现原点到各个圆的两条公切线是问题关键，（当然如果没有的话问题答案即为YES），对每一条切线的极角排序（无需分象限），如果有相邻的极角之差超过$$\pi$$，那么答案便是NO；

第$$i$$个圆的两条切线的极角$$\theta=atan2(y_i,x_i)\pm asin(\frac{r_i}{\sqrt{x_i^2+y_i^2}})$$;

I: 过马路

题意：

求运动的多边形和动点不相遇的最长持续时间；

思路：

（题解的正确性存疑，因为本人$$hack$$过自己的几组边界数据但是提交却出现$$AC$$的情况，本人也认为思路不完全正确）；

考虑转化运动参考系，将多边形当作惯性系，那么动点$$x$$向速度恒为$$v$$,$$y$$向速度不大于$$u$$,如果初始状态多边形的点全部都在射线$$y=\frac{ux}{v}$$的一侧，那么动点无需等待全力过马路即可，时间为$$w/u$$,否则等待一段时间，这段时间是每个点作方向为$$(v,u)$$的「切线」最右侧所代表的时间，换言之，$$T=max_{1\le i\le n}(\frac{x}{v}-\frac{y}{u})$$，再全速前进即可；

N：回转数

题意：

求给定点关于给定多边形的回转数；

思路：

为降低时间开销不考虑极角排序做法；

遍历每一条边，判断边$$uv$$与点$$a$$的相对位置关系；

回转数自增当且仅当

  • $$(v-u)\times(a-u)>0$$
  • $$u.y\le a.y$$
  • $$a.y<v.y$$

回转数自减当且仅当

  • $$(v-u)\times(a-u)<0$$
  • $$u.y\ge a.y$$
  • $$a.y>v.y$$

S: 兔儿爷（Simple Version）

题意：

判断点是否在三角形的内部；

思路：

本题是$$T$$题的$$n=3$$ 的版本；

T: 兔儿爷（Easy Version）

题意：

判断点是否在多边形的内部（多边形可能会退化，也不一定是凸的）；

思路：

本题由两个模板组成；

  • $$Graham$$算法求给定点集的凸包

    • 选定二维偏序最小者为极点
    • 剩余的点作极角排序
    • 维护单调栈，逆时针第一条边入栈，若新加入的点在栈顶边的右侧则出栈，否则直接入栈，始终保证栈内至少有两个点（一条边）；

  • 二分极角序判断点是否在凸多边形内

    • 选取二维偏序最小者为极点
    • 三角剖分多边形，二分对角线位置，判断在最大在何处对角线的左侧
    • 判断是否在两条对角线夹边内部

  • 注意事项：

    1. 退化情况包括$$n=1,n=2$$
    2. 点在对角线或者一边的延长线上，此时不能算作在多边形的内部；

Posted on

一个寒冷的秋夜。一个男人裹着一件外套，正沿着一条灰色的街道快速行走。这是乌拉尔国立大学ACM俱乐部的传统守护者。细雨和沉闷的天空总是让他怀念。我们再来一次，传统守护者正在带回遥远过去的记忆，当时乌拉尔联邦大学还不存在，Team.GOV 的故事才刚刚开始。的确，这个故事值得为后人保存。然而，细节正在从守护者的脑海中溜走，他似乎需要一个档案。屠格涅瓦街4号六楼，是数学和力学系，守护者本人很久以前就一直在学习。长长的走廊，地板上的狭窄灯条，黑暗的角落，最终是一个带有ACM档案的办公室。门将打开门，发现自己处于狭窄之中
房间有许多架子。数十个盒子和成堆的纸张被倾倒在墙壁附近。在一个盒子上，三个字母闪闪发光
与黄金 - 政府。守门员走到箱子前，抽出一个沉重的文档，打开
它。在右上角的第一页上，有一张微笑的年轻人的照片，他留着卷发，下标：“瓦迪克·坎托罗夫，Team.GOV 的永久船长”。瓦迪克进入大学后，他玩了几个花样，进入了亚历克斯E.和米莎的半准备团队。Alex E.是一个聪明的进程员，即使他是一个学者，所以困扰着ACM的老前辈。因此，Alex E.准备将团队命名为“警报”。因此，瓦迪克的ACM生涯开始了。该团队存在了一年。第一场战斗是乌拉尔SU锦标赛，警报只获得了第五名，减轻了老兵的恐惧。下一个比赛是ACM ICPC次区域比赛。球队表现稍好一些，在所有球队中排名第七
来自乌拉尔地区，来自乌拉尔SU的团队中排名第三。警报成为乌拉尔SU历史上第三支有资格参加圣彼得堡地区比赛的新生团队。不幸的是，在地区比赛中，该队获得了第86名，打破了乌拉尔SU队最低排名的记录。这对球队来说是一个沉重的打击。必须做出选择：大量练习，退出编程竞赛，或者继续表现不佳。
放回决定，球队参加了乌拉尔锦标赛，在所有球队中排名第19，在乌拉尔SU球队中排名第5。就在那一刻，很明显阵容必须改变。然而，在乌拉尔锦标赛之前，警报已经申请了鞑靼斯坦锦标赛，球队的决赛在那里举行。该团队甚至无法解决一半的问题，也没有进入最好的十个团队（第 11 名）。在火车上返回的路上，决定米莎必须退出团队。在新赛季，球队需要一个新名字。序言到此完成，故事
Team.GOV 开始了。该团队由两名经验不足但更不成功的成员组成。定义了一个新名称 - Team.GOV。经过长时间的考虑，瓦迪克发现团队错过了一位强大的数学家。萨沙曾是瓦迪克的高中朋友，她被选中担任这个角色。随着萨沙的出现，所有人都觉得一切都会顺利进行。乌拉尔SU锦标赛的时间到了，2008年秋天，大学第二年。在不清楚的情况下，萨沙没有参加比赛，但即使在这种情况下，Team.GOV 也是第二好的
乌拉尔苏团队。一年的经验得到了回报！萨沙确实参加了次区域比赛，但球队只获得了第14名，没有资格参加区域比赛。幸运的是，乌拉尔苏作为次区域比赛的主办方，有权额外派出一支队伍参加区域比赛。经过长时间的谈判，Team.GOV 可以参加地区比赛，但突然
阵容的变化——伊万·替换结果是富有成效的 - 第76位（Alarm的成就为10）。回国后，伊万B.找到了另一支球队，因此Team.GOV不得不再次修复阵容。尼基塔被邀请作为乌拉尔锦标赛的第三名球员。在资格赛中，瓦迪克、尼基塔和亚历克斯·E.表现出色：球队在乌拉尔队中排名第二。真是惊人的成功！非常热情的瓦迪克和尼基塔来到了乌拉尔锦标赛。出于某种奇怪的原因，亚历克斯·没来。这支球队的表现又一次非常糟糕——在所有球队中排名第25位，在乌拉尔SU队中排名第5。尼基塔对这种态度并不满意，Team.GOV 只剩下两个球员
再次——亚历克斯E.和瓦迪克。真是诅咒！团队开始寻找第三名球员。下一个赛季来了——瓦迪克进入乌拉尔大学已经两年了。寻找第三名队友的工作顺利完成。高年级学生费多尔非常有经验，从高中9年级开始练习。光明的未来摆在团队面前。诅咒结束了 andTeam.GOV 用同样的阵容打了三场正式比赛。该团队在次区域比赛中获得第12名，安全晋级区域赛，然后在乌拉尔SU锦标赛中获得第三名。
在圣彼得堡举行的地区比赛产生了文凭和第61名，比前一次高出15名
年的位置。从圣彼得堡回来后，Team.GOV 参加了ACM ICPC的独特比赛
退伍军人和现任团队——世代之战。可悲的是，Alex E.不能来，但团队认为
伊万·
对比赛的态度——瓦迪克开始寻找替代者。尼基塔愉快地接受了一次邀请
他听说亚历克斯E.退出了球队。他回到 Team.GOV 后的第一场比赛是资格赛
乌拉尔锦标赛。突然间，瓦迪克在欧洲有了一些紧急的事情，于是费多尔和尼基塔
没有他就参加了。他们表现得很好，解决了和领导者一样多的问题。如
结果，球队获得了第三名，并获得了乌拉尔锦标赛的资格。
乌拉尔锦标赛带来了新的悲伤：在所有团队中排名第25位，在乌拉尔SU团队中排名第4。
费多尔和尼基塔无法控制住神经，瓦迪克不得不重新寻找新的队友。
大学的第四年，也是最后一年。瓦迪克想结束他的ACM职业生涯，他需要
一个新的团队。退伍军人建议带年轻有前途的丹，瓦迪克进行了一个小测试，
登被带走了。距离乌拉尔SU锦标赛只剩下几天了，几乎所有的球队
成立时，瓦迪克还在回答他永恒的问题——从哪里得到第三个队员？
无意中，他发现Egor在之前的团队解散后正在寻找新的团队。新
Team.GOV 的阵容诞生了
在乌拉尔SU锦标赛上，Team.GOV 再次失败，仅获得第5名。次区域
比赛也不成功——在所有团队中排名第 9，在乌拉尔 SU 团队中排名第 4。乌拉尔
SU得到了一个延长的配额，Team.GOV 又要去圣彼得堡了。圣彼得堡之前
Team.GOV 需要一个认真的练习课程。全西伯利亚奥林匹克运动会是一个完美的镜头。Team.GOV 去了
到新西伯利亚，再次发现他们有多弱：所有球队第 39 名，最差
乌拉尔SU团队的表现。因此，这些家伙带着很棒的休闲计划出发前往圣彼得堡。嗯，
参与不亚于胜利！
在区域比赛中，令人惊讶的是教练，团队。GOV在前四题中打了五道题
小时，排名相当高。赛后，教练们发现球队不仅得分
第六个问题，也是第七个问题。结果 — 第 26 名（去年排名第 35 位）和 a
二级文凭。Team.GOV 终于获得了成功和荣耀。回家的路就在前方
在春天，Team.GOV 传统上分手了。瓦迪克想做一些花哨的事情，这是他的最后一次
毕竟是比赛。瓦迪克邀请了他的中国女友小红。第三个受邀的队友，不幸的是，
没有来，所以在最后一刻，瓦迪克带着维塔利（ACM ICPC世界总决赛的奖牌获得者）换
乌拉尔锦标赛前的游戏锦标赛。不幸的是，维塔利无法参加
主比，于是瓦迪克把萨沙当成了老朋友。这是 Team.GOV 的最后一场比赛。
传统守护者挠了挠头：在多少次警报/Team.GOV 比赛中，每支队伍都有
会员参与？瓦迪克一直说米莎是零号成员，因为他玩过
在球队得名之前的 Team.GOV。瓦迪克确实是第一名球员。有一个棘手的案例
和维塔利：当然，他没有参加过任何 Team.GOV 比赛，游戏锦标赛不应该
数。但他绝对配得上 Team.GOV 的历史，因为他是一个奖项
世界总决赛的获胜者和一般有价值的球员。
传统守护者一丝不苟地列出了 Team.GOV 的所有成员。（米莎 — 0， 瓦迪克 — 1， 亚历克斯
E. — 2， 萨沙 — 3， 伊万 B. — 4， 尼基塔 — 5， 费多尔 — 6， 伊万 K. — 7， 登 — 8， 叶戈尔 — 9， 小红 —
10，维塔利 — 11）。他数了数，零号已经打了5次（因为正好5场比赛是
由警报器饰演）。第一名参加了21场比赛。
你以为是这样吗？从乌拉尔联邦大学毕业后，瓦迪克搬到了巴黎，并
三年后再次参加ACM ICPC比赛。瓦迪克和他的两个队友（蒂莫西
和亚历山大）前往瓦伦西亚参加SWERC地区比赛。他们取得的所有成就
解决了两个问题，达到了第29位。这让ACM ICPC职业生涯的瓦迪克悲哀地结束了，
这是他最后一次参加地区比赛。
附注：提摩太和亚历山大的人数分别是12和13。
唯一的一行包含一个从 0 到 13 的整数 — Team.GOV 玩家的数量。
输出给定成员在传奇团队中参加的比赛次数。所有比赛必须
算了，但乌拉尔锦标赛之前的比赛锦标赛

Posted on

阿哲是个恶霸，无恶不作，喜欢欺负弱小。他的队友们被虐待了很久。最后，他们决定不再忍受自己的好友，在恶霸的紧追下逃往数字村。由于地形复杂，而且有相当数量的数字路径交错，他们不可能轻易被捕。

尽快熟悉地形对这些无辜者摆脱欺凌威胁非常重要。现在，他们需要做的就是清点数字村中的数字路径数量。

为了简化问题，我们将数字村抽象成一个网格，网格的 $n$行和 $m$列由整数填充。数字路径是网格中满足以下条件的连续行走：

  • 行走中相邻的方格共享一条公共边；
  • 行走是最大的，不能扩展；
  • 至少包含四个方格；
  • 从一端到另一端，任意两个相邻方格的数值增量正好为 1。

下面我们举几个例子。

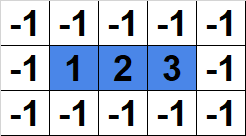
图 1：无效路径。

图 1 中的路径是无效的，因为它的长度小于 $4$。

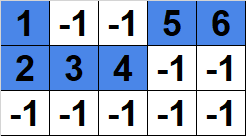
图 2：无效路径。

图 2 中的路径是无效的，因为它不连续。

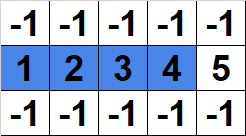
图 3：无效路径。

图 3 中的路径是无效的，因为它可以进一步扩展。

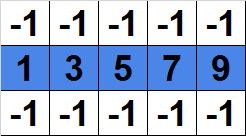
图 4：无效路径。

图 4 中的路径也是无效的，因为路径中的值并没有严格地增加 1。

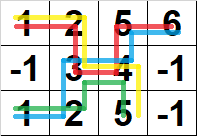
图 5：所有有效路径。

数字路径可能部分重叠。在图 5 中，有 $4$字路径用不同颜色标出。

0%