README

Posted on 2025-05-01

FileTree

myapriori
├─ .idea
│  ├─ encodings.xml
│  ├─ inspectionProfiles
│  │  ├─ profiles_settings.xml
│  │  └─ Project_Default.xml
│  ├─ misc.xml
│  ├─ modules.xml
│  ├─ myapriori.iml
│  ├─ vcs.xml
│  └─ workspace.xml
├─ Apriori
│  ├─ Apriori.py
│  ├─ __init__.py
│  └─ __pycache__
│     ├─ Apriori.cpython-311.pyc
│     └─ __init__.cpython-311.pyc
├─ docs
│  ├─ README.md
│  └─ 第三章：关联模式挖掘.md
├─ README.md
├─ scripts
│  └─ getRelativePath.py
└─ tests
   ├─ data
   │  ├─ input.txt
   │  └─ output.txt
   └─ test_1.py

Usage

在/docs中有关于Apriori算法的介绍
关于ide

vscode：在/Apriori中运行Apriori.py
pycharm: 在/test运行test_1.py

Untitled

Posted on 2025-05-01 Edited on 2023-10-28

基于Multisim的方波-三角波-正弦波-锯齿波函数发生器电子电路仿真项目设计

author: 谢卿云计算机科学与工程学院（网络安全学院）计算机科学与技术（“互联网+”复合型精英人才双学位培养计划）专业 2022010910017
date：26th，June，2023

摘要

函数信号发生器是在电子电路设计领域和设备检测领域应用极广，本项目利用基础的电子电路元件（电阻，电容，电位器，理想开关，直流稳压电源，运算放大器，二极管，稳压管等），通过对信号发生的基本原理与结构进行了分析，设计了简易的方波-三角波-正弦波-锯齿波函数信号发生器：由各个直流稳压电源提供运算放大器的供电电压，利用文氏正弦型振荡电路产生正弦波，滞回比较器和同相比例放大器产生方波，在此基础上，利用积分放大器产生三角波以及利用电位器和二极管产生了锯齿波；本实验的全部结果均由软件Multisim14.2仿真完成。

关键词：文氏正弦型振荡电路，滞回比较器，积分放大器，Multisim14.2。

Abstract：

Function signal generator is widely used in the field of electronic circuit design and equipment detection. This project uses basic electronic circuit components (resistors, capacitors, potentiometers, ideal switches, DC regulated power supplies, operational amplifiers, diodes, regulated tubes, etc.) to analyze the basic principle and structure of signal generation. A simple square-wave-triangular-sine-wave-sawtooth function signal generator is designed: the power supply voltage of the operational amplifier is provided by each DC voltage regulator, sinusoidal oscillation circuit is used to generate sinusoidal wave, hysteresis comparator and multiplication amplifier to generate square wave, and on this basis, triangular wave is generated by integrating amplifier and sawtooth wave is generated by potentiometer and diode. All the results of this experiment were simulated by Multisim14.2 software.

Key words: sinusoidal oscillation circuit, hysteresis comparator, integrated amplifier, Multisim14.2.

第一章：前言、课程设计任务与要求

函数信号发生器是一种信号发生装置，能产生某些特定的周期性时间函数波形信号，频率范围可从几个微赫到几十兆赫。除供通信、仪表和自动控制系统测试用外，还广泛用于其他非电测量领域，现代工业生产的函数发生器多采用集成电路。为进一步掌握电路基本理论与增强实验实践能力，本项目采用由集成运算放大器等分立式元件共同组成简易的方波-正弦波-三角波-锯齿波。

通过对电路分析与电子电路课程的学习，以及在电子电路实验的实践操作中，本设计应达到的任务与要求为：

输出波形频率范围为0.02Hz~20kHz且连续可调；
正弦波幅值为±2V；
方波幅值为2V，占空比可调；
三角波峰-峰值为2V；
锯齿波峰-峰值为2V；
设计电路所需的直流电源可用实验室电源。

第二章：电路设计原理

2.1 正弦波产生电路工作原理

正弦波产生电路是一种振荡模型，满足巴克豪森稳定性准则：电子振荡器系统信号由输入到输出再反馈到输入的相差为360°，且增益为1，为振荡器振荡的必要条件。我们注意到电路启动时具有频率丰富的热白噪声，我们如果在放大电路中引入正反馈调节，在所有频率的信号都得到放大，在通过滤波相关的元件筛选出针对特定频率的信号，与原来同相位的信号叠加，重新输入至放大器中往复，最终形成振荡的信号。因此，一个正弦产生电路一般包括：放大电路，正反馈网络，选频网络，非线性环节。

2.1.1 产生正弦振荡的条件：

以热白噪声作为输入信号，要求输出频率一定且可调、一定幅值的信号；
引入的正反馈调节且振荡频率可控；
在产生稳定的振荡后，要求电路输出量自维持，也即：
$$
\dot{A}\dot{F}=1\Longleftrightarrow \left | \dot{A}\dot{F} \right | =1,\varphi _{A}+\varphi _{F}=2n\pi
$$
其中，前者被称为幅值平衡条件，后者被称为相位平衡条件；
信号幅值有从小到大直至稳幅的变化过程，必须满足起振条件，也即：
$$
\left | \dot{A}\dot{F} \right | >1
$$

2.1.2 基本组成部分及其作用

放大电路：放大幅值；
正反馈网络：满足相位平衡条件；
选频网络：具有变化的电位器，确定保证产生正弦振荡的信号；
非线性环节：稳幅；
同向比例放大电路：使得幅值达到要求。

2.1.3 文氏桥正弦型振荡电路及分析

用同相比例运算电路作放大电路，以RC串并联网络为选频网络和正反馈网络、并引入电压串联负反馈，两个网络构成桥路，一对顶点作为输出电压，一对顶点作为放大电路的净输入电压，就构成文氏桥振荡器。如图2.1.3.1所示：

$$
{\dot{U} {+}} =\frac{R//\frac{1}{j\omega C} }{R+\frac{1}{j\omega C}+R//\frac{1}{j\omega C} } \dot{U}{o}

=\frac{\dot{U}_{o}}{3+j(\omega RC-\frac{1}{\omega RC} )}
$$

$$
\dot{U} {-} =\frac{R{1} \dot{U} {o} }{R{1}+R_{F}}
$$

$$
\dot{A}\dot{F}=1\ \Longleftrightarrow \ 3+j(\omega RC-\frac{1}{\omega RC} )=\frac{R_{1}+R_{F}}{R_{1}}
\Longleftrightarrow \ \omega =\frac{1}{RC},R_{F}=2R_{1}
$$

2.2 方波产生电路工作原理

方波是一种典型的非正弦波，它有且只有高电平和低电平两个值，是数字逻辑信号的重要的部分，要求两种状态的相互自动转化，输出的信号必须以某种方式反馈于它的输入，以某种周期进行交替变化，电路中必须要有相应的延迟环节，因而使用滞回比较器和RC回路自充放电作为延迟环节来模拟方波信号的发生。

2.2.1 产生方波的条件

集成运算工作在非线性区；
正反馈调节；
输出电压限幅。

2.2.2 基本组成部分及作用

滞回比较电路：正反馈；
一阶RC回路：延迟环节，进行电压的跳变；
调节占空比环节：调节占空比。

2.2.3 滞回比较器电路及分析

输入电压和输出电压之间的反馈完成，依赖于电容的充放电过程，如图2.2.3.1

$$
when \ U_{o}=U_{Z} ,U_{+}=\frac{R_{1}}{R_{1}+R_{2}}U_{o},\ C \ is \ incharging
$$

$$
\
until \ U_{C} =U_{-}>U_{+},U_{o}=-U_{Z}
$$

$$
when \ incharging,U_{C}=U_{Z}-\frac{2R_{1}+R_{2}}{R_{1}+R_{2}}e^{-\frac{t}{RC}}
$$

$$
until \ U_{C}=\frac{R_{1}}{R_{1}+R_{2}}U_{Z},jump,t=2R_{3}Cln(1+\frac{2R_{1}}{R_{2}})
$$

$$
changing \ R_{3},\ then \ chaging \ duty\ ratio.
$$

2.3 三角波产生电路工作原理

从数学关系不难看出，将方波函数按照区间积分可以得到三角波函数，因此只需要在方波产生的电路基础上串联一个积分运放器。

2.3.1 基本组成部分及作用

方波产生电路；
积分放大器；
调频环节。

2.3.2 串联分析

注意电阻调频电阻R1的位置与Uo相连，如图2.3.2.1所示：

2.4 锯齿波产生电路工作原理

锯齿波是更为一般的三角波，我们只需要改变三角波的占空比即可得到锯齿波。

2.4.1 基本组成部分及作用

三角波产生电路；
调节占空比环节。

2.4.2 基本组成电路

注意调节占空比环节的接法，如图2.4.2.1所示：

第三章：Multisim仿真项目实验数据与方法记录

3.1 正弦波发生实验数据和方法

完整的仿真电路图如图3.1.1所示

其中，闭合开关，先将R4调节100%，以满足起振条件，观察到XSC2变化至稳幅状态，再调回R4至40%不变，可以观察到XSC1即为满足条件的正弦信号，调节R1，R6可以更改信号频率，更改R2可以更改信号幅值，仿真数据如图3.1.2所示

3.2 方波发生实验数据与方法

完整的仿真电路图如图3.2.1所示

滑动S2，S4所在的电位器，可以调节方波占空比，实验数据如图3.2.2所示：

3.3 三角波发生实验数据与方法

完整的仿真电路图如图3.3.1所示

调节合适R17和外接电源电压的值可以得到符合要求的三角波，如图3.3.2所示：

3.4 锯齿波发生实验数据与方法

完整的仿真电路图如3.4.1所示

调节S1，S4所在电位器可以改变占空比，实验数据如图3.4.2所示：

第四章：总结与体会

通过本次仿真实验，我对软件Multisim有了更深层次的认识，掌握熟练运用并搭建合适的模型解决实际问题的能力，也希望仿真技术能为以后的学习工作带来更多遍利；
通过对掌握的理论知识加上仿真实验带来的实践思考，我对电子电路学科有了进一步的了解，系统地总结了一部分知识，对将来信息学科的学习大有裨益；
通过对文字排版和内容规划，我对markdown这一语言有了更加熟练的应用；
但本次仿真项目仍然存在部分遗憾的情况:比如改变三角波中R17右端的位置至R3右端，则不能得出令人满意的仿真结果，具体原因有待进一步的考察。

Multisim元器件中文与英文对照表

Posted on 2025-05-01

Multisim元器件中文与英文对照表

1。Source库：包括电源、信号电压源、信号电流源、可控电压源、可控电流源、函数控制器件 6个类。

2。BASIC库：包含基础元件，如电阻、电容、电感、二极管、三极管、开关等；

3。Diodes：二极管库，包含普通二极管、齐纳二极管、二极管桥、变容二极管、 PIN

二极管、发光二极管等。

4。Transisitor库：三极管库，包含 NPN、PNP、达林顿管、IGBT、MOS管、场效应管、可控硅等；

5。Analog库：模拟器件库，包括运放、滤波器、比较器、模拟开关等模拟器件

6。TTL库：包含 TTL型数字电路如74007404 等门BJT电路。

7。COMS库：COMS型数字电路如74HC0074HC04 等MOS管电路。

8。MCUModel ： MCU模型，Multisim 的单片机模型比较少，只有 8051PIC16 的少数模型和一些 ROMRAM 等

9。AdvancePeriphearls库：外围器件库，包含键盘、 LCD 、和一个显示终端的模型。

10。MIXCDigital ：混合数字电路库，包含 DSP、CPLD、FPGA、PLD、单片机-微控制器、存储器件、一些接口电路等数字器件。

11。Mixed：混合库，包含定时器、 AC/DA 转换芯片、模拟开关、震荡器等；

12。Indicators：指示器库，包含电压表、电流表、探针、蜂鸣器、灯、数码管等等显示器件。

13。Power：电源库，包含保险丝、稳压器、电压抑制、隔离电源等

14。Misc：混合库，包含晶振、电子管、滤波器、 MOS驱动、和其他一些器件等

15。RF：RF库，包含一些 RF器件，如高频电容电感、高频三极管等

16。Elector Mechinical：电子机械器件库，包含传感开关、机械开关、继电器、电机等。。

Proteus元件名称对照 1

元件名称中文名说明

7407驱动门

1N914二极管

74Ls00与非门

74LS04非门

74LS08与门

74LS390TTL 双十进制计数器

7SEG4 针BCD-LED 输出从0-9 对应于4根线的BCD码

7SEG3-8译码器电路 BCD-7SEG[size=+0]转换电路ALTERNATOR 交流发电机

AMMETER-MILLImA 安培计

AND 与门

DCPOWER 电池/电池组

BUS 总线

CAP电容

CAPACITOR 电容器

CLOCK 时钟信号源

CRYSTAL 晶振

D-FLIPFLOPD 触发器

FUSE保险丝

GROUND 地

LAMP 灯

LED-RED红色发光二极管

LM016L 2行16 列液晶可显示 2 行16 列英文字符，有8 位数据总线D0-D7 ，RS，R/W，EN三个控制端口（共 14 线），工作电压为 5V。没背光，和常用的 1602B 功能和引脚一样（除了调背光的二个线脚）

LOGICANALYSER 逻辑分析器

LOGICPROBE逻辑探针

LOGICPROBE逻辑探针用来显示连接位置的逻辑状态

LOGICSTATE 逻辑状态用鼠标点击 ,可改变该方框连接位置的逻辑状态

LOGICTOGGLE 逻辑触发

MASTERSWITCH按钮手动闭合 ,立即自动打开

MOTOR 马达

OR 或门

POT-LIN三引线可变电阻器

POWER 电源

RES 电阻

RESISTOR电阻器

SWITCH按钮手动按一下一个状态

SWITCH-SPDT二选通一按钮

VOLTMETER 伏特计

VOLTMETER-MILLImV 伏特计

VTERM 串行口终端

Electromechanical 电机

Inductors变压器

LaplacePrimitives 拉普拉斯变换

Memory Ics Microprocessor Ics

Miscellaneous各种器件 AERIAL-天线；ATAHDD；ATMEGA64；BATTERY；CELL；

CRYSTAL-晶振； FUSE；METER-仪表；

ModellingPrimitives 各种仿真器件是典型的基本元器模拟，不表示具体型号，只用于仿真，没有 PCB

Optoelectronics各种发光器件发光二极管，LED，液晶等等PLDs& FPGAs

Resistors 各种电阻

SimulatorPrimitives 常用的器件

Speakers & Sounders

Switches & Relays开关，继电器，键盘

Switching Devices 晶阊管

Transistors 晶体管（三极管，场效应管）

TTL 74 series TTL 74ALS series

TTL 74AS series TTL 74F series TTL 74HCseries TTL 74HCT series TTL 74LS series TTL 74S series

Analog Ics 模拟电路集成芯片

Capacitors 电容 ** CMOS 4000series

Connectors排座，排插DataConverters ADC,DACDebugging Tools调试工具ECL10000 Series

————————————————————PROTEUS 元件库元件名称及中英对

照

AND 与门

ANTENNA 天线

BATTERY 直流电源

BELL 铃,钟

BVC 同轴电缆接插件BRIDEG1 整流桥(二极管)BRIDEG 2 整流桥(集成块)

BUFFER 缓冲器

BUZZER 蜂鸣器

CAP电容

CAPACITOR 电容

CAPACITORPOL 有极性电容

CAPVAR 可调电容

CIRCUITBREAKER 熔断丝

COAX 同轴电缆

CON 插口

CRYSTAL 晶体整荡器

DB 并行插口

DIODE 二极管

DIODESCHOTTKY 稳压二极管DIODEV ARACTOR变容二极管DPY_3-SEG3 段LED

DPY_7-SEG 7 段LED

DPY_7-SEG_DP7 段 LED(带小数点 )

ELECTRO 电解电容

FUSE熔断器

INDUCTOR 电感

INDUCTORIRON 带铁芯电感

INDUCTOR3 可调电感

JFET N N 沟道场效应管

JFET P P沟道场效应管

LAMP 灯泡

LAMPNEDN 起辉器

LED 发光二极管

METER 仪表

MICROPHONE 麦克风

MOSFETMOS 管

MOTORAC 交流电机

MOTORSERVO 伺服电机

NAND 与非门

NOR 或非门

NOT 非门

NPNNPN 三极管

NPN-PHOTO 感光三极管

OPAMP运放

OR 或门

PHOTO感光二极管

PNP三极管

NPNDAR NPN 三极管

PNPDAR PNP 三极管

POT滑线变阻器

PELAY-DPDT 双刀双掷继电器

RES1.2电阻

RES3.4可变电阻

RESISTORBRIDGE ? 桥式电阻

RESPACK? 电阻

SCR晶闸管

PLUG? 插头

PLUG ACFEMALE 三相交流插头

SOCKET? 插座

SOURCECURRENT 电流源

SOURCEVOLTAGE 电压源

SPEAKER 扬声器

SW? 开关

SW-DPDY ? 双刀双掷开关SW-SPST? 单刀单掷开关SW-PB按钮

THERMISTOR 电热调节器

TRANS1 变压器

TRANS2 可调变压器TRIAC? 三端双向可控硅TRIODE? 三极真空管

VARISTOR 变阻器

ZENER ? 齐纳二极管DPY_7-SEG_DP数码管SW-PB开关

———————————————————————- PROTEUS 原理图元器件库

详细说明

Device.lib 包括电阻、电容、二极管、三极管和 PCB的连接器符号

ACTIVE.LIB 包括虚拟仪器和有源器件

DIODE.LIB 包括二极管和整流桥

DISPLAY.LIB 包括LCD、LED

BIPOLAR.LIB 包括三极管

FET.LIB 包括场效应管

ASIMMDLS.LIB 包括模拟元器件

VALVES.LIB 包括电子管

ANALOG.LIB 包括电源调节器、运放和数据采样 IC

CAPACITORS.LIB 包括电容

CO***IB 包括 4000系列

ECL.LIB 包括ECL10000系列

MICRO.LIB 包括通用微处理器

OPAMP.LIB 包括运算放大器

RESISTORS.LIB 包括电阻

FAIRCHLD.LIB 包括FAIRCHLD 半导体公司的分立器件

LINTEC.LIB 包括 LINTEC 公司的运算放大器

NATDAC.LIB 包括国家半导体公司的数字采样器件

NATOA.LIB 包括国家半导体公司的运算放大器

TECOOR.LIB 包括TECOOR公司的 SCR和TRIAC

TEXOAC.LIB 包括德州仪器公司的运算放大器和比较器

ZETEX.LIB 包括ZETEX 公司的分立器件

遗传算法

Posted on 2025-05-01

知识推理

Posted on 2025-05-01

逻辑的一般原理

基于知识的Agent通过对知识的内部表示进行操作而推理，其核心部件是知识库KB，知识库作为语句的集合，用知识表示语言表达，用以表示关于世界的某些断言，某些语句直接给定，我们尊称其为公理；

Agent如何维护其知识库？

Tell：告诉知识库Agent感知的内容；
Ask：询问知识库应该采取什么行动，这个过程可能包括大量的推理；
Tell:告诉知识库Agent选择的行动后并执行；

如果Agent感知到的可用信息正确，那么Agent得出的结论也一定是正确的，这就是逻辑推理的本质；

语法

命题：具有确切真值的陈述句；
- 原子命题：不能继续分解的命题；
  - 常值命题：不是真就是假的命题；
  - 变量命题：没有具体内容的原子命题；
- 复合命题：可以继续分解的命题，由简单命题用括号和联结词组成；
  - 简单命题是变量命题时，可看作其函数；
联结词：五种常用的联结词如下：
- 否定式:非P，$\neg P$
- 合取式：P且Q，$P\wedge Q$
- 析取式：P或Q，$P\vee Q$
- 蕴含：规则语句，若P则Q,$P\Rightarrow Q$
- 等价：P当且仅当Q，$P \Leftrightarrow Q$
命题公式：我们递归地定义公式WFF
- 命题变元$P$本身就是公式
- $\neg P, P\wedge Q,P\vee Q,P\Rightarrow Q, P \Leftrightarrow Q $都是公式；
- 仅通过有限步使用上述两规则进行命题的联结得到的才是公式
对于含有$n$个命题变元$P_1,P_2,…,P_n$的公式$G$,记为$G(P_1,P_2,…,P_n)$;

语义

模型/解释：可能的模型就是对命题$\alpha$的真值所有可能赋值，用$M(\alpha)$表示；

对公式$G(P_1,P_2,…,P_n)$,指定$(P_1,P_2,…,P_n)$的一组真值，这组真值称为$G$的解释；
语义：每个命题在每个模型内的真值，命题的真值必须通过指定模型确定；
真值表：联结词的运算规则，用如下表来概括
逻辑推理：用蕴含关系推导出结论；
- 可靠性：只导出蕴含句的推理算法称为可靠的；
- 完备的：若推理算法可以生成任意蕴含句；
模型检验：枚举可能的模型检验KB为真时命题$\alpha$为真,即检验$M(KB)\subseteq M(\alpha)$

定理证明

逻辑等价：命题$\alpha,\beta$ 在同样的模型集合中为真，记为$\alpha \equiv \beta$
有效性（永真性）：若命题在任何模型都是真的；
可满足性：若命题在某些模型中为真；
永假性：若命题在任何模型都是假的；

永真蕴含式

化简式 $P \land Q \Rightarrow P$, $P \land Q \Rightarrow Q$
附加式$ P \Rightarrow P \vee Q$, $ Q \Rightarrow P \vee Q$
析取三段论$﹁P, P∨Q ⇒Q$
假言推理 $P, P→Q ⇒Q$
拒取式$ ¬Q, P→Q ⇒¬P$
假言三段论 $P→Q, Q→R ⇒P→R$
二难推理$ P∨Q, P→R, Q→R ⇒R $
全称固化$ (∀x)P(x) ⇒P(y)$
存在固化$ (∃x)P(x) ⇒P(y)$

置换和推理

谓词：带有参数的命题；
- 谓词公式的解释：设D是谓词公式P的非空个体域，若对P中的常量，函数和谓词按如下规定赋值:
  1. 为每个个体常量指派D中的一个元素；
  2. 为每个n元函数指派一个从Dn到D的一个映射，其中
    $$
    Dn = {(x_1, x_2, · · · , x_n)|x_1, x_2, · · · , x_n ∈ D}
    $$
  3. 为每个n元谓词指派一个从$D^n$到{0,1}的映射，则称这些指派为P在D上的一个解释
- 谓词公式的永真性：如果谓词公式P对非空个体域D上的任一解释都取得真值T，则称P在D上是永真的；如果P在任何非空个体域上都是永真的，则称P是永真。
- 谓词公式的可满足性：对于谓词公式P，如果至少存在D上的一个解释，使公式P在此解释下的真值为T，则称公式P在D上是可满足的。
- 谓词公式的永假性：如果谓词公式P对非空个体域D上的任一解释都取真值F，则称P在D上是永假的；如果P在任何非空个体域上均是永假的，则称P永假。
- 谓词公式的等价性：设P与Q是D上的两个谓词公式，若对D上的任意解释，P与Q都有相同的真值，则称P与Q在D上是等价的。如果D是任意非空个体域，则称P与Q是等价的，记作P⇔Q。
在不同谓词公式中，往往会出现谓词名相同但其个体不同的情况，此时推理过程是不能直接进行匹配的，需要先进行置换； W (a) 和W(x)→Q(x)

对谓词W (a)与W (x)谓词名相同，但个体不同，不能直接进行推理。

要使用假言推理，首先需要找到项a对变元x的置换，使W (a)与W (x)一致。这种寻找项对变元的置换，使谓词一致的过程叫做合一的过程。
置换是形如 ${t_1 /x_1 ,t_2 /x_2 ,…,t_n /x_n }$

的有限集合。其中，$t_1 ,t_2 ,…,t_n $是项；$x_1 ,x_2 ,…,x_n $是互不相同的变元；$t_i /x_i$ 表示用$t_i $替换$x_i$ 。要求：$t_i $与$x_i$ 不能相同，$x_i $不能循环地出现在另一个$t_i$ 中。

通常，置换是用希腊字母$θ、σ、α、λ$等来表示的
设$θ={t_1 /x_1 ,t_2 /x_2 ,…,t_n /x_n }$是一个置换，$F$是一个谓词公式，把公式$F$中出现的所有$x_i$ 换成$t_i (i=1,2,…,n)$，得到一个新的公式$G$，称$G$为$F$在置换$θ $下的例示，记作$G=Fθ$

归结(消解)演绎推理背景

归结演绎推理是一种基于鲁宾逊(Robinson)归结原理的机器推理技术。鲁宾逊归结原理亦称消解原理, 鲁宾逊于1965年在海伯伦(Herbrand)理论的基础上提出一种基于逻辑的”反证法”

在人工智能中, 几乎所有的问题都可转化为一个定理证明问题。定理证明的实质, 就是对前提P、结论Q, 证明 P→Q 永真。

要证明P→Q永真, 就要证明P→Q在任何一个非空的个体域上都是永真的。这是非常困难, 甚至是不可实现的。

人们发现可采用反证法的思想, 把关于永真性的证明转化为关于不可满足性的证明。

即要证明P→Q永真, 只要能够证明P∧﹁Q是不可满足的就可。

因：﹁ (P→Q) ⇔ ﹁ (﹁ P∨Q) ⇔ P∧﹁ Q

这方面最有成效的工作就是鲁宾逊归结原理。它使定理证明的机械化成为现实。

爬山算法，模拟退火算法

Posted on 2025-05-01

局部搜索算法

爬山算法

原理

选择随机解作为起点
邻域搜索：在当前解的邻域搜索使目标函数最大化的解
迭代：
- 如果邻居中有性质更好的解，更新为当前解
- 若达到预定迭代次数，或者当前解局部最优停止

Python实现

选取目标函数$f(x)=16-x^2$,函数明显在$x=0$处取得最大值16

优点

简单
目标函数具有单峰性时，效果较好

缺点

局部最优$\neq$全局最优
对初始解和迭代次数敏感

模拟退火算法

最优化问题

Posted on 2025-05-01

最优化问题

最优化问题值得四在一定约束条件下，求一个函数最大(小)值的过程；

由于极大极小问题可以互相转换$\min_x f(x)=-\max_x [-f(x)]$,不失一般性，因此我们统一形式化描述如下：
$$
\begin{aligned}
&\min_{x\in \mathcal X}f(x)\
s.t. \quad &c_i(x)=0,1\le i\le m_e\
&c_i(x)\le 0,m_e+1\le i\le m
\end{aligned}
$$
一般而言，我们的目标是找到全局最小值。但是，有些复杂的目标函数有多个局部最小值点。需要比较这些点处的目标函数值。

梯度下降

驻点的精确求解往往是困难的，在实践中我们往往通过迭代算法找到近似解：从一个初始点$x_0$开始，基于某种规则，从$x_k$移动到下一个点$x_{k+1}$,构造这样一个数列，直到找到使得梯度为0的点为止。
$$
\exists h:\mathbb R\to\mathbb R, x_{k+1}=h(x_k),\lim_{k\to +\infty}\nabla f(x_k)=0
$$
注意Taloy展开如下：
$$
f(x)=f(a)+\frac{f^{\prime}(a)}{1!}(x-a)+\frac{f^{(2)}(a)}{2!}(x-a)^2+\cdots+\frac{f^{(n)}(a)}{n!}(x-a)^n+\frac{f^{(n+1)}(\theta)}{(n+1)!}(x-a)^{(n+1)}
$$
设计$$f(x+\Delta x)-f(x)\approx(\nabla f(x))^\top\Delta x$$

希望做到$f(x+\Delta x)<f(x)$,取$\Delta x=-t\nabla f(x)$可以做到；

其中$t>0$为预先设置的步长，它尽量小；

Steepest Descent

我们希望在第$k$次迭代时，选取合适的步长$t^*$来最优化目标函数$f(x)$;

形式化地说，考虑以下优化问题：
$$
t^*={\arg\min}_{t} f(x_k-t\cdot \nabla f(x_k))
$$
但是这仍然面临着一元函数求驻点的问题；

Stochastic Gradient Decent，SGD

随机梯度下降法考虑对每个样本都进行更新：
$$
\theta_{t+1}=\theta_{t}-\alpha\frac{\partial\mathcal{L}\big(\theta_{t};x^{(t)},y^{(t)}\big)}{\partial\theta}
$$
其中步长$\alpha$也被称为学习率（Learning Rate）,损失函数和学习率的关系如下：

随机梯度下降的伪代码如下：

Mini-batch SGD

小批量随机梯度下降法
$$
\begin{aligned}\theta_{t+1}&=\theta_{t}-\alpha\frac{\partial\mathcal{R}(\theta)}{\partial\theta_{t}}\&=\theta_t-\alpha\frac1N\sum_{i=1}^N\frac{\partial\mathcal{L}\big(\theta_t;x^{(i)},y^{(i)}\big)}{\partial\theta}\end{aligned}
$$

Stopping Criteria

使用一个验证集（Validation Dataset）来测试每一次迭代的参数在验证集上是否最优。如果在验证集上的错误率不再下降，就停止迭代；

这是为了避免算法陷入了局部最优或者鞍点，但我们要找的是全局最小值；

凸优化

凸集：对于$n$维空间中点的集合$C$，若对集合中的任意两点$x$和$y$，以及$0≤θ≤1$，都有$θx+(1-θ)y∈C$，则称该集合为凸集;

凸函数的判定：

对于$n$维空间中点的集合$C$，如果对集合中的任意两点$x$和$y$，以及实数$0≤θ≤1$，都有$f(θx+(1-θ)y)≤θf(x)+(1-θ)f(y)$;
Hessian矩阵为半正定矩阵
$$
\mathbf{H}=\begin{bmatrix}\dfrac{\partial^2f}{\partial x_1^2}&\dfrac{\partial^2f}{\partial x_1\partial x_2}&\cdots&\dfrac{\partial^2f}{\partial x_1:\partial x_n}\\\dfrac{\partial^2f}{\partial x_2:\partial x_1}&\dfrac{\partial^2f}{\partial x_2^2}&\cdots&\dfrac{\partial^2f}{\partial x_2:\partial x_n}\\\vdots&\vdots&\ddots&\vdots\\\dfrac{\partial^2f}{\partial x_n:\partial x_1}&\dfrac{\partial^2f}{\partial x_n:\partial x_2}&\cdots&\dfrac{\partial^2f}{\partial x_n^2}\end{bmatrix}
$$

简单来说，凸优化问题就是同时满足凸函数+凸集的最优化问题，全局最优解的寻找直接被简化成局部最优解；

常见的约束条件有：

线性约束：$ {x∈R^n:Ax=b}$
多面体约束：$ {x∈R^n:Ax≤b}$

注意到，多个凸集的交集还是凸集，因此，优化问题中可能有多个等式和不等式约束，只要每个约束条件定义的可行域是凸集，则同时满足这些约束条件的可行域还是凸集；

严谨地说，如果一个最优化问题的可行域是凸集，并且目标函数是凸函数，则该问题为凸优化问题；

形式化描述如下：
$$
\min f(x), \
s.t. h_i(x)=0,i=1,…,k\
g_i(x)\leq0,i=1,…,l\
其中仿射函数h_i(x)为等式约束，\
凸函数g_i(x)为不等式约束
$$
目前，不少问题都是凸优化问题，比如线性回归，岭回归，支持向量机，Logistic回归；

损失函数

Uninformed Search

Posted on 2025-05-01

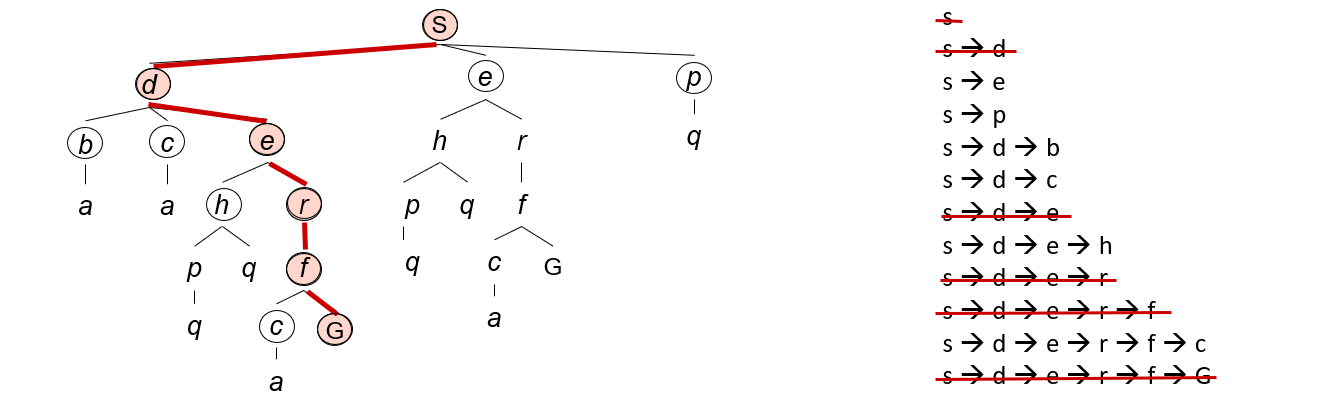
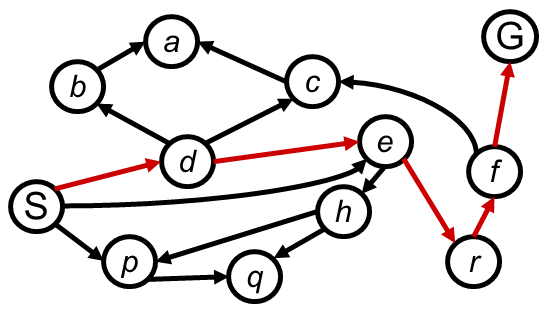
假设下面搜索问题按照下图举例：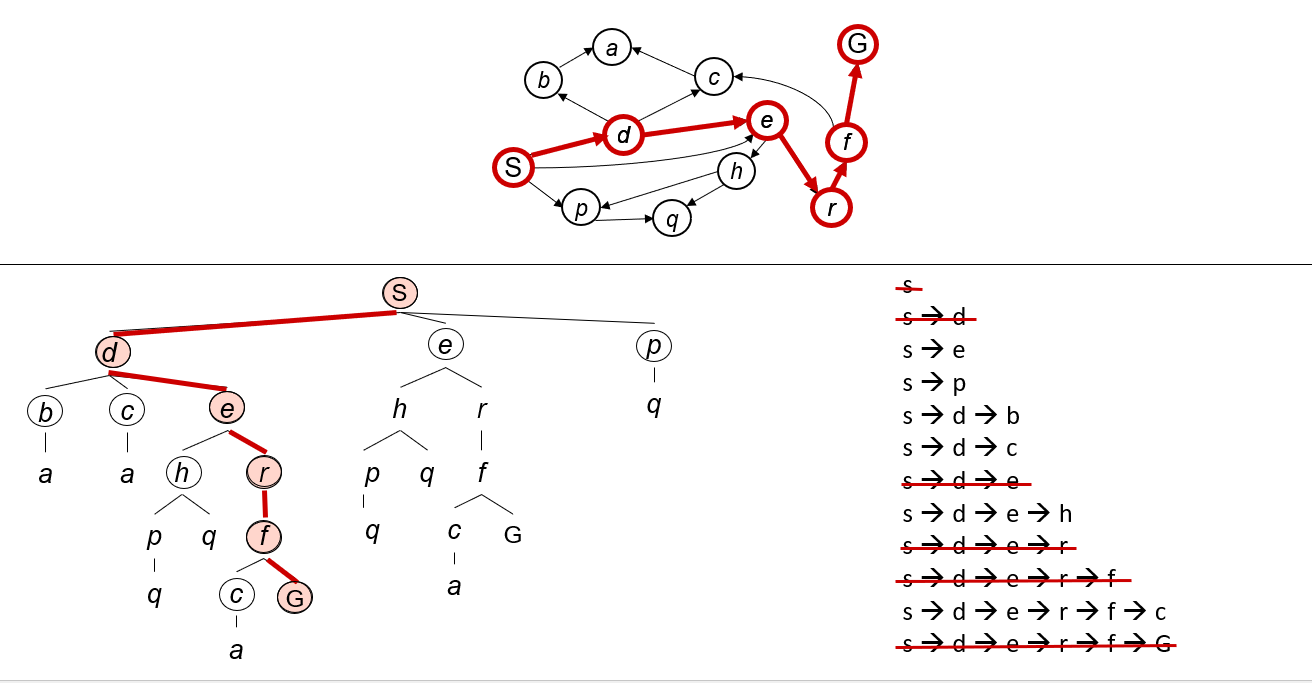

Depth-first Search

DFS总是拓展搜索树中当前边缘节点集中的最深的结点，很快搜索推进到没有后继的最深层，将它们从边缘节点集去掉后，回溯到下一个稍浅的未拓展后继的结点；

做到这一点的关键是维护一个栈，每次保证当前看到最深的结点在栈顶，优先弹出的也是已经被搜完的栈顶结点；

我们从四个性能度量考察DFS：

完备性：
- 在避免了重复状态和冗余路径，优先状态空间中图搜索完备；
- 但是对于树搜索可能会陷入死循环，不过可以优化检查根节点到当前结点的新节点，但还是无法避免冗余路径；
- 遭遇无限且无法到达目标结点的路径则会失败；
最优性：优先左子树可能会导致路径变长，代价变大，错过最优解，尽管到达了目标结点；
时间复杂度：若搜索一致树每个状态有$b$个后继，对于$m$为任意结点的最大深度，$d$为最浅解的深度，DFS可能会在搜索树上生成所有$O(b+b^2+\cdots+b^m)=O(b^m)$个结点；
空间复杂度：只需要存储根节点到叶节点的路径可以做到$O(bm)$，具有很大优势；

Breadth-first Search

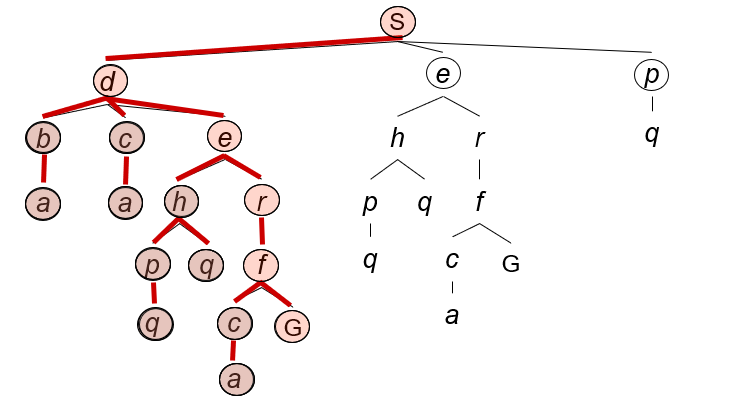
BFS总是拓展深度最浅的结点，直到目标检测被通过。这意味着浅层的结点会在深层结点来临之前被拓展，这通过队列(Queue)很容易实现；

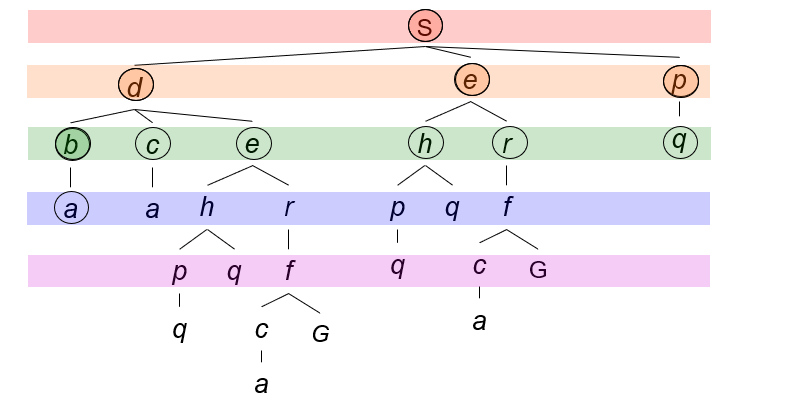
我们从四个方面考察BFS的性能：

完备性：若通过结点通过目标检测，那么一定是最浅结点，因为更浅的结点没有通过目标检测；因此BFS是完备的；
最优性：若路径代价是基于深度的非减函数，那么BFS是最优的；
时间复杂度：最坏情况下目标为最后一层结点，解的深度为$d$,目标检测在选择拓展结点时，时间复杂度为$O(b^{d+1})$;
空间复杂度：已拓展的每个结点都保存在探索集中，因此空间复杂度为$O(b^d)$,几乎不能忍受；

Uniform-cost Search

UCS总是拓展代价最小的结点，直到需要将边缘结点集组织成按代价排序的优先队列来实现；

下面从四个方面考察UCS的性能：

完备性：UCS对解路径的步数并不关心，因此若存在零代价的行动，那么UCS可能会陷入死循环，否则代价都是正直的话，UCS是完备的；
最优性：目标检测发生于结点被拓展时进行，而不是在生成时进行，第一个生成的目标结点可能在次优路径上，也就是说目标结点被搜索到时并不会立即停止算法，而是等待可能到目标结点的路径都被（部分，因为代价过大的路径可能就不会搜了）探索过后，比较最小的代价后再返回；
时间复杂度：假设最优解代价为$c$,单步行动最小代价为$\varepsilon$,那么最坏时间复杂度为$O(b^{1+[\frac c\varepsilon]})$,因为在探索代价大的行动前，会先探索代价小的行动所在的搜索树；
空间复杂度：同$O(b^{1+[\frac c\varepsilon]})$

Depth-limited Search

为了避免无限循环的DFS失败，对DFS设置探索界限$l$，深度为$l$的结点被视作没有后继；

选择一个好的$l$值往往是困难的，对于大多数问题，如果它没被解决，是无法知道一个好的深度界限的；

我们从四个方面考察DLS的性能：

完备性：设置$l<d$,DLS无法搜到目标节点，也就是不完备的；
最优性：设置$l>d$,同DFS一样不是最优的；
时间复杂度：被剪枝为$O(b^l)$;
空间复杂度：$O(bl)$;

Iterative Deepening Search

结合DFS和BFS的优势，它经常和深度优先搜索结合使用确定更好的深度界限；

初始化深度限制$l=0$,不断增大它，直到找到目标，当$l=d$的时候，即最浅的目标节点所在深度时，就能找到；

我们从四个方面考察IDS的性能：

完备性：同BFS，分支因子有限时搜索算法完备；
最优性：同BFS，代价函数为结点深度的非减函数时最优；
时间复杂度：上层结点被重复生成，存在解时时间复杂度为$O(db+(d-1)b^2+\cdots+b^d)=O(b^d)$;
空间复杂度：同$O(bd)$;

Bidirectional Search

并不是每一个问题都能运用双向搜索，比如8皇后问题，但是对于一个使用BFS的搜索问题，解的深度为$d$意味着时间复杂度为$O(b^d)$,但是同时对起始和目标同时BFS直到相遇看起来时间复杂度为$O(2b^{d/2})$,这要小得多；

Search and Models

Search operates over models of the world

The agent doesn’t actually try all the plans out in the real world;
Planning is all “in simulation”
Your search is only as good as your models…

Search Problems

Posted on 2025-05-01

Search-Problem的形式化描述

对于一个planning-agent，设立一个目标goal以满足其最大化性能，如果Agent达到了goal，我们的Search-Problem也就得到了解决；

第一步就是要形式化地描述这个Agent的性能度量，一般地，对于一个Search-Problem来说，有几个要素：

a state space：状态空间
a successor function：转移模型{action, costs}描述状态a通过某个行动转移到状态b以及可能的代价的函数；
a initial state：初始状态
a goal test

如果我们称一个Search-Problem找到了solution，也就是找到了一个行动序列，或者说一个plan，从初始状态移动到目标状态，这样的找到solution的过程称为搜索；

所有的Search-Problm都是模型Model；

Romania Map Example

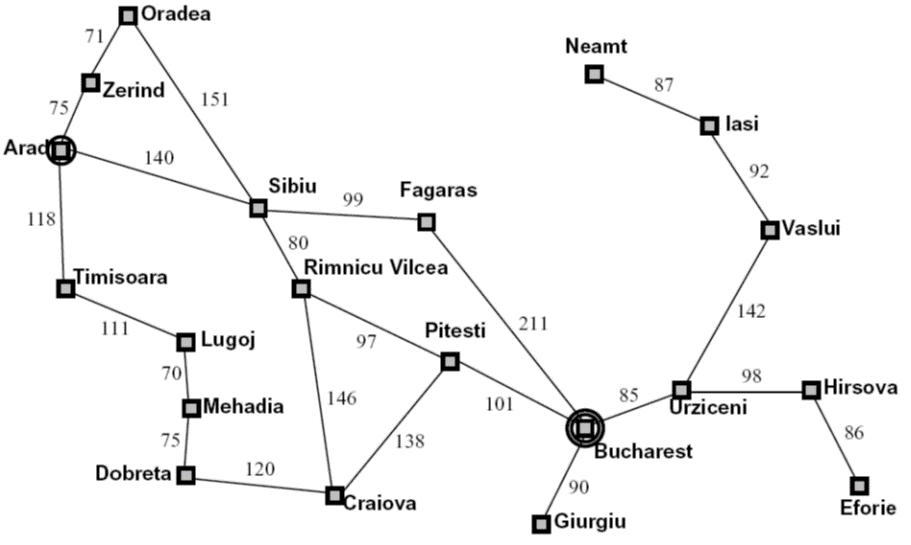
对于Agent在Romania的Arad旅游，可以如下地形式化描述：

State space:Cities
Successor function:
- Roads: Go to adjacent city
- cost：distance
Start state:Arad
Goal test: Is state == Bucharest?
Solution?

Search Space Graphs&Search Trees

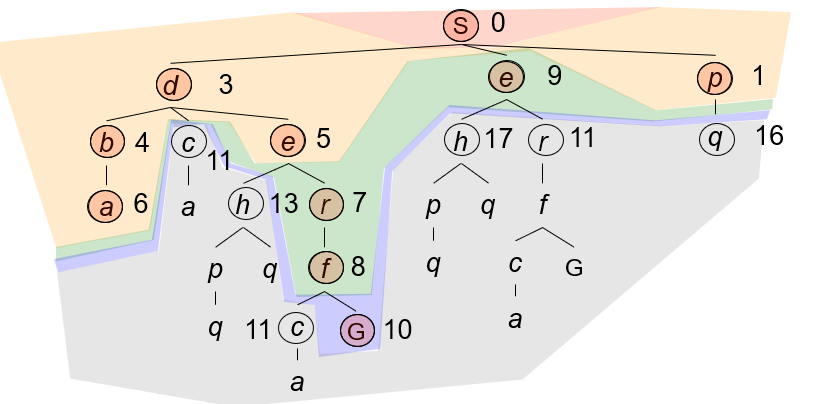
一个搜索算法需要考虑各种可能的行动序列，而状态图就是搜索问题的数学描述，每个状态在状态图仅出现一次形成结点，而搜索过程往往是沿着图中的一棵树上进行的；

根节点从初始状态出发；
结点表示状态空间的状态；
连线表示行动，一次合法的行动将会拓展当前状态，生成一个新的状态集，也就是从父节点出发得到如若干子节点；
给定某个搜索时刻。还没展开的叶节点称为边缘;
选择展开的结点的顺序就是搜索策略；

我们往往很难在内存中将状态图存储，甚至对大多数问题，我们也没必要真的建立整棵搜索树；

下面是一个例子来描述状态图和搜索树的；

在搜索过程中，有些冗余状态和冗余路径是不可避免的，但是可能状态是有限的，因此那些遗忘搜索历史的算法可能会不幸地重复历史；

引入探索集(closed表，fringe)，记录每个已拓展地结点,常用Hash表实现，加入Hash表的数据结构一定要是可哈希的，比如对于numpy.ndarray,可以用tobites()方法转化成字节序列，这是一个可哈希的数据结构；

在搜索算法中我们要选择下一个拓展的结点，比较合适的数据结构是队列，包括FIFO队列（Queue），LIFO队列（Stack），优先队列（priority_queue）;

General Tree Search

对于通用搜索树来说，有三点需要注意：

Fringe
Expansion
Exploration strategy

关注解决哪个结点是需要拓展的问题，算法的性能有一个考量：

完备性：是否能找到解？
最优性：是否能找到最优解（最小代价）？
时间复杂度；
空间复杂度；

对于上述例子的搜索过程，我们可以这样表示它的过程；

Random Games

Posted on 2025-05-01

FileTree

Usage

基于Multisim的方波-三角波-正弦波-锯齿波函数发生器电子电路仿真项目设计

摘要

目录

第一章：前言、课程设计任务与要求

第二章：电路设计原理

2.1 正弦波产生电路工作原理

2.2 方波产生电路工作原理

2.3 三角波产生电路工作原理

2.4 锯齿波产生电路工作原理

第三章：Multisim仿真项目实验数据与方法记录

3.1 正弦波发生实验数据与方法

3.2 方波发生实验数据与方法

3.3 三角波发生实验数据与方法

3.4 锯齿波发生实验数据与方法

第四章： 总结与体会

第一章：前言、课程设计任务与要求

第二章：电路设计原理

2.1 正弦波产生电路工作原理

2.1.1 产生正弦振荡的条件：

2.1.2 基本组成部分及其作用

2.1.3 文氏桥正弦型振荡电路及分析

2.2 方波产生电路工作原理

2.2.1 产生方波的条件

2.2.2 基本组成部分及作用

2.2.3 滞回比较器电路及分析

2.3 三角波产生电路工作原理

2.3.1 基本组成部分及作用

2.3.2 串联分析

2.4 锯齿波产生电路工作原理

2.4.1 基本组成部分及作用

2.4.2 基本组成电路

第三章：Multisim仿真项目实验数据与方法记录

3.1 正弦波发生实验数据和方法

3.2 方波发生实验数据与方法

3.3 三角波发生实验数据与方法

3.4 锯齿波发生实验数据与方法

第四章：总结与体会

逻辑的一般原理

语法

语义

定理证明

永真蕴含式

置换和推理

归结(消解)演绎推理背景

局部搜索算法

爬山算法

原理

Python实现

优点

缺点

模拟退火算法

最优化问题

梯度下降

Steepest Descent

Stochastic Gradient Decent，SGD

Mini-batch SGD

Stopping Criteria

凸优化

损失函数

Depth-first Search

Breadth-first Search

Uniform-cost Search

Depth-limited Search

Iterative Deepening Search

Bidirectional Search

Search and Models

Search-Problem的形式化描述

Romania Map Example

Search Space Graphs&Search Trees

General Tree Search

第四章：总结与体会