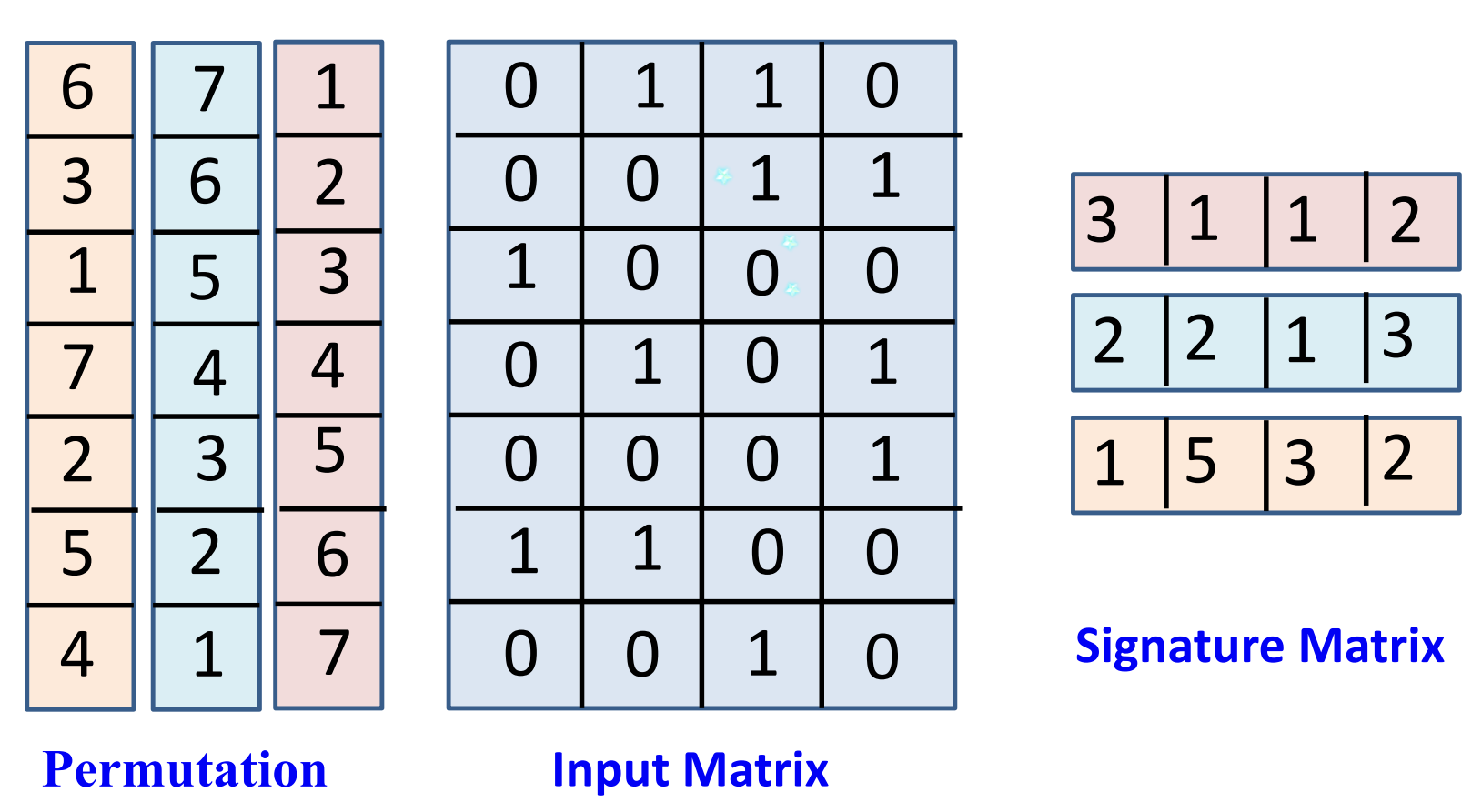
数据流挖掘
Background
Content
数据流的三个特征
- One by one
- Potentially Unbounded
- Concept Drift
数据流挖掘的四个挑战
- 单程处理Single Pass Handling
- 内存限制Memory Limitation
- 时间复杂度Low Time Complexity
- 概念漂移 Concept Drift
什么是概念漂移
In predictive analytics and machine learning, the concept drift means that the statistical properties of the target variable, which the model is trying to predict, change over time in unforeseen ways.
在预测分析和机器学习中,概念漂移意味着模型试图预测的目标变量的统计属性会随着时间而以不可预见的方式发生变化;
模型的概率分布发生变化,表现三个方面:$P(C),P(X),P(C|X)$
这些变化可能是重要的,例如,对较旧的历史数据进行训练的模型所做的预测不再正确或者如果模型是根据最近的历史数据进行训练那么正确。
反过来,可以检测这些变化,并且如果检测到,则可以更新学习的模型以反映这些变化。
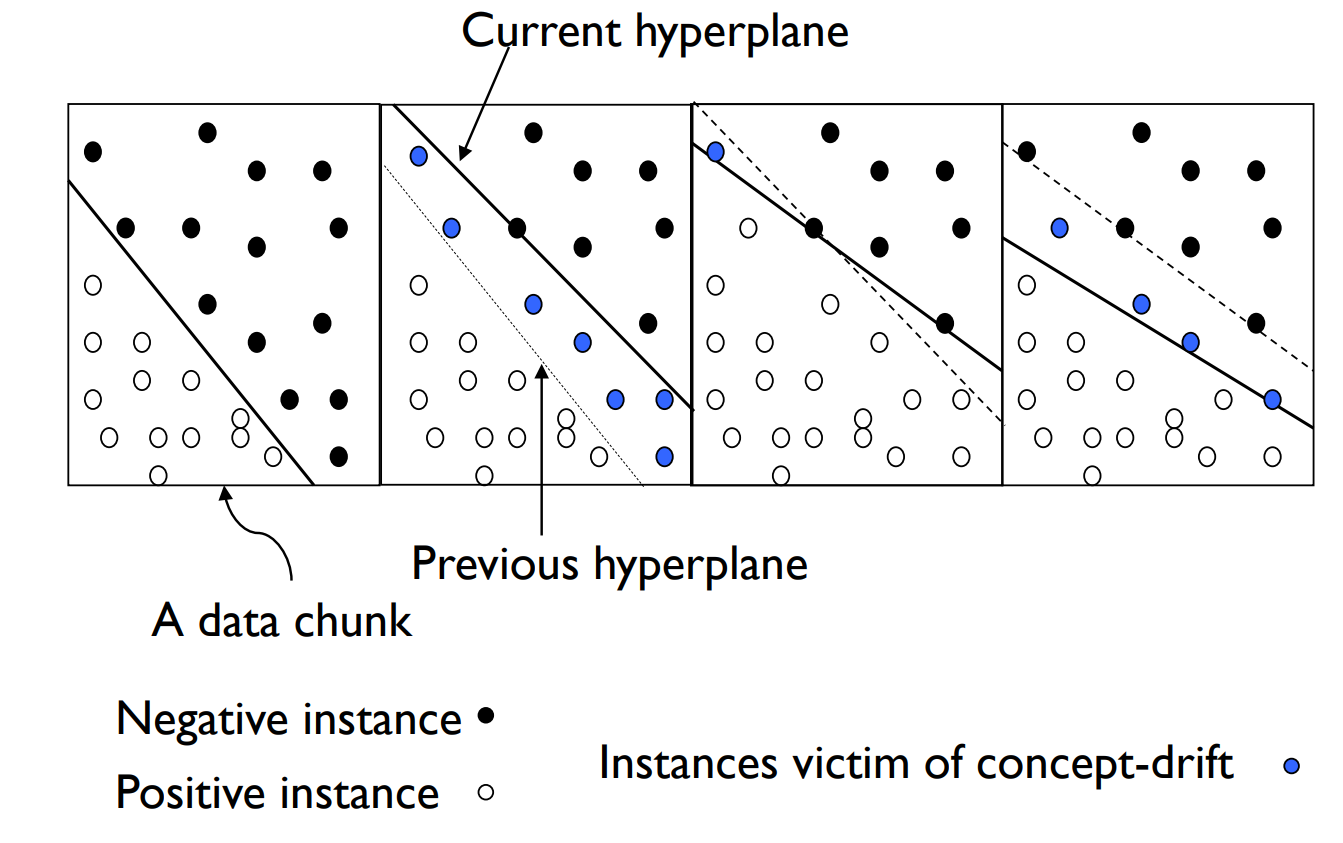
Real concept drift vs. Virtual concept drift

真实概念漂移指的是数据的分布和目标概念(即预测的目标变量的条件分布)同时发生变化。也就是说,输入特征与输出变量之间的关系发生了变化。这种漂移对机器学习模型的影响更为显著,因为模型的预测准确性可能会显著下降。真实概念漂移通常发生在以下情况中:
- 市场变化:消费者的偏好和行为模式随着时间的推移而变化。例如,一个预测消费者购买行为的模型在几年后可能变得不准确,因为消费者的偏好和市场趋势发生了变化。
- 环境变化:自然环境的变化可能影响预测模型的准确性。例如,气候变化可能影响农业产量预测模型的准确性,因为气候条件与作物产量之间的关系发生了变化。
- 社会变化:社会和政策变化也会导致真实概念漂移。例如,新的法规可能改变企业运营的方式,从而影响金融风险预测模型的准确性。
虚拟概念漂移(Virtual Concept Drift):
虚拟概念漂移指的是数据的分布发生变化,但目标概念(即预测的目标变量的条件分布)没有变化。这种漂移主要影响输入特征的分布,而不改变输入特征与输出变量之间的关系。虚拟概念漂移的主要特征是,虽然输入特征的统计特性改变了,但这些变化不会导致模型预测目标的条件概率发生变化。因此,模型的准确性可能不会受到显著影响,但如果模型包含假设输入特征的分布是静态的,那么它可能需要更新以更好地适应新的输入分布。例如:
- 在天气预报中,如果温度的分布在不同季节中变化,但温度与预测的天气(如晴天、雨天等)之间的关系保持不变,则属于虚拟概念漂移。
- 在一个电子商务平台上,用户的浏览行为模式可能随时间变化(例如假期期间),但这些行为与购买意图之间的关系未变。
概念漂移的检测
ADWIN算法(Adaptive Windowing):基于分布的办法
Monitoring the change of data distributions between two fixed or adaptive windows of data.
监视两个固定或自适应数据窗口之间的数据分布变化。
The idea is simple: whenever two “large enough” subwindows of W exhibit “distinct enough” averages, one can conclude that the corresponding expected values are different,and the older portion of the window is dropped
这个想法很简单:每当 W 的两个“足够大”的子窗口表现出“足够明显”的平均值时,就可以得出结论,相应的期望值是不同的,并且窗口的较旧部分被丢弃
可能的三个挑战:
- Hard to determine window size;难以确定窗口大小
- Learn concept drift slower;学习概念漂移的速度较慢
- Virtual concept drift;虚拟概念漂移

PHT 基于错误率的办法
Capture concept drift based on the change of the classification performance. (i.e. comparing the current classification performance to the average historical error rate with statistical analysis.) (e.g. PHT)
根据分类性能的变化捕获概念漂移。(即通过统计分析将当前分类性能与平均历史错误率进行比较。(例如:PHT)
- Sensitive to noise 对噪音敏感
- Hard to deal with gradual concept drift 难以应对渐进式概念漂移
- Depend on learning model itself heavily 严重依赖学习模型本身
漂移检测方法:DDM
The theory guarantees that while the class distribution of the examples is stationary , the error rate of the learning algorithm will decrease when i increases. A significant increase in the error of the algorithm, suggest a change in the class distribution, and whether is a significant increase is based on following formula.
该理论保证了当样本的类分布是平稳的时,学习算法的错误率会随着i的增加而降低。算法误差的显著增加,表明类分布发生了变化,是否显著增加取决于以下公式;
$$
p_i+s_i\ge p_{min}+3s_{min}
$$
数据流分类
- Process an example at a time, and inspect it only once
- Be ready to predict at any point
- Use a limited amount of memory
- Work in a limited amount of time
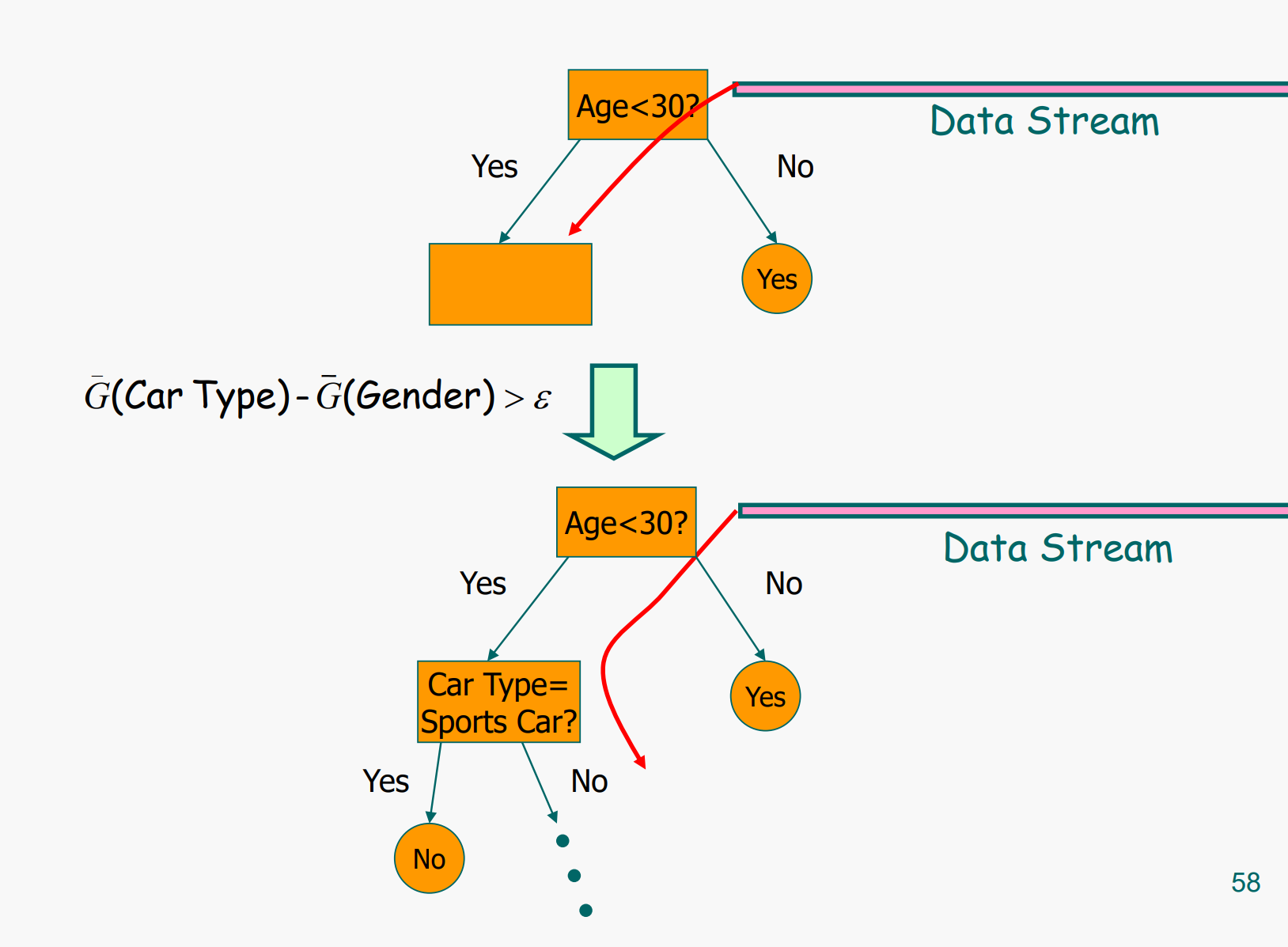
VFDT (Very Fast Decision Tree)
A decision-tree learning system based on the Hoeffding tree algorithm
基于Hoeffding树算法的决策树学习系统
In order to find the best attribute at a node, it may be sufficient to consider only a small subset of the training examples that pass through that node.
为了在节点上找到最佳属性,只需考虑通过该节点的训练示例的一小部分就足够了。
Given a stream of examples, use the first ones to choose the root attribute.
给定一系列示例,使用第一个示例来选择 root 属性
Once the root attribute is chosen, the successive examples are passed down to the corresponding leaves, and used to choose the attribute there, and so on recursively.
一旦选择了根属性,连续的例子就会传递到相应的叶子上,并用于选择那里的属性,依此类推递归。
Use Hoeffding bound to decide how many examples are enough at each node
使用 Hoeffding bound 来决定每个节点上有多少个示例就足够了
数据流聚类
微簇Micro-Clusters
A Micro-Cluster is a set of individual data points that are close to each other and will be treated as a single unit in further offline Macro-clustering
微簇是一组彼此接近的单个数据点,在进一步的离线宏集群中将被视为单个单元
Online micro-cluster maintenance在线微集群维护
Initial creation of q micro-clusters q 微簇的初始创建
q is usually significantly larger than the number of natural clusters q通常明显大于自然簇的数量
Online incremental update of micro-clusters 微集群在线增量更新
If new point is within max-boundary, insert into the micro cluster
o.w., create a new cluster May delete obsolete micro-cluster or merge two closest ones
Offline Phase: Query-based macro-clustering
Based on a user-specified time-horizon h and the number of macro-clusters k, compute macroclusters using the k-means algorithm
Cluster Feature: CF = (N, LS, SS)
- (N) - 数量:
- (N) 是簇中数据点的总数。这提供了簇的规模信息。
- (LS) - 线性和:
- (LS) 是簇中所有数据点向量的逐元素和。对于d维数据点,如果簇中有k个数据点,则
$$LS = \sum_{i=1}^{k} \mathbf{x}_i$$
其中$ (\mathbf{x}_i)$ 是第 (i) 个数据点向量。这一项用于计算簇的质心(中心点)。
- (SS) - 平方和:
- (SS) 是簇中所有数据点向量的逐元素平方和。即
$$SS = \sum_{i=1}^{k} \mathbf{x}_i^2$$
其中 $(\mathbf{x}_i^2) $表示第 (i) 个数据点向量的逐元素平方和。这一项用于计算簇的散布(方差或标准差)。
Hadoop/Spark
设计准则:大规模数据处理,并行化,容错率及恢复,简明接口
Hadoop
Hadoop是一个开源的分布式计算框架,用于处理和存储大规模数据集。它由Apache软件基金会开发和维护,提供了高可靠性、可扩展性和分布式处理能力。Hadoop的核心组件包括:
HDFS(Hadoop Distributed File System):
- HDFS是一个分布式文件系统,负责存储大规模数据。它将数据分成块(通常64MB或128MB),并在集群中的多个节点上进行复制存储,以提高数据的可靠性和可用性。
MapReduce:
- MapReduce是Hadoop的分布式计算模型。它将计算任务分为两个阶段:Map阶段和Reduce阶段。Map阶段处理输入数据并生成中间结果,Reduce阶段合并中间结果以生成最终输出。
YARN(Yet Another Resource Negotiator):
- YARN是Hadoop的资源管理系统,负责管理和调度集群资源,协调不同应用程序的执行。
Hadoop生态系统:
- Hadoop有一个庞大的生态系统,包括Pig(数据流脚本语言)、Hive(数据仓库基础设施)、HBase(分布式数据库)、Sqoop(数据导入导出工具)、Flume(日志数据收集工具)等。
Spark
Spark是一个开源的分布式计算系统,旨在提高数据处理速度和效率。由UC Berkeley的AMP实验室开发,后来成为Apache软件基金会的顶级项目。Spark提供了一个统一的分析引擎,可以处理批处理、流处理、交互式查询和机器学习任务。其核心组件包括:
RDD(Resilient Distributed Dataset):
- RDD是Spark的核心抽象,表示一个分布式的、不可变的数据集合。RDD支持两种操作:转换(如map、filter)和动作(如count、collect)。RDD的弹性体现在其自动容错和重计算能力上。
Spark SQL:
- Spark SQL提供了对结构化数据的支持,允许使用SQL查询和数据框(DataFrame)API来处理数据。它集成了Hive元数据,可以直接查询Hive表。
Spark Streaming:
- Spark Streaming支持实时数据流处理。它将实时数据流分成小批次,并使用Spark引擎进行处理,适用于日志分析、实时监控等场景。
MLlib(机器学习库):
- MLlib是Spark的机器学习库,提供了多种机器学习算法,如分类、回归、聚类和协同过滤等,以及特征提取和评估工具。
GraphX:
- GraphX是Spark的图计算库,支持图结构的并行计算和图算法,如PageRank、Connected Components等。
Spark生态系统:
- Spark的生态系统包括各种与数据处理相关的工具和库,如Delta Lake(数据湖管理)、Koalas(Pandas与Spark DataFrame的统一API)、MLflow(机器学习生命周期管理)等。
比较
处理模式:
- Hadoop主要适用于批处理,数据处理延迟较高。
- Spark不仅支持批处理,还支持实时流处理和交互式查询,处理速度更快。
编程模型:
- Hadoop的MapReduce模型较为复杂,需要显式地编写Map和Reduce函数。
- Spark提供了更高层次的API,如DataFrame和Dataset,使编程更加简洁和易用。
性能:
- Hadoop的MapReduce在处理大量小文件时性能较差。
- Spark在内存中进行计算,性能显著提升,尤其在迭代计算和交互式查询中表现更佳。
生态系统:
- Hadoop有一个成熟的生态系统,支持广泛的数据存储和处理工具。
- Spark的生态系统不断扩展,提供了强大的实时处理和高级分析功能。
适用场景
- Hadoop:适用于批处理、大规模数据存储和离线分析任务,如日志分析、数据仓库构建等。
- Spark:适用于实时数据处理、机器学习、图计算和交互式数据分析,如实时流处理、推荐系统、数据科学等。
总之,Hadoop和Spark各有优劣,适用于不同类型的数据处理需求。根据具体的业务需求和数据特性选择合适的框架可以最大化数据处理效率和效果。