树&森林

若一个连通图没有圈，称这个图为树(Tree);

若一个图没有圈，称这个图为森林(forest);

Theorem

若树至少有个点，那么至少包含2个叶子结点；

proof:取最长路的两个端点；

Theorem

对于含有个结点的简单图，以下命题等价：

  1. 是一棵树；
  2. 有条边且没有圈；
  3. 有条边且连通；
  4. 连通，且每条边都是桥；
  5. 中任意两个点有且仅有一条路径；
  6. 没有圈，但是任意添加一条边恰好形成一个圈；

proof:

:归纳，删去叶子

:归纳，每个连通分量无圈，说明分量是树，统计边发现只有一个连通 分量；

:只需证个点的连通图至少有条边，归纳，删叶子即可；

:由连通性至少有一条，若存在两条，则这两条路径上的边不是桥，矛盾；

:若有圈则任意两点至少两条路径，矛盾；加一条边至少形成一个圈，若多余1个，说明原图有圈，矛盾；

:反证，若不连通，每个分量是树，在分量之间添加一条边无法形成圈，矛盾；

Corollary

若图是一个森林,则

Spanning Tree

图的生成子树(spanning tree)是指图的一个生成子图，这个子图是树；

对于连通图,一定包含一个生成子树；定义陪树(cotree)为中去除得到的图；

对于一个具有个顶点，条边，个连通分量的图,通过删除图中任意一条边，直到没有圈剩下，得到的图是图的一个生成森林；

  • 圈阶:在这个过程删除的边数
  • 键阶:最小边割的边数;

对与连通图和其生成子树，

定义子树的键基本集(bond fundamental set)：删去子树将图划分为两个顶点集，连接的所有边构成图的键，通过这种方式获得的键的全体构成基本集；

类似定义子树的圈基本集(cycle fundamental set)

Theorem

对于图的任意生成子树,有

  • 图的任意键和至少有一条公共边；
  • 图的任意圈和的陪树至少有一条公共边；

proof:取是图的键，删去将图分成两部分，一定有边连接这两部分，这条边一定属于键；若圈和陪树没有公共边，那么圈一定包含在中，矛盾；

Prufer序列

给定由个数构成的集合，记是定义在上的一棵树；

定义的Prufer编码,是长度为的序列，显然；

编码算法如下：

  1. 维护的叶子集合;
  2. 在第步，找到中标号最小的叶子, 令是叶子的父亲；
  3. 更新；若因为删去成为叶子，
  4. 直到只剩下一条边，停止；

解码算法如下：

  1. 维护未加标记点集和未使用的编码点集,初始化，初始化图为个孤立点
  2. 准备第步，取出,此时,中至少有2个点不会出现在中，即;
  3. 取为中标号最小的顶点，添加到，标记，(即从位开始，指针右移)；
  4. 重复2，3一共次，剩下两个未标记的顶点，连边并加入;

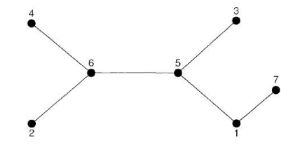
举例：以下树的Prufer编码为[6,5,6,5,1],发现编码删边的顺序和解码加边的顺序相同；

image-20241110170746044

Theorem(Caylay)

对于个顶点，一共有个不同的标号树；

proof:只需要证明树作Prufer编码和解码，依然得到树,完成双射，归纳即可（删去第一个叶子后采用归纳假设）；

Corollary

有个生成子树；

矩阵树

定义连通图，定义其生成子树的数量为;记其Laplacian矩阵为；

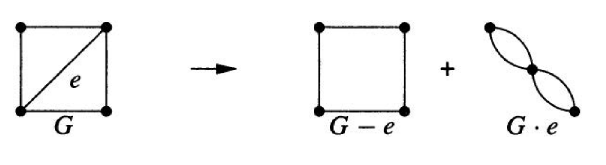
对于图和其中一条边，定义其缩边为合并的两个顶点为一个顶点，原来和两个顶点关联的边都和新顶点相关联；

Theorem

若且不是自环，则

为此只需证明的生成树和中包含的生成树之间可建立双射即可；

image-20241110173825906

Theorem

假设是从中删除行列得到的矩阵，则生成树的数目等于的任何余子式的值；

proof:为此只需证明的情况

树中的最优化问题

The Connector Problem

将建立连接多个城镇的铁路网。考虑到在城镇和之间建造直接连接的成本，设计这样的网络以最大限度地降低建设总成本;

这个问题可进一步形式化描述如下：

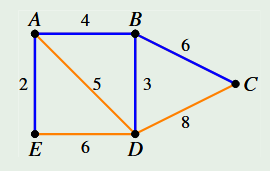
给定一个连通加权图，如果的边权之和不超过的任何其他生成树之和，则生成树称为最小权重生成树,现需要找到图的最小生成子树权和；

Kruskal算法

Kruskal算法用于解决一类稀疏带权图的最小生成树问题,这是一类基于添加当前最优边的贪心策略；

  1. 初始化，,对边权值排序；
  2. 若下一条权值最小的边将的两个分量连接起来，则，否则丢弃它；
  3. 迭代总共步加边操作，此时变得连通；

image-20241110174953351

Kruskal算法最优性证明：

假设Kruskal生成树，其一定不包含圈，否则一定存在某次加边操作，没有连接两个分量而是在某一个分量内部连接；

假设最小代价树，边排序后，考虑它们不相同的第一条边;将产生圈，取,那么是比更小代价的生成树，矛盾；

数据结构实现：

顺序迭代边可采用优先队列（堆）；

为每个顶点记录包含的连通分量标号，初始为其序号；

对于选用某条边时，应该有，否则被弃用；

添加边后，应该更新;

时间复杂度应为;

或是维护边的并查集

Prim算法

Prim算法用于一类稠密带权图的最小生成树问题，这时一类逐步归并顶点的策略；

  1. 任意选择树的根节点，初始化已包含顶点集,树;
  2. 选择连接和中的边权值最小者,更新;
  3. 重复添加顶点，直到;

Prim算法最优性证明：

假设Prim生成树，其一定不包含圈，因为每次加边操作都是在不相交的集合中选择的；

假设最小代价树，边排序后，考虑它们不相同的第一条边;取,由的最小性，，由算法最小性;

数据结构实现：

存取图使用邻接表,采用斐波那契堆优化，可达到;