Poisson过程

计数过程

随机过程 称为计数过程，如果表示从时刻0到某一特定事件发生的次数，它具备以下两个特点：

  1. 且取值为整数；
  2. 时， 且 表示时间内事件发生的次数。

Poisson过程

计数过程称为参数为的Poisson过程，如果

  2. 过程有独立增量；

  3. 对 任 意 的 ,

等价定义如下：

  2. 过程有平稳独立增量；

  3. 存在,当时

  4. 当0时，

计算机如何模拟Poisson过程？下面是一个基于样本路径的性质的又一等价定义：

  1. 每次时间发生的间隔相互独立；
  2. 服从参数为​的指数分布；

这告诉只需要产生足够多的同指数分布的随机数，依次相加得到时间发生的时刻，分段就得到了Poisson过程的一条样本路径.

Mark

  • 参数​​​被称作Poisson过程的速率(强度)；

  • 常见模型有：普通的排队系统，简单的保险公司索赔

  • 第一定义推导第二定义显然，下面是一种由第二定义推导第一定义的办法：

    对于任意给定的,构造.有以下断言：

    1. 几乎就是:

    2. 越来越像Poisson分布：

    独立同分布那么由于因此

    \lim_{n\to \infty}P(X_n=k)=\frac{(\lambda t)^k}{k!}e^{-\lambda t}

Poisson过程的样本路径

,表示第次事件发生的时刻，规定 ,表示第次与第​次事件发生的时间间隔.

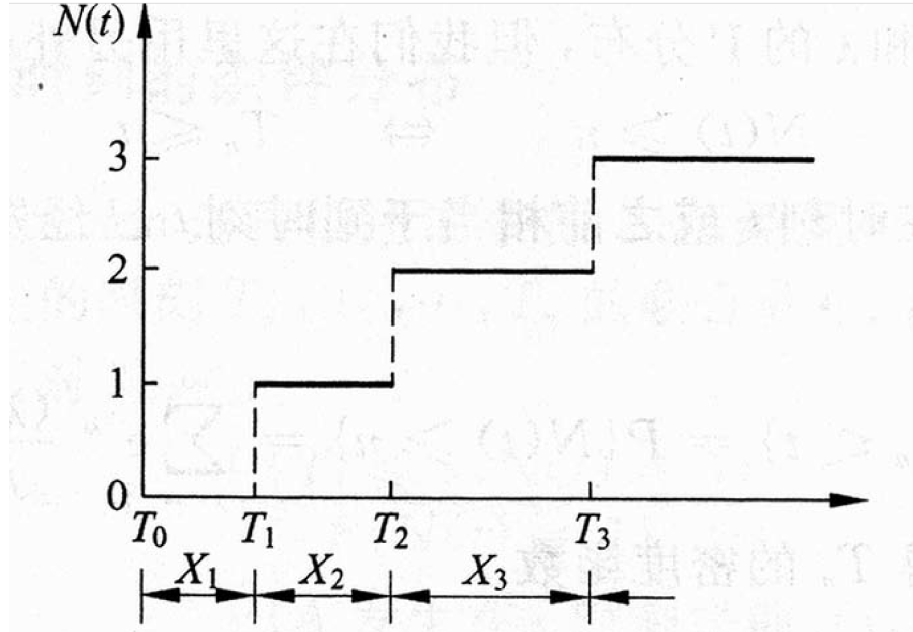
image-20240604220309463

Property

  1. 服从参数为的指数分布,且相互独立.
  2. 服从参数为和的分布;

事件发生时刻的条件分布

在已 知的条件下，事件发生的个时刻的联合概率密度是

Mark

  1. 如果知道事件只在内发生一次，那么发生的时刻服从均匀分布；
  2. 在已知内发生了次事件的前提下，各次事件发生的时刻 (不排序)可看做相互独立的随机变量，且都服从​上的均匀分布.

非齐次Poisson过程

当Poisson过程的强度λ不再是常数，而是一个时变参数时，Poisson过程被推广为非齐次Poisson过程。 计数过程称做强度函数为的非齐次泊松过程，如果

  2. 过程有独立增量；
  4. ​

等价定义如下：

  2. 过程有独立增量；

  3. 是参数为​ 的泊松分布.

Mark

泊松过程与非齐次泊松过程之间转换关系: 设是一个强度函数为的非齐次Poisson过程.对任意令,则 是一个强度为 1的泊松过程.

复合Poisson过程

随机过程被称为复合泊松过程，如果对于,可以表示为

其中是一个Poisson过程， 是一族独立同分布的随机变量，并且与​也是独立的.

Mark

  1. 常见应用：保险公司的索赔金额，顾客成批到达的排队系统

  2. 设 是 一 复 合 泊 松 过 程 , 泊 松 过程的强度为,则

    • 有独立增量；

    • 若,则E[X(t)]=\lambda tE(Y_1),\quad D[X(t)]=\lambda tE(Y_1^2).

    • 特征函数​

条件Poisson过程

Poisson过程描述的是一个有着“风险”参数λ的个体发生某一事件的频率。如果我们考虑一个总体，其中的个体存在差异，比如发生事故的倾向性因人而异，这时泊松过程的强度参数本身是一个随机变量.

设随机变量 如果在的条件下，计数过程是参数为的泊松过程，则称​为条件泊松过程.

设的分布是, 由 全 概 率 公 式 可 知 , 随 机 选 择 一 个 个 体 在长度为的时间区间内发生次事件的概率为

Property

设是条件泊松过程，且, 则