Planarity

一个平面图(planar)被定义为：在平面上绘制没有交叉的图；

若图不能在平面上绘制或表示，称为非平面图；

若两个图可以在同一个图的边插入一个2度的新顶点来获得，则这两个图是同胚的(homeomorphic);

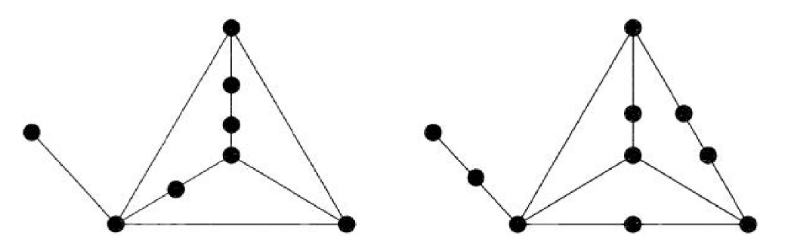
image-20241113203750619

称图紧缩于(contractible to)或， 如果我们将的边收缩能够得到，或;

Theorem(Kazimierz Kuratowski)

是非平面的；进一步地，如果一个图是平面图，当且仅当其没有子图和或同胚；

Corollary

一个图是平面的当且仅当它不包含可紧缩到或的子图;

proof:考虑命题反面

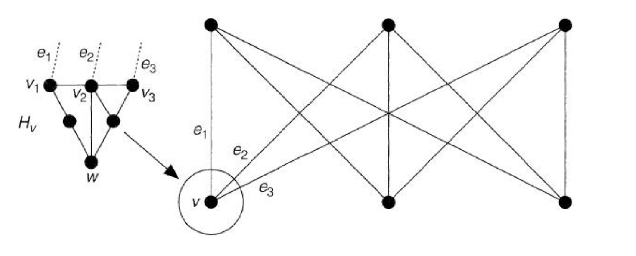
image-20241113204645054

Crossing

图的交叉数定义为将绘制在平面上是发生的最小交叉数；

显然;

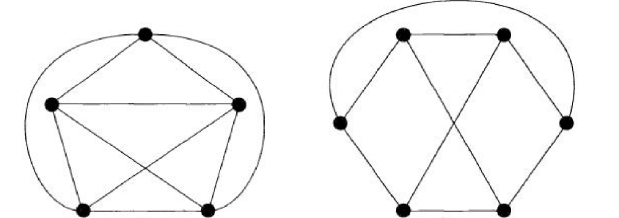
image-20241113205735583

图的厚度定义为将分解成若干个平面图的并的最小数量；

Theorem

对于简单图,顶点数,边数; 则厚度存在下界

proof:只需证;

Bound

定义一个平面图的区域的边界度(bound degree)为 为遍历区域的边界记录的图的边数；

假设平面图将平面划分为个区域，称为平面图的面数；

Theorem

假设平面图的面最小边界度为,则

对于不少于3个顶点的简单平面图，则

对于一般的平面图，自然有

对于二部平面图，有

Theorem(Euler)

若图是一个具有个顶点，条边和个面的连通平面图，则满足一下公式：

proof:若图有圈，删除一条圈中的边导致和均减少1，且不丢失连通性；重复上述操作划归为树的情况，即 note:由此可证明不是连通图；

Corollary

是平面图当且仅当;是平面图当且仅当;

Corollary

对于平面图，有

Polyhedra

一个多面体(polyhedron)定义为一个实体，它被有限个面包围，每一个面都是多边形； 一个多面体是凸的，若连接两个顶点的险段都完全包含在多面体内； 多面体可以用一个平面图表示；

一个多面体是正则的(regular)，若存在整数,每个顶点均有个面在此相遇，而且每个面的边界上均有条边；

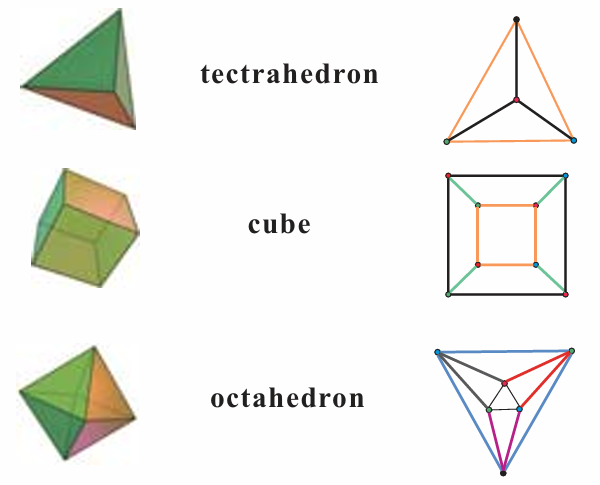
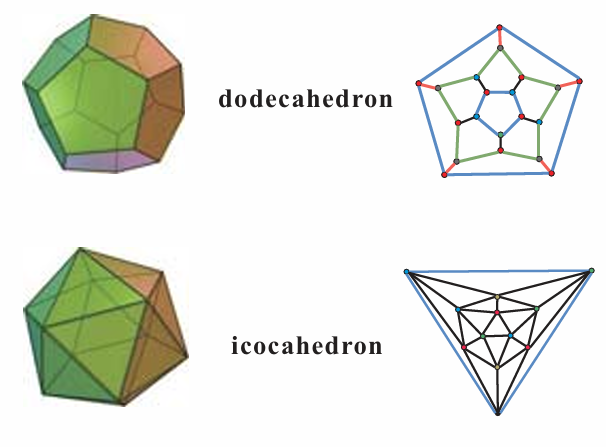
image-20250113201109956image-20250113201118879

Theorem

假定正多面体的顶点度为，每个面度为，则仅有如下取值：

proof:注意到

导出

Fullerene

一个烯(fullerene)的特征如下：

  • 由五边形和六边形构成；
  • 每个顶点处有3个面相遇；

可以确定，总共12个五边形；

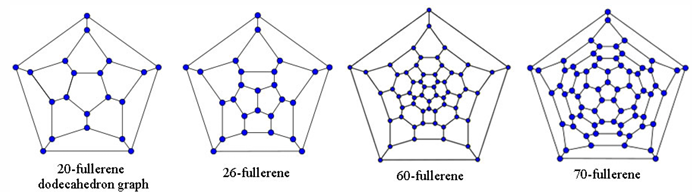image-20250113201045487proof:注意到

Genus

定义一个表面的亏格数(genus)，如果其拓扑同构于有个柄(handle)或者交叉帽(cross-caps)一个球体(sphere);

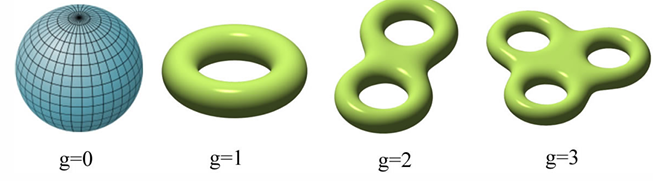
image-20250113201150372

这里给出结论，和是亏格数为1的图(toroidal graphs)；

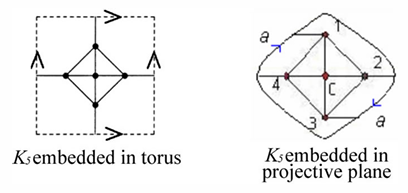
image-20250113201837423

Theorem

图的亏格数不超过其交叉数;

Theorem

对于可定向的连通图，亏格数为,顶点数为,边数为，面数为,满足

Theorem

对于不少于4个顶点的可定向的连通图，边数为,顶点数为，其亏格数满足