Matching

图中的极大匹配(maximal matching)是指不能添加更多的边的匹配；最大匹配(maximum matching)是指图中拥有最多边数的匹配；

  • 显然每个最大匹配都是极大的，反之未必；

给定匹配，一个-交替路径是指一个交替选择中的边和不在中的边的路径；一个-增广路径是指其两个端点不被浸润的-交替路径；

  • 给定-增广路径，我们可以替换中的边形成多一条的边的新的匹配;

对于定义在顶点集上的图,其对称差(symmetric difference)定义为顶点集为，边集中的边只属于和其中之一的图,通常具有异或(exclusive-or)性质；

对于两个匹配，;

对于二部图，一个完美匹配是指一个从到的一对一的对应关系使得每个具有对应关系的顶点都相邻；

结婚条件(Marriage condition)形象来说一组个女孩d至少总共认识个男孩；

Lemma

两个匹配的对称差的每个分量是偶圈或者路径；

proof：注意到;

Theorem(Berge)

图中的匹配是最大匹配当且仅当中没有增广路径；

proof: 充分性显然，下证必要性，若没有增广路径也不是最大匹配，取中的最大匹配，令，只包含偶圈和路径，注意到，必须包含一个分量是路径，其两个端点属于的边，这个路径就是的增广路径，矛盾；

Theorem(Hall)

对于二部图，存在到的完美匹配的充分必要条件是对任意子集，均有;

proof:这说明结婚条件是充分必要的；必要性显然，下证充分性

取中的最大匹配,没有浸润,我们说明存在子集使得;

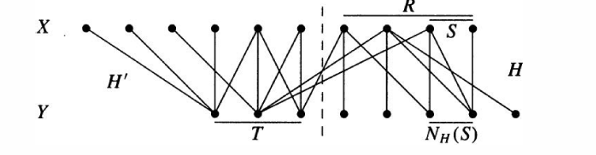
取且未被浸润,取通过交替路径到达的所有点中在的部分为,在中的部分为,注意有;

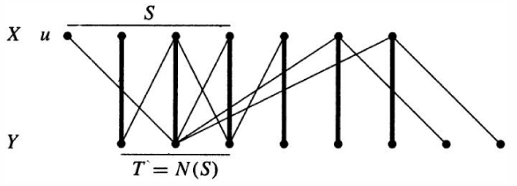
image-20250112155607024

  • 断言:匹配和

    每个在的顶点都可以通过中的一条边到达中顶点；没有增广路径因此中顶点都是浸润的，因此一个到达顶点的交替路径也通过的边到达，因此有

  • 由于，于是必有，故

由此证明了充分性；

也可以用归纳法证明；也可以使用Menger定理证明；

Corollary

对于-正则的二部图有完美匹配；

proof:统计边数验证满足结婚条件；

Theorem(Konig)

二部图中最大匹配数等于最小点覆盖数；

proof:相互构造

image-20250112162708568

Flow

称两条从到的路径是边不相交的(edge-disjoint)，如果它们没有公共边；

称两条从到的路径是点不相交的(vertex-disjoint)，如果它们没有公共点；

考虑图中不相邻的两个顶点，断集(vw-disconnected set)指图中的一个边集，每条从到的路径包括中的一条边；分离集(vw-seperated set)指图中的一个点集，每条从到的路径包括中的一条点;

一个网络(network)是一个带权有向图，每一条箭头分配一个容量；

一个流(flow)为每个箭头分配一个流量；

对于顶点，定义流出量为离开的箭头总流量，流进量为进入的箭头总流量；

称一个流是可行(feasible)，如果满足

  • 流量约束：对于每个箭头，；
  • 守恒约束：对于每个顶点，;

零流显然是可行，定义流的净流量/值为在汇点处

一个最大流是一个拥有最大净流量的可行流；

对于网络中的流，一个增广路径(f-augmenting path)是一个从源点到汇点的路径，在底图中的边满足如下性质：

  • 若在上同向，则,定义;
  • 若在上反向，则,定义;

称路径的容忍度(tolerance)为

一个增广路径对应一个大值流，这样的定义确保了容忍度为正；

一个s/t割(source/sink cut)由点集出发的到点集的箭头组成，构成点集的划分；

源/汇割的容量,是这些箭头的总容量；

一个最小割是指拥有最小总容量的割；

image-20250113154526967

Theorem(Menger)

连通图中相异顶点之间的边不相交路径最大条数等于不连通集的最少边数；

proof:显然后者不超过前者，只需证明前者不超过后者即可；

对边数归纳，考虑非平凡情况，假设图中最小的不连通集的边满足

  • 不是所有的边和相关联
  • 不是所有的边和相关联

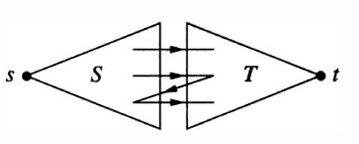
有两个分别包括顶点的不相交的子图;

定义为收缩中的每一条边形成的图，为类似收缩的每一条边形成的；由归纳假设，给出个边不相交的路径，所求的个边不相交路径显然就是给出的路径的并；

对于平凡情况，可以假设中每条边都在中，否则可以删去它使用归纳假设，考虑间的最短路，包括至多一条边在中；对采用归纳假设，至少有条边不相交路径，算上即可；

Theorem(Menger)

连通图中相异顶点之间的点不相交路径最大条数等于分离集的最少点数；

Corollary

对于图是-连通的当且仅当任意相异顶点之间有至少条边不相交的路径；

对于至少有个顶点的图，是-连通的当且仅当任意相异顶点间至少有个点不相交的路径；

值得一提的是，Menger定理对有向图也成立，因此一般表述成连通图中最大流等于最小割；手动添加两个顶点也可证明Hall定理；

Lemma

令是增广路径，具有容忍度，通过以下方式改变流

  • :在与同向的箭头上
  • :在与反向的箭头上

形成的新可行流，其值

Theorem(Max-flow Min-cut)

在任意网络中，最大流的值等于最小割的容量；

proof:容量为整数情形时可以看作Menger定理视作有向图中连接对应容量个箭头；

只需要找到一个流值等于一个割流量即可；

取为最大流，如下定义点集划分：点当且仅当存在路径使得或

由引理,源点,汇点;显然对每个,有,对于每个，我们有，否则应该属于;

因此有

是所求的最小割；

Algorithm(Ford-Fulkerson)

image-20250113171531290