Conceptions

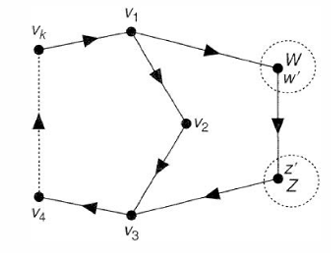
有向图(directed graph) 定义为非空有限顶点集和的有序对(箭头，arcs)形成的有限簇；

箭头的第一个顶点为尾(tail),第二个顶点为头(head)，箭头由尾指向头；

有向图消去方向后得到的无向图称作底图(underlying grapg)；

称为简单有向图(simple digraph)，如果 中所有箭头都不一样，且没有自环；

称两个有向图同构(isomorphic)，如果它们的底图同构且箭头保持相同的方向；

有向图的邻接矩阵定义为,为指向的箭头数；

关联矩阵定义为，如果是的尾,如果是的头；

有向图的迹是指箭头的有限序列；

称有向图为弱连通的，如果它不能表示为两个有向图的并，当且仅当其底图是连通的；

称有向图为强连通的，如果任何两个顶点.均有从到的有向路径；

有向图的强连通分量是其最大化的强连通子图；

称图为可定向的(orientable)如果图的每个边可以标定方向使得形成的有向图是强连通的；

称有向图是欧拉图，如果存在闭合迹包含中所有的箭头，这样的迹称作欧拉迹；

对于有向图的顶点,出度(out-degree)定义为以为尾的箭头数，入度(in-degree)定义为以为头的箭头数；

称顶点为有向图的源点(source)，如果;

称顶点为有向图的汇点(source)，如果;

称有向图是哈密顿的(Hamiltonian)，如果存在一个有向圈包括所有顶点；

称有向图是半哈密顿的(semi-Hamiltonian)，如果存在一个有向路径包括所有顶点；

Theorem(Robbin)

对于连通图，若是可定向的当且仅当是2-边连通的,即每条边至少被一个圈包含；

proof:必要性显然，充分性只需按照以下算法标方向即可：

  1. 选取任意一个圈,周期性地表明它的边的方向；

  2. 选取不在中但是和相关联的边；

    不是桥，假设被包含在中，令，回到1；

Theorem(Handshaking dilemma)

Theorem

连通有向图是欧拉的当且仅当对于中任何顶点均有;

Theorem(Ghouila-Houri)

令有向图是具有个顶点的强连通图；如果,则是哈密顿的；

Tourament

竞赛图(tourament)定义为任何两个顶点都有箭头相连的有向图；

Theorem(Redei)

任何非哈密顿的竞赛图都是半哈密顿的；(竞赛图必有哈密顿路)

proof：对顶点数归纳，取,由归纳假设，取路径，若或,直接加在头尾即可；否则存在是最小的满足的下标，则哈密顿路为;

Theorem(Moon)

竞赛图都是哈密顿的当且仅当是强连通的；

proof:必要性显然，充分性归纳证明更强结论：对于任意，存在长度为的圈；若当前圈之外存在一个顶点对圈既有出边也有入边，找到插入的下标即可得到更长圈；

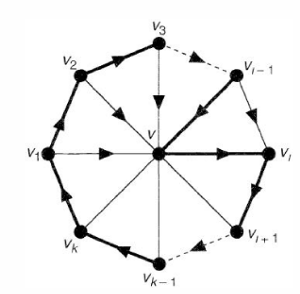
image-20250113204028589

否则可以划分为对圈只有出边和点集和对圈只有入边的点集,到必存在一条入边，考虑去掉圈中一点加入该边即可得到更长圈；

image-20250113204044553