Vertex Coloring

为图的每个顶点分配某种颜色，称一种着色是正确的，如果没有两个相邻的顶点着色相同；

一个独立集(independent set)是指内部没有任意两个点相邻的点集；

因此，在一个正确的着色中，位于不同独立集的点集可以被不同颜色着色；

一个-点着色的无环图可以被划分为个独立集;

图的一个-点着色是用个颜色对其顶点进行着色；若图是一个-点可着色的，如果图有一个正确的-点着色方式；

图的色数(chromatic number)等于最小的使得是-点着色的整数；

称图是-色(k-chromatic)图，如果;

确定一个图是否是3-可着色的是一个NPC问题，对于平面图，计算机已经证明四色定理：对于任何平面图均有;

对于给定的图确定色数是一个NP问题，但是色数有一个平凡上界;

Theorem

值得一提的是，Petersen图的色数为3；

Theorem

Proof:以下贪心算法是一种 正确的着色方案，这说明我们找到了色数的一个上界；

假设第个颜色记作,列举图的顶点;

  1. 为分配颜色;
  2. 对于状态,假定已经着色，分配颜色,为相邻顶点尚未使用的颜色最小下标；

等号在奇圈和完全图上成立；

Five-color Theorem

简单平面图是5-可着色的；

proof：对归纳，若,结论平凡，假设成立，考虑度数最小的点，一定有,由归纳假设，对于除去点的图存在着色方案，若，则的邻居一定为留出一个颜色；

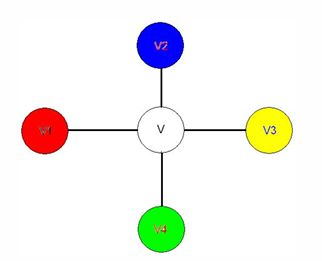
image-20250106184555304

考虑,记邻居顺时针方向为,若这5个点只用了4个颜色，剩下的颜色留给即可；若这5个点颜色各不相同，假设染1色，染2色，将改染1色，染1色的邻居改染2色，依次类推；

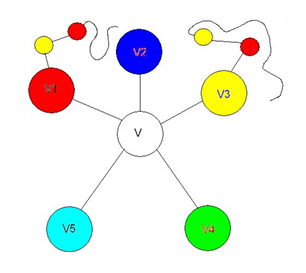
image-20250106184606381

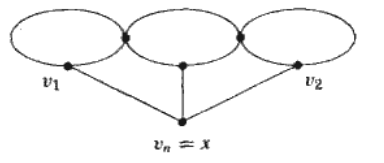
若这样的操作不i能持续下去，一定出现如下情况的子图

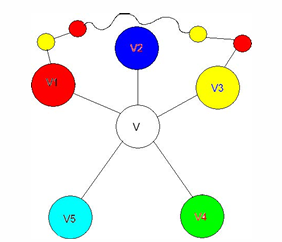
image-20250106184854521

由平面性，不会有这样的通路，对进行上述操作即可；

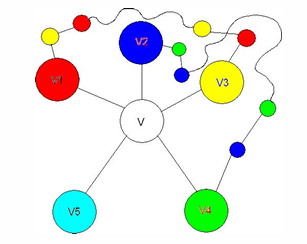
image-20250106185019264

进一步，我们有四色定理(Four-color theorem, Appel and Haken):任意简单平面图都是4-可着色的，即;

经过对偶图变换可以得知，世界地图可以用4种颜色进行染色；

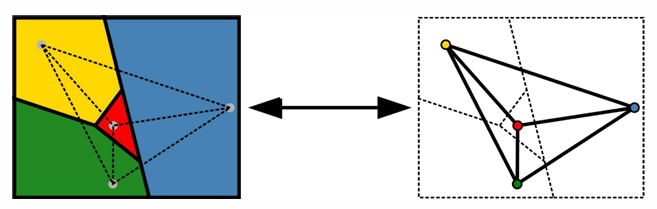
image-20250106185621087

Brooks Theorem

对于非奇圈的非完全的简单连通图,有;

proof：若存在度数小于的顶点，我们需要精心安排顶点的顺序，使得每个顶点在染色时，排在它前面并与之相邻的顶点数不超过,以为根的图生成树的后序遍历序列满足条件，因为除外，其余顶点在这棵生成树的父亲一定位于这个点序列的后面；

假设图是正则的；进一步假设；

若有割点，取图的割点，以及两个连通分量,取,且均是的邻居；

对于的任意连通分量，可以对进行着色，对这样方案下每个的着色顺序进行置换，使得他们在的颜色一致；

进一步假设，即是2连通的，断言图存在三个顶点,使得连通，且

先将染成同色，对于,考虑令,贪心地为其他点染色后，最后染时，由于有两个邻点同色，因此一定留有一种颜色；

下证明断言：若是3连通的，因为是正则且不完全的，故选取距离为2的两点和公共邻点即可；

若不是3连通的，但是是2连通的，由于没有割点，每个叶块均有的相邻顶点，由于，因此可以选取两个不直接相邻的叶块中与的邻点；

image-20250106201754800

Map Coloring

在地图着色问题中，不考虑地图之间的桥梁；

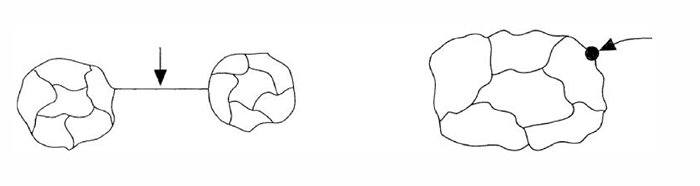
image-20250106202314043

定义地图(map)为一个3连通的平面图；

称一个地图是-面可着色的，如果它的面可以被个颜色着色且有公共边相邻的面颜色不同；

Theorem

地图是2-面可着色当且仅当是欧拉图；

proof：对于每个顶点，一定有偶数个围绕它的面(两种颜色的面个数相同)，意味着其度为偶数，为欧拉图

如果为欧拉图，则选取任意一个面染为红色，对于其他面，到的曲线穿过偶数条边染为红色，奇数条边染为蓝色，这样的染法是良定义的，因为每个顶点有偶数度

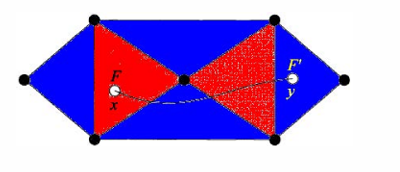
image-20250106203612297

Edge Coloring

图的一个-边着色是用个颜色对其边进行着色；

一个正确的边着色满足任意两个相关联的边颜色不同；

若图是一个-边可着色的，如果图有一个正确的-边着色方式；

不相关联的独立边集合称作一个匹配(matching)，更确切地说，在图中的一个匹配是一组互相没有公共顶点无环边集合，称顶点被匹配浸润的(saturated),若关联中的一条边，否则称为未浸润的(unsaturated);

一个正确的-边可着色可以认为对边集进行划分

其中是一个匹配，每个匹配分配相同的颜色；

边色数(edge chromatic number)定义为最小正整数使得为-边可着色的；

一个平凡下界为;

Theorem

对于奇数，任何匹配至多拥有条边，但是有条边，因此；

给出-边着色的构造：边界用种颜色染色，对角线的颜色和与之平行的边颜色相同；

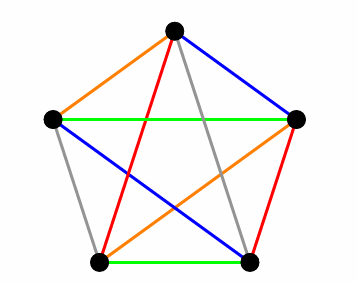
image-20250106231317930

对于偶数，我们给出-边着色的构造：

取出点,先为子图的用上述方案染色，每个顶点的关联边共种颜色，留下一个颜色与相连的边染色即可；

Theorem(Vizing)

对于有限图，两点间最大连边数为，则为-可染色的；

对于简单图来说，

Theorem(Konig)

对于二部图，

proof:对边数归纳，假设在较小的边数成立，考虑删除一条边，子图最大度不超过,对子图边染色，在子图中，,因此这样的边染色方案中，关联的边至少剩余一种颜色没有使用，设为，若,将染为该色即可；否则，考虑关联的染色的边,依次用色边增广它，得到增广路径不会经过点(因为没有奇圈)，反转增广路径的颜色后将染为色即为最终的染色方案；

Chromatic Polynomial

对于简单图，定义色数函数为将顶点用种颜色染色，相邻顶点不同色的方案数;

Theorem

对于简单图，有

proof:考虑删除一条边后的子图之间的关系，可以看作边顶点没有限制关系，可以看作边顶点必须同色；

显然是一个次多项式，满足如下性质

  • 系数正负交替；
  • 的系数是；
  • 常数项为0；