Brown运动
随机过程如果满足:
-
有平稳独立增量;
-
对 每 个, 服从正态分布;
则称为Brown运动,也称为Wiener过程.
等价定义如下:
- (正态增量)
- (独立增量)独立于过程的过去状态,
- (路径的连续性)是的连续函数.
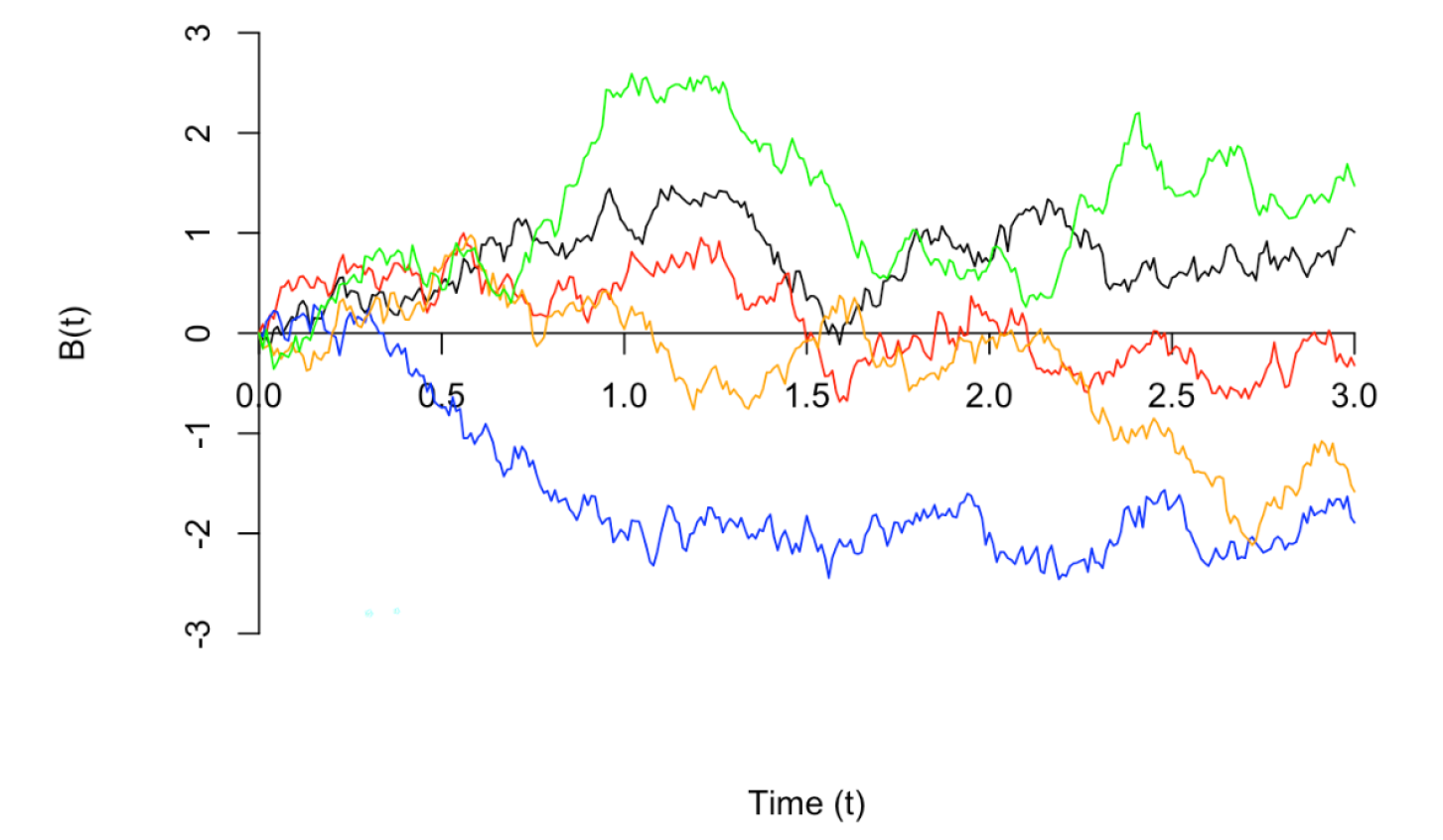
Property
- Brown运动是Gauss过程,
- Brown运动具有Markov性;
Mark
如果,我们称之为标准Brown运动。如果,则可考虑,它是标准Brown运动. 故不失一般性,可以只考虑标准Brown运动的情形。
等价定义并没有假定,因此我们称之为始于的Brown运动,所以有时为了强调起始点,也记为 ;
有限维分布
对于Brown运动,以及,有如下联合分布函数
即 的联合概率密度为
路径性质
对于Brown运动的一条样本路径, 几乎有如下性质:对区间遍取分割,且其模, 满足当极限的意义是依均方收敛;
-
是的连续函数;
-
在任意区间(无论区间多么小)上都不是单调的;
-
在任意点都不是可微的;
-
在任意区间(无论区间多么小)上都是无限变差的
-
对任意上的二次变差等于
以记Brown运动首次击中的时刻,即
对, 由 全 概 率公式
若,则在中的某个时刻击中,由对称性得
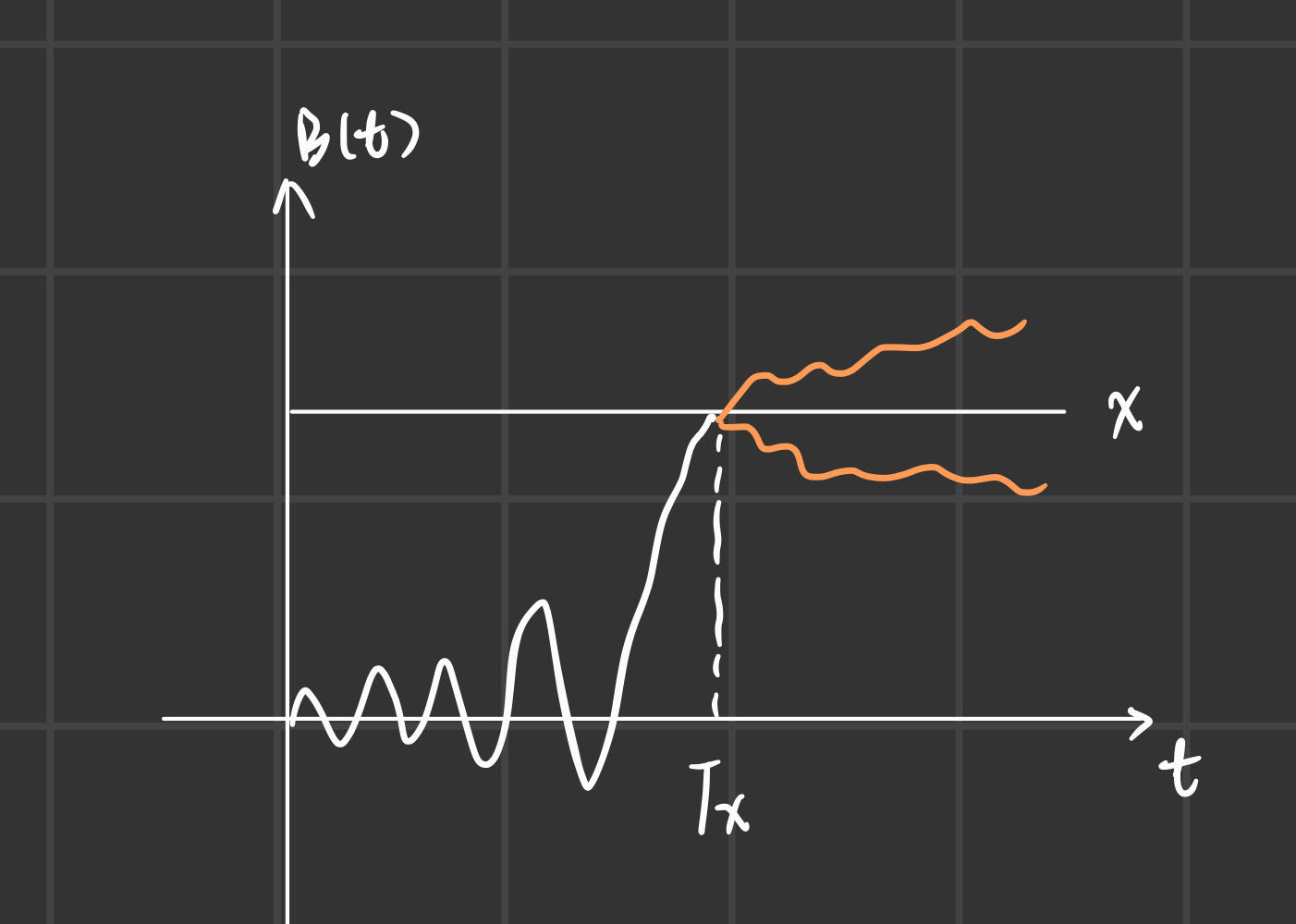
再由连续性可知,不可能还未击中就大于,
由此可见
性质称为Brown运动的常返性。
根据式(3),的分布函数和概率密度函数如下:
期望如下:
虽然几乎必然是有限的,但有无穷的期望.直观地看,就是Brown运动以概率1会击中,但它的平均时间是无穷的。
Brown运动的最大值变量
对Brown运动中在达到的最大值
其分布对有
而对于Brown运动在中达到的最小值, 当时 , 有
Brown 运动的反正弦律
设 为始于的Brown运动,则在中至少有一个零点的概率为
只需要知道Brown运动的最小值分布即可;
在区间中至少有一个零点的概率为
那么没有零点的概率为
证明:
取时刻之前的最后一个零点 \zeta_{t} = \sup{s\leq t,B(s)=0} 时刻之后的第一个零点\beta_{t} = \inf{s\geq t,B(s)=0}
由反正弦律有
Brown桥
设是Brown运动.令
则称随机过程为Brown桥。
Property
对
-
-
- Brown桥也是Gauss过程
有吸收值的Brown运动
设为Brown运动首次击中的时刻,
则是击中后,永远停留在那里的Brown运动。
离散部分的分布为
连续部分的分布:对
在原点反射的Brown运动
,则称随机过程为在原点反射的Brown运动.它的概率分布为
几何Brown运动
由 定 义 的 随 机 过 程 称 为 几 何 Brown运动。
由于Brown运动的矩母函数为,所以几何Brown运动的均值函数与方差函数分别为
在金融市场中,人们经常假定股票的价格按照几何Brown运动变化。
有漂移的Brown运动
设 是 标 准 Brown运 动 , 我 们 称 为 有 漂 移的Brown运动;
其中常数称为漂移系数。容易看出,有漂移的 Brown运 动 是 一 个 以 速 率漂移开去的过程;
对任意常数,记 为过程在击中之前击中的概率,有