退化分布(单点分布)
若随机变量只取常数,即
则并不随机,但我们把它看作随机变量的退化情况更为方便,因此称之为退化分布,又称单点分布.
离散均匀分布
若随机变量的分布律为
则称之为离散均匀分布,记作.
Property
- 特征函数
Bernoulli分 布
若 随 机 变 量的分布律为
则称之为离散均匀分布,记作Ber.
设事件出现的概率为,则为一次伯努利试验中出现的次数.
Property
- 特征函数
二项分布
若随机变量的分布律为
则称之为以和为参数的二项分布,记作.
设事件在每次试验中出现的概率均为,且每次实验相互独立,则为重伯努利试验中事件出现的次数.
Property
- 特征函数
几何分布
若随机变量的分布律为
则称之为几何分布,记作Geom.
在伯努利试验中, 设事件在每次试验中出现的概率均为,则为事件首次出现时的总试验次数;
Property
- 特征函数
Poisson分 布
若 随 机 变 量 的分布律为
其中,则称服从Poisson分布,记为Poi
Property
-
特征函数
-
数学期望
-
方差
负二项分布
对于任意实数,若随机变量的分布律为
则称之为负二项分布,记作。
Property
- 特征函数
在伯努利试验中,设事件在每次试验中出现的概率均为,则为直到事件成功次时,试验的总失败次数。
负二项分布通常用于替换Poisson分布。同Poisson分布一样,它也在非负整数上取值,但因为它包含两个参数,相比Poisson 分布其变化更灵活。Poisson分布的方差和均值相等,但负二项分布的方差大于均值.
Property
- 特征函数
连续均匀分布
如果的概率密度为
其中,则称之为区间上的(连续)均匀分布,记为
Property
- 特征函数
正态分布
如果的概率密度为
则称之为参数为和的正态分布,也称为高斯分布,记为
Property
-
若随机变量X服从正态分布,其中,的阶原点矩
证明
$E(X^k)=(k-1)E(X^{k-2}),E(X)=0$ -
特征函数
指数分布
如果的概率密度为
则称之为指数分布,记为Exp
Property
-
特征函数
-
分布函数
-
数学期望
-
方差
卡方分布
如果的概率密度为
为正整数,则称之为自由度为的卡方分布,记为
Property
-
特征函数
-
数学期望
方差
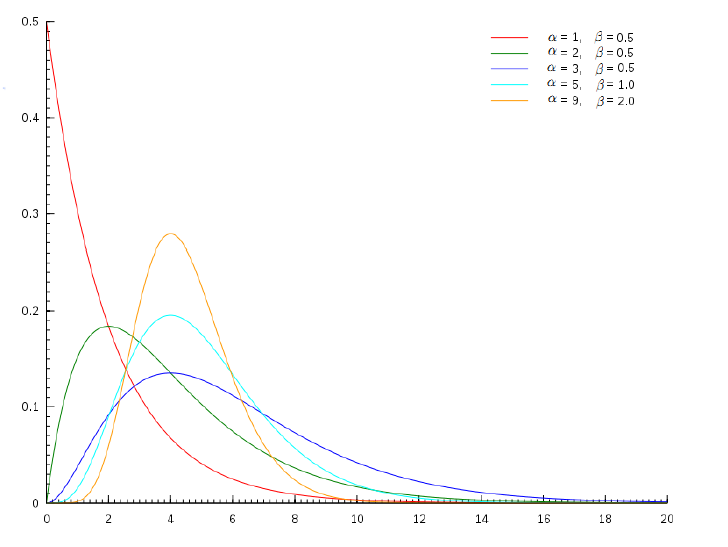
Γ 分 布
若的概率密度为
, , 则称服从形状参数,反尺度参数的分布,记为.
-
如果,对任意的
-
如果Exp,则
-
如果,则
-
如果相互独立同分布且服从参数为的指数分布,则
-
分布函数
-
特征函数
多维正态分布
设,是阶正定对称矩阵,并且其行列式为.如果的联合概率密度为
则称之为维正态分布,记为
Property
-
特征函数
-
若,则X的任一线性函数 服从维正态分布
-
若,则
-
设,并且与相互独立,则
其中均值,协方差矩阵
-
服从维正态分布当且仅当其任意非零线性组合
服从正态分布,其中不全为零.
-
特别的,对二位联合正态分布,其联合概率密度为
其中相关系数