Perceptron

Perceptron

线性可分

对于二分类问题，给定一个数据集

其中，。

如果存在一个超平面：能够将数据集中的正例和负例完全分开，即对于所有的正例有，对于所有的负例有，则称该数据集是线性可分的。

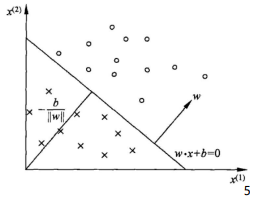
神经元

感知机(perceptron)是一种线性分类器，是最简单的ANN，只有一个神经元；

每个神经元作为独立的处理单元，模拟生物神经元行为的机器，有与生物神经元相对应的部件，如权重（突触）、偏置（阈值）及激活函数（细胞体），输出为+1或-1

• 对每个输入信号进行加权处理（确定其强度）；
• 确定所有输入信号的组合效果（求和）；
• 确定其输出（转移特性，即激励特性）。

感知机模型的假设空间是定义在特征空间中的所有线性分类器，形式化表示如下

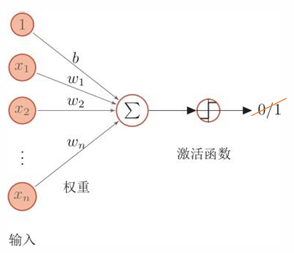
学习算法

感知机学习的目标是求得一个能够将训练集正实例点和负实例点完全正确分开的分离超平面。

感知机是一种错误驱动的在线学习算法

1. 初始化权重向量;
2. 每次分错一个样本时，即，使用该样本更新权重;

换而言之，感知机的损失函数如下，每次按梯度更新，学习率为1；定义全体误分类的点集为;

对于线性可分的数据集，感知机学习算法收敛，即经过有限次迭代可以得到一个将训练数据集样本完全正确划分的分离超平面和感知机模型。其迭代收敛性有如下Novikoff定理保证：

假设训练集线性可分，则存在满足的超平面能将数据集完全分开，且,对于所有训练样本有

感知机在数据集上的误分类次数存在上限

局限性

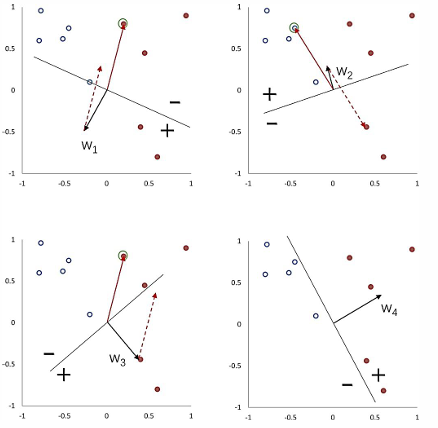
下图展示了感知机的参数学习更新过程。红色实心点为正例， 蓝色空心点为负例。黑色箭头表示当前的权重向量，红色虚线箭头表示权重的更新方向。

假设训练数据集线性可分，感知机学习的目标是求得一个能够将训练集正实例点和负实例点完全正确分开的分离超平面。

输入为的单层单个神经元（输入层不计入层数），采用阶跃激活函数，可以解决线性可分问题

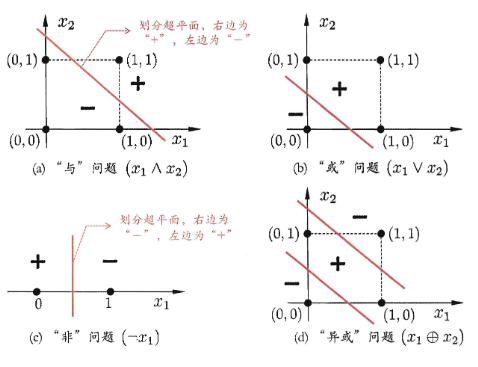
可以看到，单层感知机只能处理线性问题，无法解决异或问题，这是一类典型的线性不可分问题；

对偶形式

将参数反过来表示数据集的示例线组合，按照先前的学习方式

最后学习的参数具有如下形式

表示第i个实例点由于误分而进行更新的次数。实例点i更新次数越多，意味着它距离分离超平面越近，也就越难正确分类。换句话说，这样的实例对学习结果影响最大。

对偶形式中训练实例仅以内积的形式出现。为了方便，可以预先将训练集中实例间的内积计算出来并以矩阵的形式存储，这个矩阵就是所谓的Gram矩阵。