PCA

维度灾难

在一维的时候，数据点是非常稠密的，而随着维数的增加（如2维， 3维），整个数据点的空间就形成非常庞大的空间（由 3 个，变成9个，再变成27个），相应地，数据分布就变得相当稀疏了。

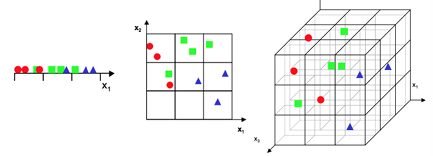
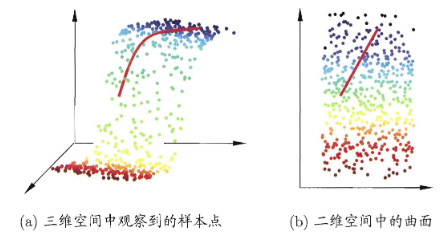
我们需要对原始高维空间转换为一个低维的子空间(subspace)，即降维；数据样本虽然是高维的，但与学习任务密切相关的也许仅是某个低维分布，即高维空间中的一个低维嵌入(embedding)；

主成分分析(Principal Component Analysis, PCA)作为一种典型的降维方法，旨在寻找一个超平面，满足如下性质

以下证明这两种性质等价；

假定对维空间的样本进行中心化；

投影变换的新坐标系为, 这些为标准的正交基,维度为；

新坐标系下，样本点变换为，反过来的坐标变换为;注意到

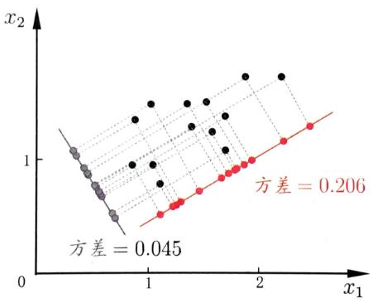
一种解释是最大可分性，我们的目标是投影在超平面上的点方差最大化，即

等价与最大化

另一种解释是最小重构性,期待最小化

计算重构前后的样本点集在低维空间的距离总和，目标使之最小

由Lagrange乘子法知，PCA的解析解为：将协方差矩阵特征值分解后的top d'个特征值对应的特征向量

算法流程对应如下

t-SNE是一种降维技术，用于在二维或三维的低维空间中表示高维数据集，从而使其可视化；

换而言之，t-SNE希望将一个高维数据集将其简化为一个保留了大量原始信息的低维图；通过保留局部邻域而不是全局距离来实现这一点。具体来说，t-SNE 关注的是：在高维空间中非常相似（距离很近）的点，在低维空间中也应该映射得很近；在高维空间中不太相似（距离较远）的点，在低维空间中也应该映射得较远。

首先，计算高维空间中任意两个数据点和之间的相似度。常用的方法是计算它们之间的欧几里得距离。将距离转换为条件概率 ，表示认为是其邻居的可能性。这个概率通常基于高斯分布（正态分布）来计算：

其中是以为中心的高斯分布的方差，即通过用户指定的困惑度(Perplexity)参数来确定。困惑度可以被理解为每个点周围的有效邻居数量。

为了得到一个对称的联合概率分布 P，t-SNE 使用

(这里的是数据点总数，分母是为了归一化)。这个表示和在高维空间中是邻居的联合概率。对于相距较远的点，的值会非常接近于零。

类似地，在低维嵌入空间中，我们为对应的映射点和计算它们之间的相似度。与高维空间不同，低维空间使用自由度为1的T分布来计算概率。低维空间中的联合概率定义为：

这里分母是为了归一化，确保所有的和为 1。

t-SNE 的目标是调整低维空间中的点的位置，使得低维概率分布尽可能地接近高维概率分布。t-SNE 使用梯度下降等优化方法来迭代调整低维点的位置，以最小化 KL 散度。损失函数的梯度为：