Naive Bayes 分类器
贝叶斯分类算法是统计学的一种分类方法,它是一类利用概率统计知识进行分类的算法。在许多场合,朴素贝叶斯(Naïve Bayes,NB)分类算法可以与决策树和神经网络分类算法相媲美,该算法能运用到大型数据库中,而且方法简单、分类准确率高、速度快。
但由于对数据特征条件独立的强假设,所以如果数据集不符合这种假设,准确率可能会较低。
Bayes决策论
假设有种可能的类别标记,即
先验概率是根据以往经验和分析得到的概率,我们用来代表在没有训练 数据前假设拥有的初始概率;
后验概率是根据已经发生的事件来分析得到的概率。以代表假设成 立的情下观察到数据的概率,因为它反映了在看到训练数据后成立的置信度;
是将一个真实标记为的样本误分类为所产生的损失.
基于后验概率可获得将样本分类为所产生的期望损失;
即在样本上的"条件风险"(conditional risk)
我们的任务是寻找一个判定准则以最小化总体风险
对每个样本,若能最小化条件风险,则总体风险也将被最小化.
若目标是最小化分类器错误率,则误判损失表示为\left.\lambda_{ij}=\left{\begin{array}{ll}0,&\mathrm{if~}i=j:;\1,&\mathrm{otherwise},\end{array}\right.\right.
此时条件风险 ,
于是,最小化分类错误率的贝叶斯最优分类器为
即对每个样本,选择能使后验概率最大的类别标记(hard assignment),这就是最小错误概率分类准则等价于最大后验概率分类准则;
属性条件独立假设
假设有维属性数目,
由极大似然估计可知,贝叶斯判定准则如下:
拉普拉斯修正
为了避免其他属性携带的信息被训练集中未出现的属性值"抹去", 在估计概率值时通常要进行"平滑"(smoothing)
避免了因训练集样本不充分而导致概率估值为零的问题,
并且在训练集变大时,修正过程所引入的先验(prior)的影响也会逐渐变得可忽 略,使得估值渐趋向于实际概率值.
极大似然估计
Idea
贝叶斯学派认为参数是未观察 到的随机变量,其本身也可有分布,因此,可假定参数服从一个先验分布,然后 基于观测到的数据来计算参数的后验分布;
MLE 认为,我们已经观测到的数据是最可能出现的数据。因此,我们应该选择那些参数值,使得这些观测数据出现的概率(或概率密度)达到最大。
似然函数估计
对于给定的参数 和一组独立同分布观测数据 ,这些数据联合出现的概率是各个数据点概率的乘积:
我们将这个概率视为关于参数 的函数,称为**似然函数 **(Likelihood Function)
注意,这与概率密度函数不同,概率密度函数是将 作为变量, 作为常数;而似然函数是将 作为变量, 作为已知的观测数据。
为了简化计算,通常改写对数似然函数(Log-Likelihood Function):
由于对数函数是单调递增的,最大化 与最大化 是等价的。
MLE 的目标就是找到使似然函数 达到最大值的参数 。即:
令偏导数等于零,解这个方程组以找到参数 的估计值。如果解析解难以获得,可以使用数值优化方法(如梯度下降)来最大化 。
EM算法
在无监督学习或者半监督学习中,数据没有标签,可以认为它们是未观测的隐变量(latent variable);
令为已观测的变量集,表示隐变量集,为模型参数,改用对作极大边际似然(marginal likelihood)估计
流程
EM 算法是一个两步迭代过程,直到参数收敛:
E 步 (Expectation Step):
- 模型参数是已知的,根据训练数据推断出最优隐变量的值。
- 利用当前的参数,计算每个数据点属于每个隐变量状态(或簇)的后验概率或称为"责任"。
- 本质上基于推断
M 步 (Maximization Step):
- 假设在 E 步计算出的隐变量的后验概率是已知的,基于这些后验概率(即隐变量的软分配),重新估计模型参数;
- 以最大化观测数据的完全数据对数似然的期望(这里的期望是在 E 步计算出的隐变量后验分布下计算的)。
- 基于和,对作MLE;
朴素贝叶斯分类器
朴素贝叶斯分类器(Naive Bayes Classifier)是一种基于贝叶斯定理和特征条件独立性假设的概率分类算法。它是一种简单但非常有效的分类方法,在许多实际应用中表现良好。
核心原理
朴素贝叶斯分类器基于贝叶斯决策论中的最大后验概率 (MAP) 原则。给定一个样本 ,我们希望预测它属于哪个类别 的概率最大,即找到:
根据贝叶斯定理,后验概率 可以写成:
先验概率已知,引入属性条件独立假设,只需最大化分子即可:
假设是训练集中第c类样本组成的集合,取值为的样本集合为可根据独立同分布样本估计
对于连续属性可假设为正态分布;
为了避免在估计条件概率时出现概率为零的情况(例如,某个特征值在训练集中某个类别下从未出现过),通常采用拉普拉斯修正进行"平滑"。这会在分子和分母中都加上一个小的常数(通常是 1),避免了概率估计为零对整个乘积造成影响。
参数估计
模型中的参数 和 需要从训练数据中估计。通常使用MLE来进行估计:
- 类别先验概率 估计为训练集中属于类别 的样本占总样本数的比例。
- 条件概率 估计为在属于类别 的样本中,特征 取值为 的样本占该类别样本总数的比例。
优点
- 简单高效: 算法逻辑简单,易于实现,计算速度快。
- 对小规模数据和高维数据有效: 在训练数据量不是非常大时也能表现良好。
- 对缺失数据不敏感,鲁棒性强: 可以相对容易地处理缺失数据(例如,在计算概率时忽略缺失的特征)。
缺点
- 特征条件独立性假设在实际中往往不成立,这可能会降低分类性能。当特征之间存在强相关性时,朴素贝叶斯的性能可能会受到影响,尤其在图像或语音等任务中精度不佳。
- 对连续型特征的处理需要进行离散化或假设特定的概率分布(如高斯分布)。
- 无法捕捉特征之间的交互作用: 不能建模特征之间的协同效应。
- 概率估计不总是可靠: 尤其是当某些组合在训练集中未出现时(可用拉普拉斯平滑缓解)
Bayesian Network
Idea
贝叶斯网(Bayesian Network)是一种概率图模型,它通过 (DAG)来描述一组随机变量之间的条件依赖关系。
- 图中的节点表示随机变量。
- 图中的有向边表示变量之间的直接依赖关系。如果从变量 A 指向变量 B 有一条边 (),则表示在知道 A 的值后,B 的概率分布可能会发生变化,即 B 直接依赖于 A。
注意: 边表示因果或影响关系,但不一定是严格的因果关系。
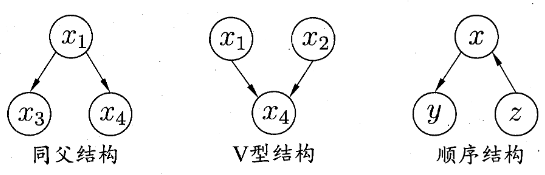
- 在同父结构中,给定父结点的取值,则 X3 与 X4 条件独立.
- 在顺序结构中,给定 z 的值,则 u 与 z 条件独立 .
- v 型结构,给定子结点 X4 的取值, Xl 与 X2 必不独立; 若X4的取值完全未知,则 V 型结构下 Xl 与 X2 却是相互独立的.(边际独立性)
条件概率分布
每个节点 都有一个与之关联的 CPD,它描述了在给定其所有父节点状态下的概率分布(Conditional Probability Distributions, CPDs)。
- 如果一个节点没有父节点,它只有一个先验概率分布。
- 对于节点 及其父节点集合 ,其 CPD 表示为
贝叶斯网的关键在于,图的结构和 CPDs 可以用来唯一地确定所有变量的联合概率分布。对于贝叶斯网中的一组变量 ,它们的联合概率分布可以分解为每个变量在其父节点条件下的概率的乘积:
这个公式是根据**图的结构(独立性假设)**得出的。具体来说,每个变量在其父节点已知的情况下,条件独立于其非后代节点。
朴素贝叶斯是具有特定图结构(中心一个类别节点指向所有特征节点)和特定独立性假设(特征之间在类别条件下相互独立)的贝叶斯网。
推断与学习
贝叶斯网的主要任务包括:
推断 (Inference): 在已知部分变量的观测值(证据)下,计算其他未知变量的后验概率。
学习 (Learning):
- 结构学习 (Structure Learning): 从数据中学习变量之间的依赖关系,即学习图的结构。
- 参数学习 (Parameter Learning): 在图结构已知的情况下,从数据中估计每个节点的 CPDs。