LDA技术
Idea
对于一类二分类问题,还可以采取线性判别分析(Liner Discriminant Analysis);
给定训练样例集,将样本投影到一条直线上,使得同类顶点尽可能接近,一类样本投影点尽可能远离;
同类点协方差尽可能小,异类中心距离尽可能大;
对新样本分类时,将其投影到该直线上,根据投影点的位置判定类别;因此LDA可以被视作监督降维技术;
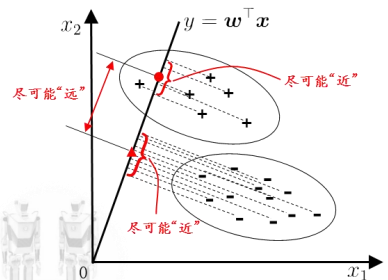
二分类问题
对于二分类问题,假设两类样本的集合分别为 和 ,它们的均值向量分别为 和 。其协方差矩阵为;
在投影到 方向后,两类样本的均值分别为 和 ;投影后的协方差矩阵变为和;
定义类内散度矩阵
投影后样本的类内总散度为 。
定义类间散度矩阵
投影后两类样本的均值差的平方为
进一步定义全局散度矩阵为;
LDA的目标是最大化类间散度同时最小化类内散度,这可以表示为最大化以下目标函数 :
这个目标函数就是广义瑞利商(Generalized Rayleigh Quotient)的形式。
转化为一个最优化问题,取分母为1,等价于
采用Lagrange乘子法,得到如下的广义特征值问题:
即最大化广义瑞利商的问题可以转化为求解一个广义特征值问题;
如果 是可逆的(通常情况下需要满足样本维度小于样本数量,并且各个特征之间不是完全线性相关的)
因此,最优的投影方向 对应于矩阵 的最大的非零特征值所对应的特征向量。对于二分类问题, 的秩最大为1,因此最多只有一个非零特征值。
对于不可逆的情况,考虑对作奇异值分解;
结果为
通常在计算时,为了数值稳定性,会先对数据进行白化处理。
对于不可逆的情况,考虑对作奇异值分解;
多分类问题
LDA可以自然地推广到多分类问题。假设有 个类别,类别 的样本集合为 ,均值向量为 。
LDA的目标是找到一个投影矩阵 ,将样本从原始 维空间投影到 维子空间中,使得投影后的样本具有最大的类间可分性和最小的类内方差。通常,投影后的维度 最大为 。
多分类类内散度矩阵:
这里, 是第 类样本的均值向量。
多分类类间散度矩阵: 假设总样本均值为 ,其中 是总样本数。第 类样本数为 。
多分类LDA的目标是找到一个投影矩阵 (其列向量是投影方向),使得投影后的类间散度尽可能大,类内散度尽可能小。这通常通过最大化以下目标函数来实现:
最大化这些目标函数等价于求解以下广义特征值问题:
最优的投影矩阵闭式解 由与最大的 个非零特征值 对应的特征向量 组成,即