数据结构

K-Dimensional Tree (KD-Tree) 是一种用于组织 k 维空间中的点的数据结构，主要用于快速进行范围搜索和最近邻搜索。它可以看作是二叉搜索树在多维空间上的扩展。其结构非常适合寻找最近邻居和碰撞检测.

KD-Tree 的核心思想是通过一系列与坐标轴平行的超平面，将 k 维空间递归地分割成更小的区域。每个区域对应于树的一个节点，存储该区域内的一个数据点。

KD-Tree 是一棵二叉树。

  • 节点: 每个节点包含一个 k 维数据点、一个用于分割空间的维度 (split dimension) 和一个分割值 (split value)。
  • 子节点 (Children): 节点的左子树包含该分割维度上值小于等于分割值的点，右子树包含值大于分割值的点。

构建 KD-Tree

构建 KD-Tree 是一个递归过程：

  1. 选择分割维度: 在当前节点的数据集中，选择一个维度用于分割。通常，这个维度是根据树的层级确定的，第0层从方差大的维度开始切分，然后循环选择其他维度；
  2. 选择分割值: 在选定的分割维度上，找到数据集的中位数作为分割值。将中位数点作为当前节点存储的点。
  3. 划分数据集: 根据分割值，将数据集中的点分成两部分：小于等于分割值的点构成左子集，大于分割值的点构成右子集。
  4. 递归构建子树：对左子集和右子集分别递归地构建左子树和右子树。

这个过程持续进行，直到数据集为空或只剩下一个点（作为叶子节点）。

复杂度: 构建一个平衡的 KD-Tree 的时间复杂度通常是 ,然而，在最坏情况下可能会退化。

image-20250528112430277

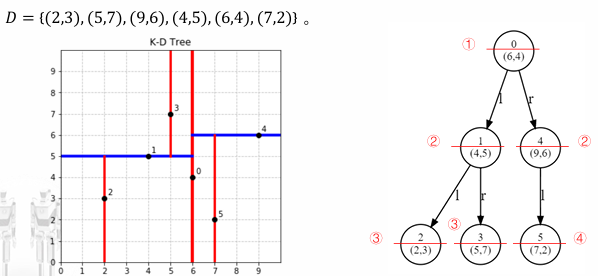
范围搜索

查找落在指定多维区域（例如一个矩形或球体）内的所有数据点。

  • 从根节点开始。
  • 如果当前节点的分割超平面与查询区域相交，则需要同时搜索左右子树。
  • 如果查询区域完全位于分割超平面的某一侧，则只需要搜索对应的一侧子树。
  • 当到达叶子节点时，检查该点是否在查询区域内。
  • 剪枝：如果在某个节点，发现以该节点分割值和维度确定的区域完全不在查询区域内，则可以剪掉整个子树。

最近邻搜索

输入：构造好的KDTree，目标样本;

输出：样本的最近邻；

过程：

  1. 从根节点开始，沿着查询点在每个分割维度上的值，从根结点出发，递归地向下访问𝑘𝑑树，维护当前最近邻点的样本值；

    • 若目标点𝑥当前维的坐标小于切分点的坐 标，则移动到左子结点;
    • 否则移动到右子 结点。直到子结点为叶结点为止。
    • 将该叶子节点作为当前的最近邻点，并记录其距离。

    image-20250528111415217

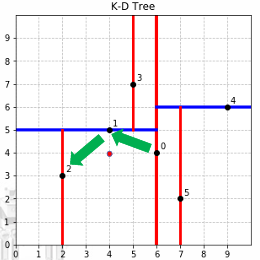
  2. 回溯与剪枝 在递归返回的过程中，对于当前节点，检查是否有可能在另一个子树中找到更近的邻居。在回溯过程中，不断更新最近邻点和距离。

    • 计算查询点到当前节点分割超平面的距离。

    • 如果这个距离小于或等于当前找到的最近邻距离，则需要进入另一侧的子树进行搜索。

      image-20250528112125552

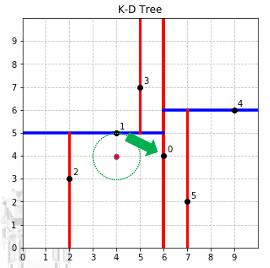
    • 如果这个距离大于当前找到的最近邻距离，那么另一侧的子树中不可能存在更近的点，可以剪掉该子树，不需要进入搜索。

      image-20250528112210081

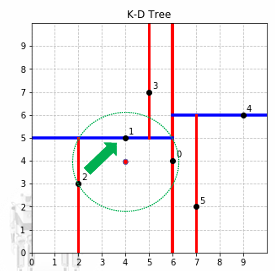
  3. 当回退到根结点时，搜索结束。

复杂度: 平均情况下，最近邻搜索的时间复杂度是。但在高维空间（k 很大）下，KD-Tree 的性能会急剧下降，搜索可能需要访问树的大部分节点，趋向于 (O(N));

特点

  • 维度诅咒: 在高维空间下性能显著下降。对于高维数据，其他方法如 Ball Tree 或局部敏感哈希可能更有效。
  • 树的平衡性: 随机插入和删除操作可能导致树失去平衡，影响搜索效率。虽然可以通过周期性地重建树来解决，但这会增加开销。
  • 对数据分布敏感: 如果数据在某些维度上高度集中，树可能会变得不平衡。