idea

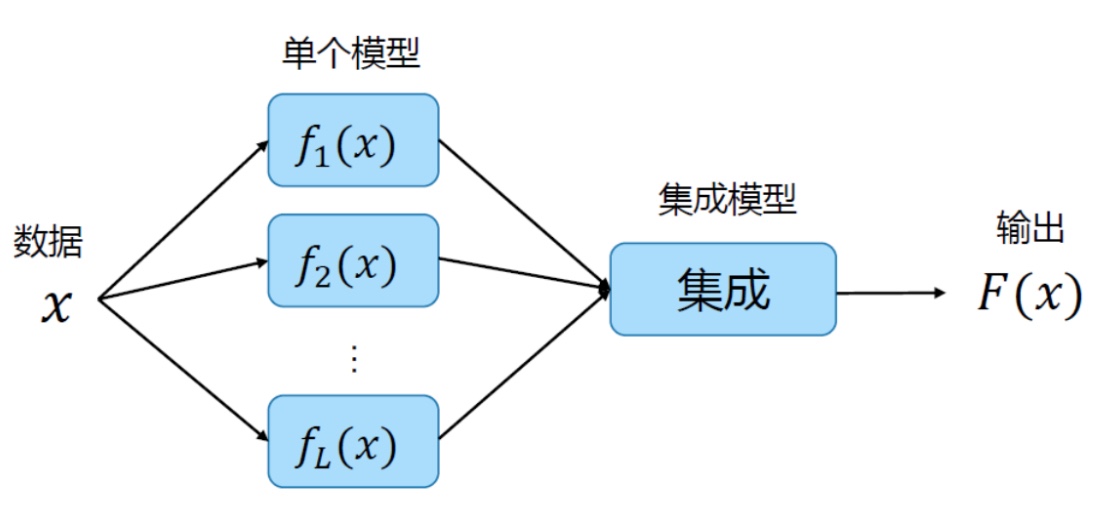
集成学习 (ensemble learning) 通过构建并结合多个学习器来完成学习任务。 下图展示了集成学习的一般结构：

  1. 先产生一组个体学习器 (individual learner)作为参与集成的学习器单元,不同预测模型在数据上具有不同表现
  2. 再用某种策略将它们结合
    • 若集成中只包含同种类型的个体学习器，这样的集成是同质的(homogeneous)；同质集成中的个体学习器称为基学习器(base learner); 相应的学习算法称为基学习算法(base learning algorithm)；
    • 集成也可以包含不同类型的个体学习器，即异质的 (heterogenous)或组件学习器；

集成学习框架

特征

集成学习通过将多个学习器进行结合，通常可以获得比单一学习器显著优越的泛化性能。这对弱学习器(weak learner) 尤为明显。 弱学习器：预测结果比随机猜测略好的学习模型； 强学习器：预测结果明显比随机猜测好的学习模型；

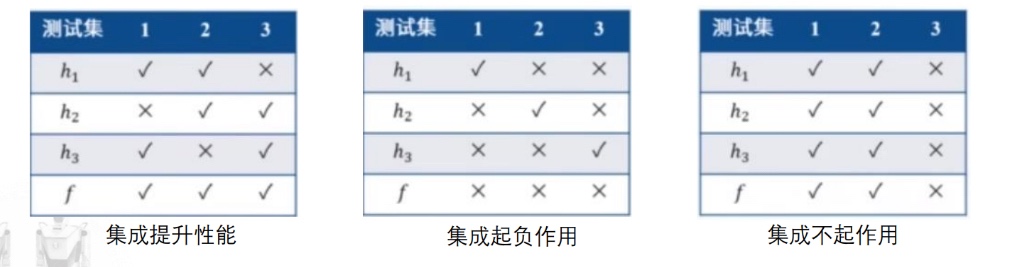
实际中，成功的集成要求个体学习器通常应该好而不同，

  • 准确性：个体学习器要有一定的准确性；
  • 多样性：学习器间具有差异，预测模型犯的错误不相同，鼓励集成不同类型；

集成模型的特征

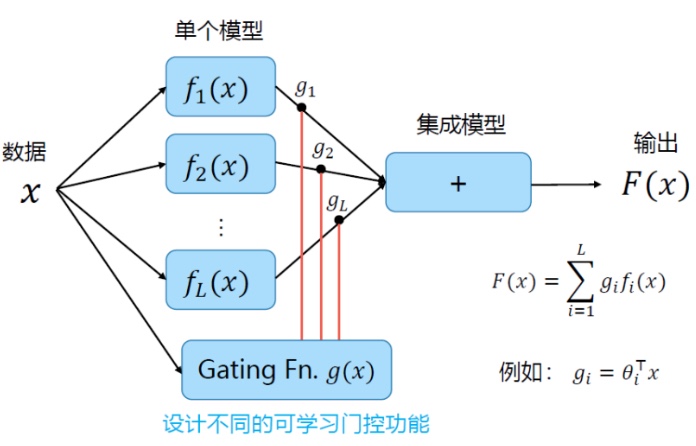
组合模型

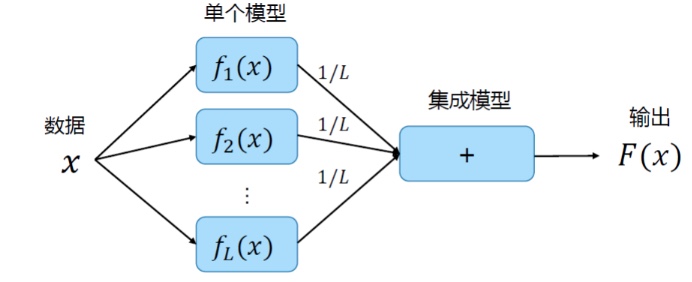
实际操作一般有如下方式集成 平均：回归问题求平均值，分类分题进行投票

，

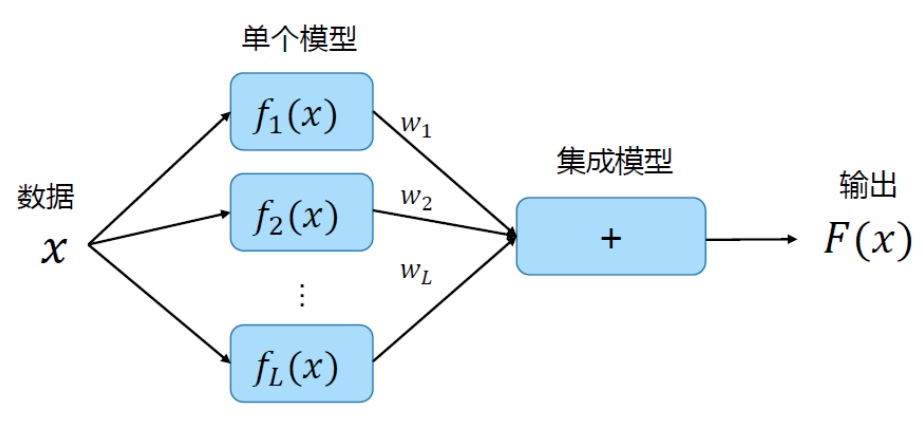
加权平均：训练集成模型时更新所有模型;

，

门控：训练集成模型时更新所有模型，比如自动驾驶中面对复杂的不同场景，切换不同的模型

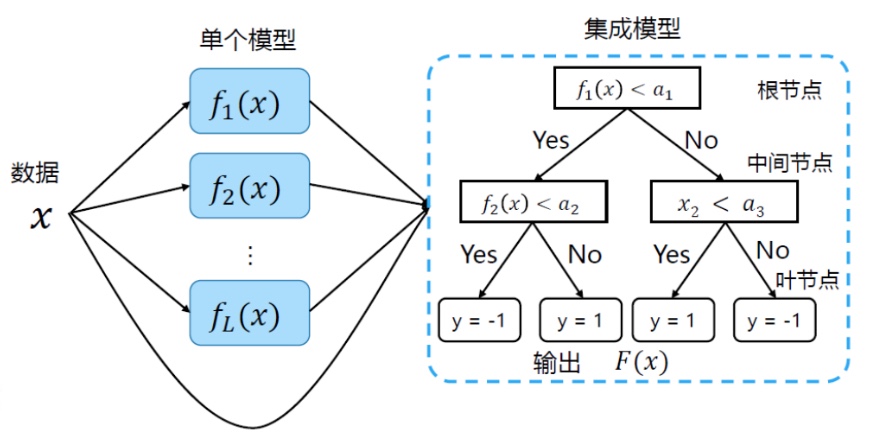
树模型：用决策树作为集成模型，根据和函数的值进行结点拆分

策略

成功的集成学习西药一些多样性策略

  • 包含不同类型的预测模型：比如识别pattern比较困难
  • 改变训练集：数据过拟合
  • 改变特征集：特征具有噪声
  • 数据处理：避免学习到的集成模型过拟合

​

Bagging

Bagging策略

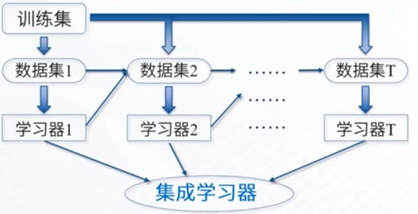
Bagging是一种并行学习策略，从原始样本集中生成不同的子集

  1. 给定包含 m个样本的数据集，先随机取出一个样本放入采样集，再把该样本放回初始数据集，使得下次采样时该样本仍有可能被选中；
  2. 经过 m 次随机采样，得到含 m 个样本的采样集；
  3. 初始训练集中有的样本在采样集多次出现，有的则从未出现；

这样可采样出 T 个含 m 个训练样本的采样集，然后基于每个采样集训练出一个基学习器，再将这些基学习器结合。这就是 Bagging 的基本流程。 核心问题为保证个体学习器采用不同的训练集，即子集生成问题

  • 若子集与原始集合偏离过多，则基学习器经验风险过大；
  • 若两个子集重叠样本过多，则基学习器过于相似；

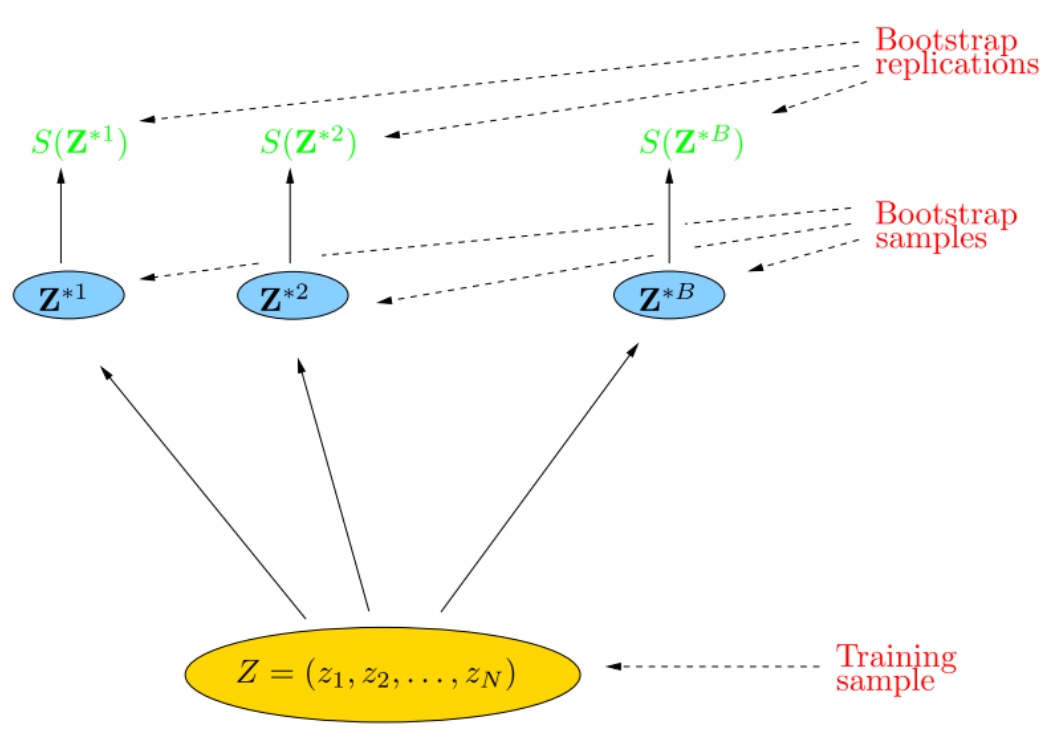
Bootstrap策略

Bootstrap策略是一种有放回的均匀抽样

  • 每个个体分类器的每次采样均从N个样本的原始数据抽取，从训练数据中有放回地采样生成一些数据，每个复制数据集大小和训练集相同

  • N无穷大时，样本未被抽到的概率为

复制数据集上的评估方差

模型误差

由于数据实例在自举采样数据集出现的概率约为0.632；直接在训练集上验证，大概率会过拟合； 因此提出留一自举法(leave-one-out bootstrap):构建自举复制集时不采样实例，然后利用这个实例评估模型

其中是那些没有包含实例的自举复制集的索引集合；如果为空集则忽略这些情况；

最后集成这些自举数据集上的模型，采用Bootstrap Aggregating(B-gag-ing)自举复制

  • 对于有个训练样本的数据集
  • 通过有放回的采样构造新的数据集
  • 构造个自举采样集;
  • 训练预测模型集合; 最终的预测结果为模型平均值

Pasting策略

Pasting策略时一种无放回的均匀抽样

  • 对于每个个体分类器，已经抽出的样本不再出现
  • 个体分类器的训练样本一般占总样本的60%到80%，，一般无重复

有效性分析

以下为两种场景的Bagging算法的分类效果

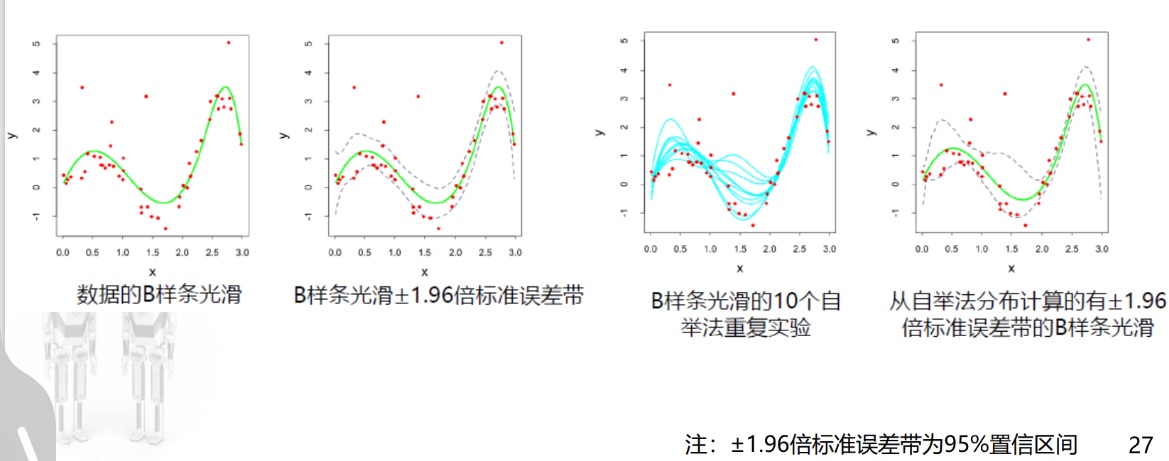
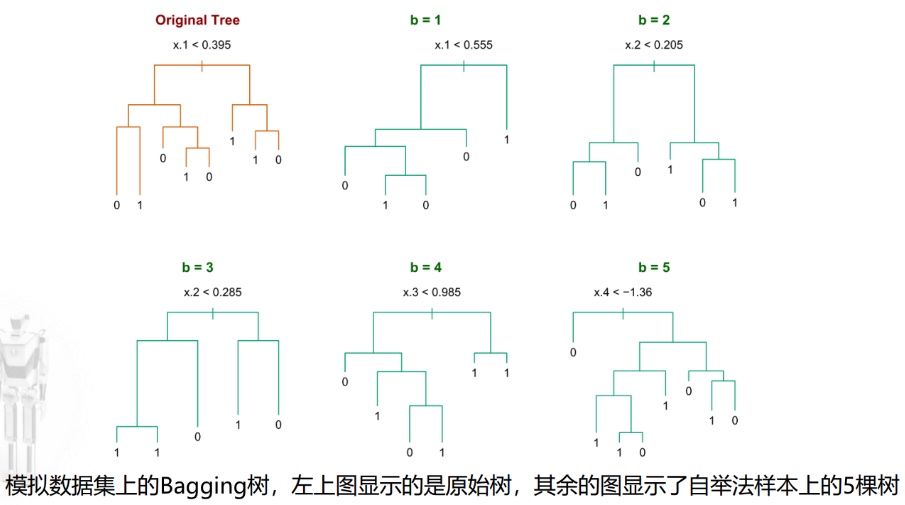
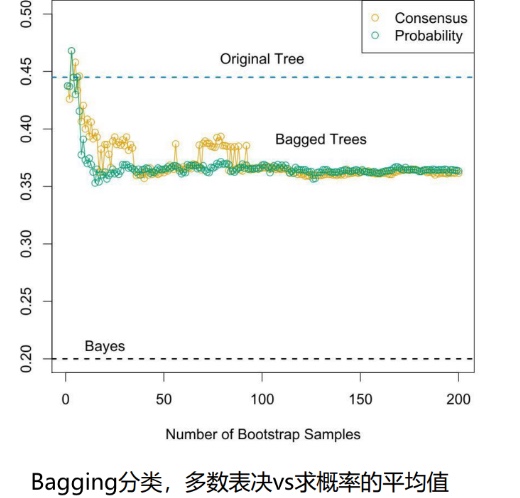
Bagging后的集成模型偏差和原始模型相同，但是降低了反差，对低偏差高反差的预测模型的提升效果显著；

对一系列服从同一分布的随机变量，方差为,两两关联性为,它们的均值变量方差为

随机森林

随机森林 (Random Forset，RF) 是 Bagging 的一个扩展。RF构建了一个解耦合(decorrelated)的树，然后对结果取平均。

RF 在以决策树为基学习器构建 Bagging 集成的基础上，在决策树的训练过程中引入随机属性选择。

  • 传统决策树在选择划分属性时是在当前节点的属性集合 (假定有 d 个属性) 中选择一个最优属性；
  • 在 RF 中， 对基决策树的每个结点，先从该结点的属性集合中随机选择一个包含 k 个属性的子集，然后再从这个子集中选择一个最优属性用于划分；
  • 参数 k 控制了随机性的引入程度。 一般取,甚至为1；

算法流程如下

  1. 假如有N个样本，则有放回的随机选择N个样本(自举采样：每次随机选择一个样本，然后返回继续选择)。这选择好了的N个样本用来训练一个决策树，作为决策树根节点处的样本。
  2. 当每个样本有M个属性时，在决策树的每个节点需要分裂时，随机从这M个属性中选取出m个属性，满足条件m << M。然后从这m个属性中采用某种策略（比如说信息增益）来选择1个属性作为该节点的分裂属性。
  3. 决策树形成过程中每个节点都要按照步骤2来分裂（很容易理解，如果下一次该节点选出来的那一个属性是刚刚其父节点分裂时用过的属性，则该节点已经达到了叶子节点，无须继续分裂了）。一直到不能够再分裂为止。注意整个决策树形成过程中没有进行剪枝。
  4. 按照步骤1~3建立大量的决策树，这样就构成了随机森林了

假设集成结果为,可以做回归预测平均值，也可以分类进行多数投票；

  • Bagging仅仅是在有相同权重的自举采样集上对每个预测模型进行训练 ；
  • 随机森林通过采样特征的方法尝试去解耦合自举训练预测模型（决策树）；
  • Boosting算法基于之前的预测模型有策略性地学习和结合接下来的预测模型；

Boosting

Boosting 是一族可将弱学习器提升为强学习器的算法：先从初始训练集训练出一个基学习器，再根据基学习器的表现对训练样本进行调整，使得先前基学习器做错的训练样本在后续受到更多的关注，然后基于调整后的样本训练下一个基学习器，如此重复进行，直至基学习器达到事先指定的值，最终将这 T 个基学习器进行加权结合。

比较常见的场景为：目前我们有一个打印字体的训练集，但是我们希望模型能识别手写字体，这时可能需要逐步提升模型，并保存中间结果，最后融合所有模型；

这类办法将模型看作如下的集成分类器

优化目标为所有学习器学习损失总和最小

这一般不是凸优化问题，可能有多个局部最优解，鲁棒性难以保证，参数数量多，梯度形势复杂，通常没有封闭解；梯度下降法的收敛速度难以保障，基分类器的泛化性能和“好而不同”的设计目标难以保障；

Boosting策略

串行训练个体学习器，新增加的个体学习器重点关注错分的样本，逐步提升集成学习系统的泛化性能,在学习目标中增加错分样本的权重,即重赋权(reweighting)

image-20250527190651672

一类前向分步优化的思路是指每一步优化只新增一个学习器

新增基学习器训练中，已经集成的部分保持不变，优化;

从而转变成一种分布优化目标

这是一种类似greedy的策略，待优化的变量明显减少，但是无法保证解为全局最优；

Adaboost

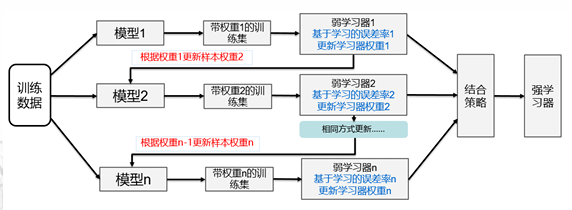
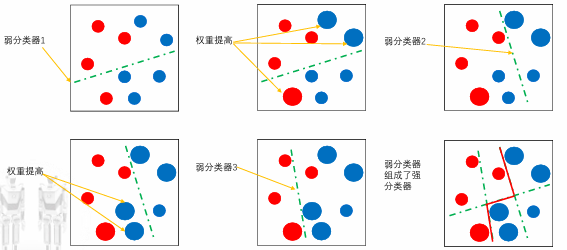
Adaboost(adaptive boosting)自适应增强算法，关注前一个基本分类器分错的样本会得到加强，加权后的全体样本再次被用来训练下一 个基本分类器。同时，在每一轮中加入一个新的弱分类器，直到达到某个预 定的足够小的错误率或达到预先指定的最大迭代次数。

也就是说，后一个模型的训练总是在前一个模型上完成。流程如下

image-20250527192749939

  1. 初始化训练数据的权值分布

    如果有N个样本，则每一个训练样本最开始时都被赋予相同的权值：1/N

  2. 训练弱分类器

    如果某个样本点已经被准确地分类，那么在构造下一个训练集中，它的权值就被降低

    相反，如果某个样本点没有被准确地分类，那么它的权值就得到提高

    权值更新过的样本集被用于训练下一个分类器，整个训练过程如此迭代地进行下去

  3. 将各个训练得到的弱分类器组合成强分类器

    加大分类误差率小的弱分类器的权重，而降低分类误差率大的弱分类器的权重

示意图如下

image-20250527192621290

采用面向二分类问题的加性模型假设,

在分布上任意采样，满足映射;目标优化为最小化指数损失函数

为什么选取这个函数？因为对于梯度为0处求得最优的,到达了贝叶斯最优错误率，说明这个函数是原来分类任务的一致的替代函数。

定义训练数据总量为,维度为,标签为二维的，真实的映射为;

对于时刻的样本分布(训练样本权重向量)

每个个体学习器在分布下的平均误差率为

对于这一类问题，其前向分布优化的过程如下：

将指数损失函数递归式Tylor展开得到

进一步近似得到

求解当前最优的基学习器为

注意到除以某个常数结果不变，记

递归表示如下

于是最优解（注意D下标变化）就是最小化错误分类

考虑前向分步最小化求解

令内式的梯度为0，求解

显然上述推导用到了太多的近似，并非一定是全局最优的，可以按照如下伪代码迭代

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
\usepackage{algorithm, algpseudocode, amsmath}

\begin{algorithm}
\caption{AdaBoost Algorithm}
\label{alg:adaboost}
\begin{algorithmic}[1]
\Require Training Data $X = \{\mathbf{x}_1, \dots, \mathbf{x}_N\}$, Labels $Y = \{y_1, \dots, y_N\}$ where $y_i \in \{-1, 1\}$, Number of Iterations $T$.
\Ensure A strong classifier $H(\mathbf{x})$ represented by a list of base learners and their weights $\{ (h_t, \alpha_t) \}_{t=1}^T$.

\State Initialize sample weights $D_1$: $D_1(i) = \frac{1}{N}$ for $i = 1, \dots, N$.
\State Initialize list of base learners and weights: $\text{Learners} = []$.

\For {$t = 1, \dots, T$}
    \State Train a base learner $h_t$ using a base learning algorithm $\Omega$ on data $(X, Y)$ with weights $D_t$.
    \State Calculate the weighted error rate $\epsilon_t$ of $h_t$:
    $\epsilon_t = \sum_{i=1}^N D_t(i) \cdot \mathbb{I}(h_t(\mathbf{x}_i) \neq y_i)$ \Comment{$\mathbb{I}(\cdot)$ is the indicator function}
    \If {$\epsilon_t > 0.5$ or $\epsilon_t = 0$}
        \State Break loop or handle as edge case.
    \EndIf
    \State Calculate the weight $\alpha_t$ for base learner $h_t$:
    $\alpha_t = \frac{1}{2} \ln\left(\frac{1 - \epsilon_t}{\epsilon_t}\right)$
    \State Add $(h_t, \alpha_t)$ to $\text{Learners}$.
    \State Update sample weights for the next iteration $D_{t+1}$:
    \State Initialize normalization factor $Z_t = 0$.
    \For {$i = 1, \dots, N$}
        \State $D_{t+1}(i) = D_t(i) \exp(-\alpha_t \cdot y_i \cdot h_t(\mathbf{x}_i))$
        \State $Z_t = Z_t + D_{t+1}(i)$
    \EndFor
    \For {$i = 1, \dots, N$}
        \State $D_{t+1}(i) = \frac{D_{t+1}(i)}{Z_t}$ \Comment{Normalize weights}
    \EndFor
\EndFor

\State \textbf{Output:} The strong classifier $H(\mathbf{x})$. For a new sample $\mathbf{x}$, the prediction is given by:
\State $H(\mathbf{x}) = \text{sign}\left(\sum_{t=1}^T \alpha_t h_t(\mathbf{x})\right)$

\end{algorithmic}
\end{algorithm}

image-20250527204548931

该算法对基学习器提出了一定要求，比如CART决策树，神经网络

  • 比较容易将样本权重整合到基学习器的训练过程中
  • 基学习器的表征和泛化能力便于用参数来调节
  • 数据权重扰动对基学习器训练结果影响较大

GBDT算法

GBDT（Gradient Boosting Decision Tree）是一种迭代的决策树算法，该算法由多棵决策树组成，GBDT的核心在于累加所有树的结果作为最终结果，所以 GBDT 中的树都是回归树，不是分类树，它是属于Boosting 策略。GBDT是被公认的泛化能力较强的算法。

对于每一棵决策树的结果可以表示为叶子结点的加权结果

GBDT的预测结果为

前向分步表示为

分类问题损失函数一般选用指数损失函数，回归问题选用平方误差损失，这里就是平方误差；

显然，新到来的决策树就是对先前集成模型的残差拟合

image-20250527213942093

一个更精细的模型算法流程如下：

image-20250527214129208