Convolution Neural Network

Introduction

卷积神经网络是受生物学上感受野(receptive Field)的机制而提出的

在视觉神经系统中，一个神经元的感受野是指视网膜上的特定区域，只有这个区域内的刺激才能够激活该神经元;

感受野机制主要是指听觉、视觉等神经系统中一些 神经元的特性，即神经元只接受其所支配的刺激区域内的信号。

架构

卷积神经网络一般是由卷积层、池化层 和全连接层交叉堆叠而成的前馈神经网络。全连接层一般在卷积网络的最顶层。

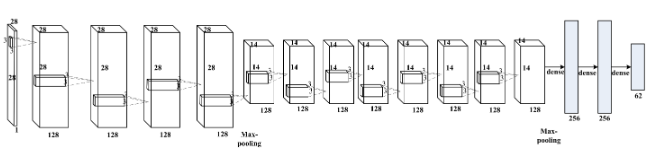
卷积神经网络有三个结构上的特性：局部连接、权重共享以及 池化。这些特性使得卷积神经网络具有一定程度上的平移、缩放和旋转 不变性。和前馈神经网络相比，卷积神经网络的参数少。

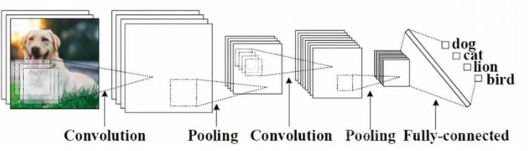
卷积

一维卷积

给定一个输入信号序列和滤波器(filter)/卷积核(convolution kernel)，其卷积输出为

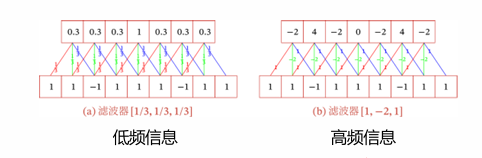
一维卷积常用于信号处理，用于计算信号的累计延迟；

滤波器可以看作信息的衰减率，输出结果为当前时刻产生的信息和以前的延迟信息的叠加；

不同的滤波器可以用来提取序列中的不同特征；定义

• 滑动步长(stride):卷积核在滑动时的时间间隔
• 零填充(Zero Padding);在输入向量两端进行补零

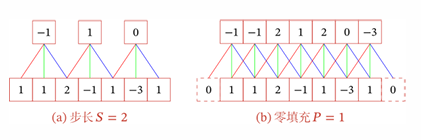
对于大小为的滤波器，根据输出长度的不同可以分为三类

• 窄卷积：步长为1，两端不补零,卷积输出长度为
• 宽卷积：步长，两端补零，卷积后输出长度
• 等宽卷积：步长，两端补零，卷积后输出长度

二维卷积

对于输入图像矩阵,卷积核矩阵,步幅为,卷积结果是一个阶为的方阵;

一般认为,卷积结果具体为

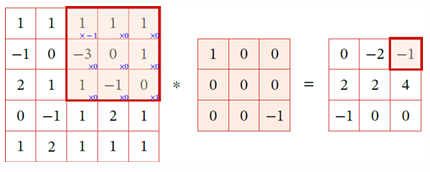
二维卷积有两种不同的方式：通常没有零填充的最优数量处于有效卷积和相同卷积中间的某个位置；

1. 有效卷积：没有padding
2. 相同卷积：输入和输出相同

即是卷积前后图像的宽度，是滤波器的宽度，是零填充的数量，是步长，是卷积前后后图像的高度;

Feature Map

一幅图像在经过卷积操作后得到结果称为特征映射（Feature Map）;


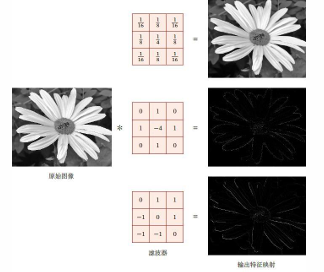
以下是一个图像中的二维卷积的例子：卷积神经网络是针对图像处理设计的特殊的网络结构，在图像处理中，卷积经常作为特征提取的办法，常用的均值滤波就是二维卷积，将当前位置的像素值设置为卷积核内所有像素的平均值；

卷积层

在FFN中，连接边的数量为前后两层神经元个数的乘积，当神经元数量巨大，权重矩阵训练效率较低；卷积运算具有特征抽取的能力，卷积层中每一个神经元都只和下一层某个局部窗口的神经元相连，因此连接边数降至为后一层神经元数量和卷积核大小的乘积；

一个常见的减少连接边的常见trick是权值共享，我们认为同一个卷积核能对应提取一个特征，卷积核对于第层的所有的神经元都是相同的。权重共享可以理解为一个卷积核只捕捉输入数据中的 一种特定的局部特征。因此，如果要提取多种特征就需要使用多个不同的卷积核。

这样的稀疏交互方式，即局部连接或者局部感受野的方式，既能进行特征提取，又加快了计算效率；但是卷积层并没有显著减少特征映射中的神经元个数；

池化层

池化层(Pooling Layer),也即子采样层(subsampling layer)，用于卷积层之后，降低特征维数，减少参数数量，从而避免过拟合；

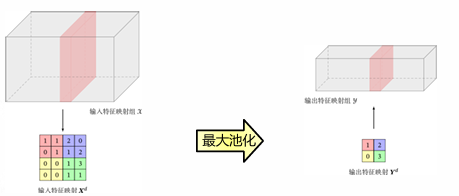
对于池化层的输入图特征映射组为,对于其中每一个特征映射,将它们划分为多个区域(可以重叠也可以不重叠)，池化操作就是对每个区域进行下采样，作为这个区域的概括。

一般分为两种：

• 最大池化(max pooling):对于一个区域，选择该区域的最大活性值的神经元,主要用来抑制邻域值之间差别过大，造成的方差过大。对纹理的提取较好；

• 平均池化(mean pooling):是取区域内所有神经元活性值的平均值,能够抑制网络参数误差造成的估计均值偏移的现象。对背景的保留效果较好；

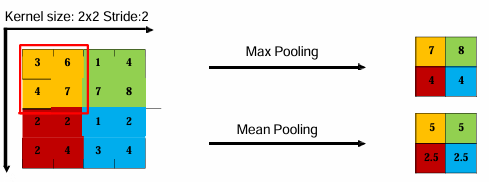
从定义方式我们可以看出来，池化操作可以更高地获取平移不变性，减少了神经元数量，并获得了更高的计算效率；

全连接

图像特征图的“分布式特征表示”映射到样本标记空间。在整个卷积神经网络中起到“分类器”的作用。最后一层的全连接层起到的作用就是输出结果;

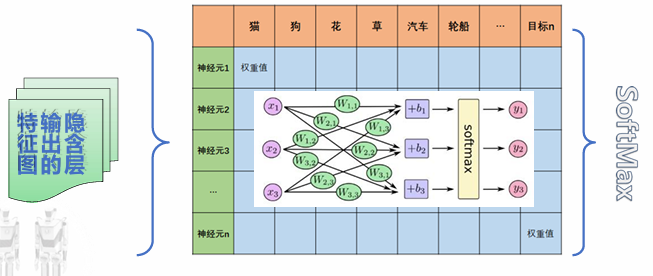
通过Softmax函数将多个标量映射为一个概率分布，输出分类结果的置信度。