Introduction

如果我们相信聚集在一起，有较高相似性的簇一定有有趣的知识的话，那么聚类分析就是获得数据内部结构，发现簇的意义的方法。

在讨论聚类算法时，都是在无监督学习的框架下进行的，也就是已知的数据集是没有标签可以学习的。

聚类：将数据分为多个簇(Clusters)，使得在同一个簇内对象之间具有较高的相似度，而不同簇之间的对象差别较大。

任务

已知无标记样本集 , 聚类的算法的任务就是划分样本集成个互不相交的簇，集 划分为 个不相交的簇：

对样本,应有唯一的下标,使得;

聚类的结果可用包含 个元素的簇标记向量 ​ 表示；

功能

聚类分析是获得数据内部结构的有效方法。通过观察聚类得到的每个簇的特点，可以集中对特定的某些簇作进一步分析。

聚类分析可以作为其它算法的预处理步骤；

聚类分析可以完成噪声点/孤立点的挖掘；

指标

对于聚类任务，我们希望物以类聚，直观上有两个指标：

  • 「簇内相似度（intra-cluster similarity）」高
  • 「簇间相似度(inter-cluster similarity)」低

外部指标

对数据集 ,聚类簇划分 , 参考模型簇划分为 ,令 与 分别表示与 和 对应的簇标记向量.

对样本配对，一定是下面四种情况之一：

显然，

  • Jaccard 系数(Jaccard Coefficient, JC)

  • FMI 指数(Fowlkes and Mallows Index, FMI)

  • Rand指数(Rand Index, RI)

聚类算法的距离度量

四种方式：最小距离，最大距离，中心距离，平均距离

聚类算法的分类

  • 基于原型/划分的办法：K-Means, K-Medoids
  • 基于层次的办法：AGENS, DIANA
  • 基于密度的办法：DBSCAN
  • 基于网络的办法：STING

prototype-based clustering

Idea

基于原型的聚类算法(prototype-based clustering)法假设聚类结构能通过一组原型刻

初始化一个划分，之后通过迭代的办法优化这个划分方式；

如何定义优化？我们需要一个聚类目标函数作为指标：簇对象到簇中心平方误差

Kmeans

对于K-means算法，我们提出一种基于expectation maximization的实现；

损失函数是最小化平方误差

此损失函数刻画了簇内样本围绕簇均值向量的紧密程度，J 值越小，则簇内样本相似度越高；

优化目标是找到使得代价最小化的和向量；

初始均值-簇分配-更新均值-收敛，如下：

Kmeans算法伪代码

一个直观的例子如图所示：

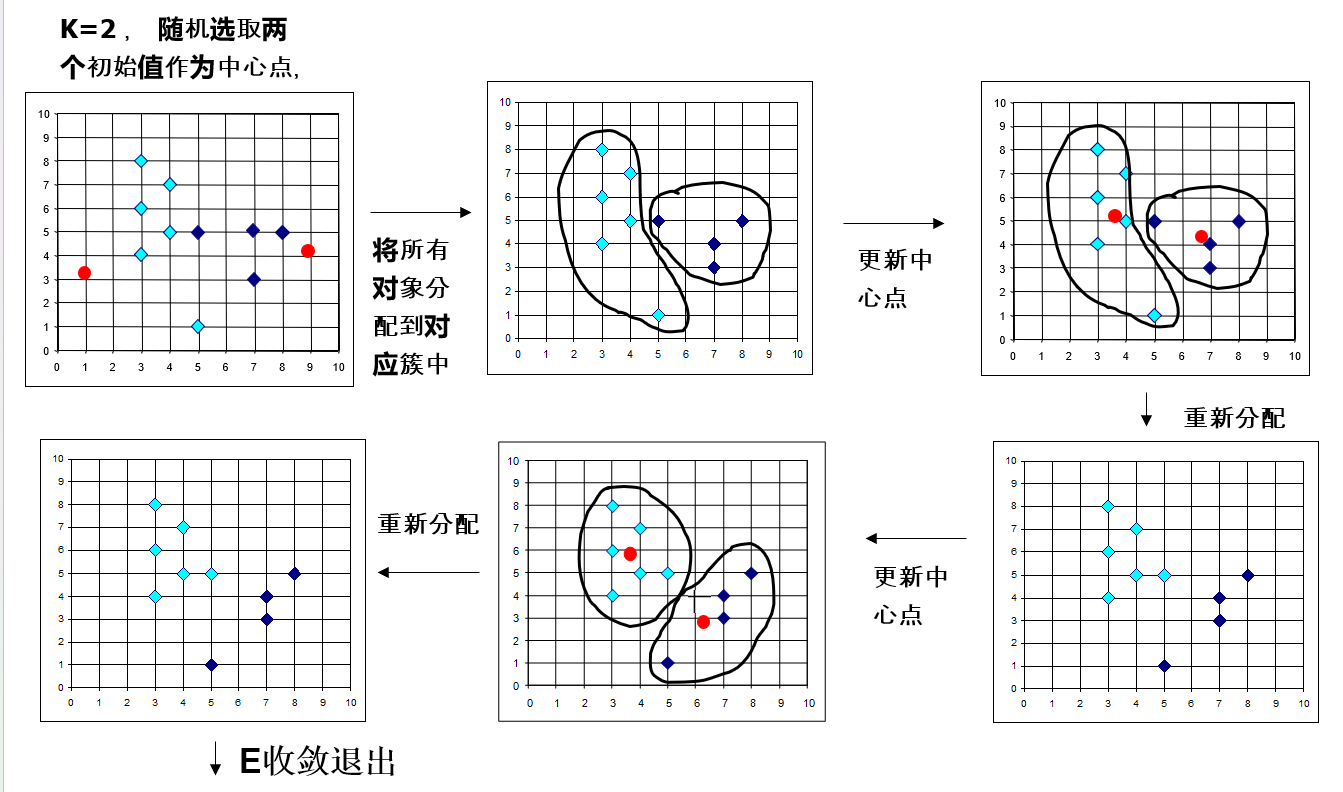
Kmeans算法流程示意图

优点：经典算法，简单、快速， 对处理大数据集，该算法是相对可伸缩和高效率的。

缺点：

  • 初始值敏感；
  • K需要预先设定，不是**Parameter-free **的；
  • 只能发现类球状簇,不适合于发现非球形状的簇或者大小差别很大的簇；
  • 离群点敏感；

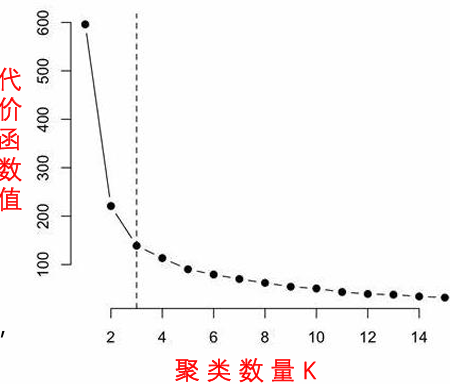
这里K值的选取可以根据肘部法则，我们可能会得到一条类似于人的肘部的曲线。 代价函数的值会迅速下降，在𝐾=3的时候达 到一个肘点。在此之后，代价函数的值会就下降得非常 慢，所以，我们选择𝐾=3；

肘部法则

中心点的选取一般是随机初始化，计算更新为簇内数据的平均向量；通常几轮时间就收敛了；

这里有一个trick： 二分K均值方案，不容易受到初始化问题的影响，类似于一种层次聚类的思想  基本思想，为了得到K个簇，先分为2个簇，然后不断选择其中一个分裂；可以看作一个逐步求精的过程；

Bisecting-K-means

基于高斯混合模型的聚类实现

高斯混合聚类 (Mixture-of-Gaussian, MoG) 是一种基于概率模型的聚类方法。

与 K-Means 等基于距离原型的算法不同，MOG认为观测到的数据集是由 个不同的高斯分布混合生成的。对于数据集中的每一个点，它属于某个特定簇的可能性可以用概率来衡量。

模型假设：假设数据集 是由 个高斯分量混合生成，其概率密度函数为：

其中：

  • 是第 个高斯分量的混合系数（或称先验概率），表示数据点来自第 个簇的概率，满足 且 ;
  • 是第 个高斯分量概率密度，参数为均值向量 和协方差矩阵 ;

目标： 学习这些高斯分量的参数 ，使得这些模型参数能够最大化似然函数,问题在于数据是未标记的，学习是无监督的；

算法： 通常使用EM算法来估计模型的参数。EM 算法是一个迭代过程，包含两个步骤：

  • E 步 (Expectation Step)：估计观察到数据点后，每个高斯分量的后验概率（称为"责任"或"soft assignment"）。对于每个数据点 和每个簇 ，计算其属于簇 的概率 ：

    这步利用当前的模型参数来计算每个点属于每个簇的概率。

  • M 步 (Maximization Step)：利用 E 步计算出的后验概率，重新估计每个高斯分量的参数 ，以最大化加权后的数据点的似然。这步根据每个点对每个簇的"贡献度"（后验概率）来更新簇的参数。

    似然函数为

    更新均值：

    更新协方差：

    更新混合系数:

重复 E 步和 M 步，在算法收敛后，每个数据点 可以被分配到其后验概率 最大的那个簇 。这是一种hard assignment。或者，可以保留其属于各个簇的概率信息(soft assignment)。

优点

  • 概率解释： 提供了每个点属于每个簇的概率，不仅仅是简单的簇分配。
  • 簇形状灵活： 通过协方差矩阵可以建模非球状的簇（K-Means 隐式假设簇是球状且方差相等）。

缺点

  • 参数敏感： 需要预先指定簇的数量 。
  • 局部最优： EM 算法容易陷入局部最优解，结果可能依赖于参数的初始化。
  • 计算成本： 相对于 K-Means，计算成本更高，特别是对于大数据集或高维数据。
  • 假设前提： 假设数据是由高斯分布生成的，如果数据分布与高斯分布差异较大，效果可能不好。
  • 对噪声和离群点敏感： 离群点可能会对均值和协方差的估计产生较大影响。

算法流程伪代码如下：

image-20250528131033659

基于层次的办法

层次聚类方法对给定的数据集进行层次的分解，直到某种条件满足为止。

凝聚的层次聚类：

  • 一种自底向上的策略，首先将每个对象作为一个簇，然后合并这些原子簇为越来越大的簇，直到某个终结条件被满足，
  • 代表是AGNES算法

image-20240528020729807

最小距离法（Single Linkage）

  • 定义：在两个簇之间的所有可能配对样本点中，选择距离最小的一对样本点的距离作为簇间距离。

  • 链状效应：由于只考虑最接近的一对点，最小距离法容易形成链状结构，即若干个样本逐个连接在一起，形成较长的"链"。

  • 噪声敏感：对噪声和离群点（outliers）较为敏感，因为离群点可能会导致簇之间的最小距离变小，从而错误地合并簇。

  • 效率较高：计算简单，效率较高，但结果可能不稳定。

  • 适用场景：适用于数据集中的簇呈现不规则形状或链状结构的情况。

最大距离法（Complete Linkage）

  • 定义：在两个簇之间的所有可能配对样本点中，选择距离最大的一对样本点的距离作为簇间距离。
  • 紧密簇：最大距离法倾向于形成紧密、球形的簇，因为它考虑了簇中最远样本点之间的距离，从而避免形成链状结构。
  • 抗噪声能力强：对噪声和离群点较为鲁棒，不容易被离群点影响，因为离群点的存在不会显著改变簇的最大距离。
  • 计算复杂度高：由于需要计算所有样本点的最大距离，计算复杂度相对较高。
  • 适用场景：适用于数据集中簇的形状较为规则、且希望得到更紧密的簇的情况。

分裂的层次聚类：

  • 采用自顶向下的策略，它首先将所有对象置于一个簇中，然后逐渐细分为越来越小的簇，直到达到了某个终结条件。

  • 代表是DIANA算法;

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    算法    DIANA（自顶向下分裂算法）
    输入：包含n个对象的数据库，终止条件簇的数目k。
    输出：k个簇，达到终止条件规定簇数目。
    （1）将所有对象整个当成一个初始簇；
    （2） FOR (i=1; i≠k; i++) DO BEGIN
    （3）       在所有簇中挑出具有最大直径的簇C；
    （4）      找出C中与其它点平均相异度最大的一个点p并把p放入splinter group，剩余的放在old party中；
    （5）.      REPEAT
    （6）             在old party里找出到最近的splinter group中的点的距离不大于到old party中最近点的距离的点，并将该点加入splinter group。
    （7）       UNTIL 没有新的old party的点被分配给splinter group；
    （8）   splinter group和old party为被选中的簇分裂成的两个簇，与其它簇一起组成新的簇集合。
    （9） END.

基于密度的聚类算法：DBSCAN

只要一个区域中的点的密度大于某个阈值，就把它加到与之相近的聚类中去。

对于一个类中的每个对象，在其给定半径的领域中包含的对象不能少于某一给定的最小数目；

概念：

设置半径阈值,数量阈值;

核心对象的-邻域至少包个对象；

从核心对象出发，对任何邻域内的点直接密度可达；

如果存在一个对象链，，，，，，对，，是从关于直接密度可达的，则对象是从对象相互密度可达的。

如果存在一个对象，使得对象和是从关于密度可达的，那么对象和是密度相连的。

一个基于密度的簇是基于密度可达性的最大的密度相连对象的集合 ;

  • 连接性：密度相连；
  • 最大性：由密度可达，

DBSCAN算法先任选数据集中的一个核心对象为"种子" ,再由此出发确定相应的聚类簇;

算法类似于BFS搜索，维护一个队列；

image-20240528023600204

优点：

  • 能克服基于距离的算法只能发现"类圆形"的聚类的缺点，可发现任意形状的聚类；
  • 对噪声数据不敏感；

缺点：

  • 计算复杂度大，需要建立空间索引来降低计算量；
  • 数据维数的伸缩性较差；
  • 对参数非常敏感；
  • 如果数据库比较大的时候要进行大量的I/O 开销;
  • 很难找到不同密度的簇;

基于网格的聚类：STING

基本思想：将对象空间量化为有限数目的单元，形成一个网格结构，所有的聚类都在这个网格结构中上进行。

其优点是处理速度很快，其处理时间独立于数据对象的数目，只与量化空间中每一维的单元数目有关。

在网格聚类方法中有利用存储在网格单元中的统计信息进行聚类的STING算法和在高维数据空间基于网格和密度的聚类方法等。

STING是一种基于网格的多分辨率聚类技术，它将空间区域划分为矩形单元。针对不同级别的分辨率，通常存在多个级别的矩形单元，这些单元形成了一个层次结构：高层的每个单元被划分为多个低一层的单元。高层单元的统计参数可以很容易的从底层单元的计算得到。这些参数包括属性无关的参数count、属性相关的参数m（平均值）、s(标准偏差)、min(最小值)、max(最大值)以及该单元中属性值遵循的分布类型。

STING算法采用了一种多分辨率的方法来较粗，则聚类质量会受到影响。进行聚类分析，该聚类算法的质量取决于网格结构最低层的粒度。如果粒度比较细，处理的代价会显著增加；

STING算法的主要优点是效率高，通过对数据集的一次扫描来计算单元的统计信息，因此产生聚类的时间复杂度是O(n)。在建立层次结构以后，查询的时间复杂度是O(g), g远小于n。STING算法采用网格结构，有利于并行处理和增量更新。