有限自动机

形式定义

在词法分析中，有限自动机 (Finite Automata, FA) 是识别词素模式的核心理论基础。 有限自动机可以非常高效地处理输入字符流，判断它们是否符合某个模式，比如正则语言 (Regular Languages)。

对于一个有限自动机(FA),定义如下：

  • 字符集 :规定自动机输入的字符范围；
  • 状态集合 :DFA有向图上的顶点；
  • 唯一起始状态 : ,为自动机的起点，转移到其他状态；
  • 接受状态集合 : 满足 ;
  • 转移函数 : 输入为当前状态和读入字符，输出为下一步状态，为DFA有向图的边；

定义自动机,若其能识别字符串,则，否则为不接受/识别；

一个NFA接受字符串，当且仅当对应的转换图存在一条从开始状态到某个接受状态的路径，路径上的标号组成该字符串；

若状态不存在对字符的转移，定义为 ,也代指无法转移中任何一个状态；

正则语言

不确定的有限自动机(NFA)对边上的标号没有任何限制，一个符号标记离开同一状态的多条边，并且空串也可以当作标号；

确定有限自动机(DFA)对每个状态和字母表的每个符号，DFA有且仅有一条离开该状态，以该符号为标号的边；

DFA和NFA能识别的语言集合是相同的，也正好是能用正则表达式描述的语言的集合，我们统称为正则语言(regular language);

子集构造技术

我们可以尝试将DFA或者NFA表示为一张转换图

  • 结点表示状态；
  • 带标号的边表示自动机的转换函数；同一个符号可以标记同一状态出发到达多个目标状态的多条边，一条边的标号可以是字母表的符号或者空串；

对于正则表达式(a|b)*abb，下图给出了NFA示意图和对应的状态转换表；

image-20250530143432186

image-20250530143510721

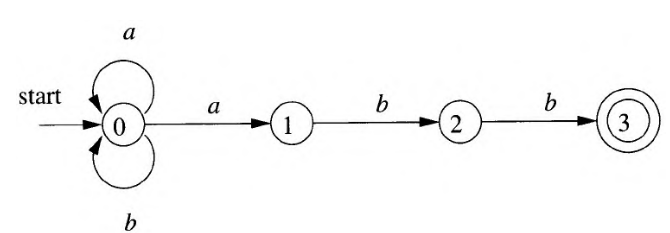
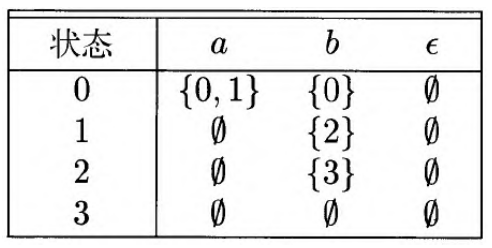
DFA相较于NFA，具有如下特性，区别在于转换函数：

  • 没有输入空串的转换动作；
  • 对于每个状态和每个输入符号，有且仅有一条标号的边离开;

下图给出了正则表达式(a|b)*abb对应的DFA；

image-20250530144023800

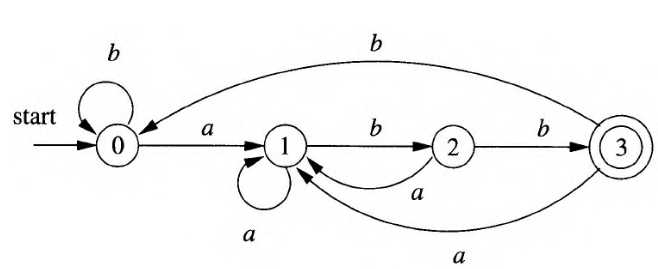
我们可以通过子集构造(subset construction)技术，实现从NFA到DFA的转换；

对于输入的NFA，定义三类操作

  • closure(T)：找到状态集合通过NFA中不经过有意义的符号转换可以到达的状态集合；显然;
  • move(T,a)：找到T中某个状态s出发通过标号a的转换可以到达的NFA状态集合；

image-20250530150300491

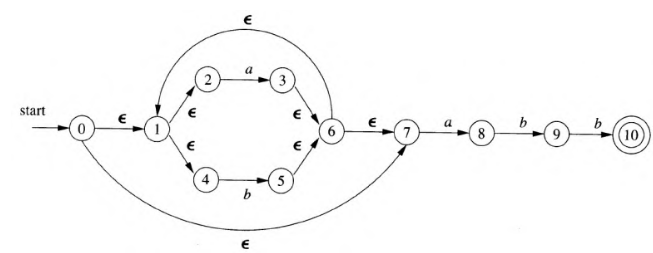
在上图的例子中，MOVE({0,1,2,4,7}, a)={3, 8};MOVE({6},ε) = {1,7};closure({0}) = {0,1,7,2,4}; closure({6})={6,1,7,2,4},closure({3,8})={3,8,6,1,7,2,4};

计算closure的算法如下：

image-20250530152230642

算法流程如下：

输入：NFA可表示为;

输出：等价的DFA，表示为

  • ，起初只有一个元素,，且未加标记；
  • 两个FA的字符表相同；
  • ;

过程如下图：

image-20250530152002383

值得注意的是，该算法维护了一张表格Dtran；

image-20250530152355689

最后输出的DFA如下图：

image-20250530152558337

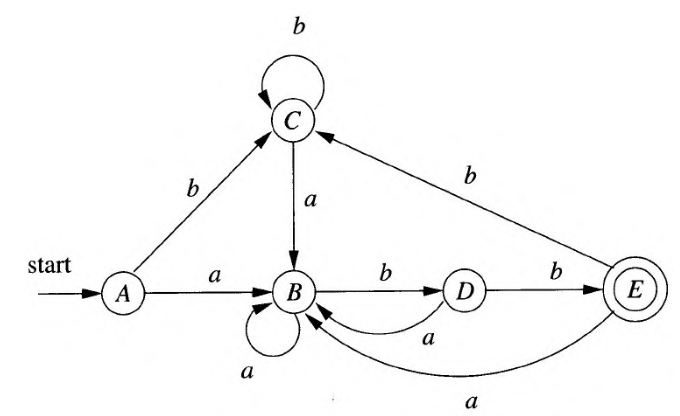
DFA构造

自动机在词法分析中的工作流程: 🚶➡️🪙

  1. 定义模式: 使用正则表达式为每种记号类型（如标识符、数字、关键字、操作符）定义模式。
  2. 构造自动机:
    • 为每个正则表达式构造一个 NFA。
    • 将所有 NFA 合并为一个大的 NFA（通过引入新的起始状态和到各个 NFA 起始状态的 ε-转移）。
    • 将合并后的 NFA 转换为一个 DFA (例如，使用子集构造法)。
    • （可选但推荐）最小化该 DFA,指消除死状态；

image-20250530152811312

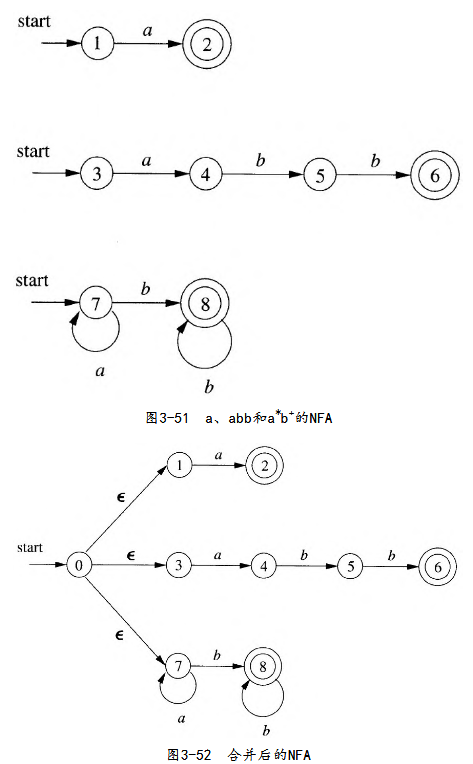
DFA运行

  1. 词法分析器从 DFA 的起始状态开始。

  2. 逐个读取输入字符流中的字符。

  3. 根据当前状态和输入字符，DFA 转换到下一个状态。

  4. 如果 DFA 到达一个**接受状态 **，这意味着已经识别出一个与该接受状态关联的模式的词素。

    最长匹配原则 (Longest Match Principle): 如果输入串的多个前缀都能匹配一个或多个模式，词法分析器会选择匹配最长可能词素的那个。

    例如，如果 if 是关键字，iffy 是标识符，输入 iffy 时，会匹配 iffy 而不是 if。

  5. 如果 DFA 在某个点无法进行有效转换（即卡在某个非接受状态，且没有对应当前输入字符的转移），或者输入结束但未处于接受状态，则可能发生词法错误。