Uninformed Search

Posted on

假设下面搜索问题按照下图举例：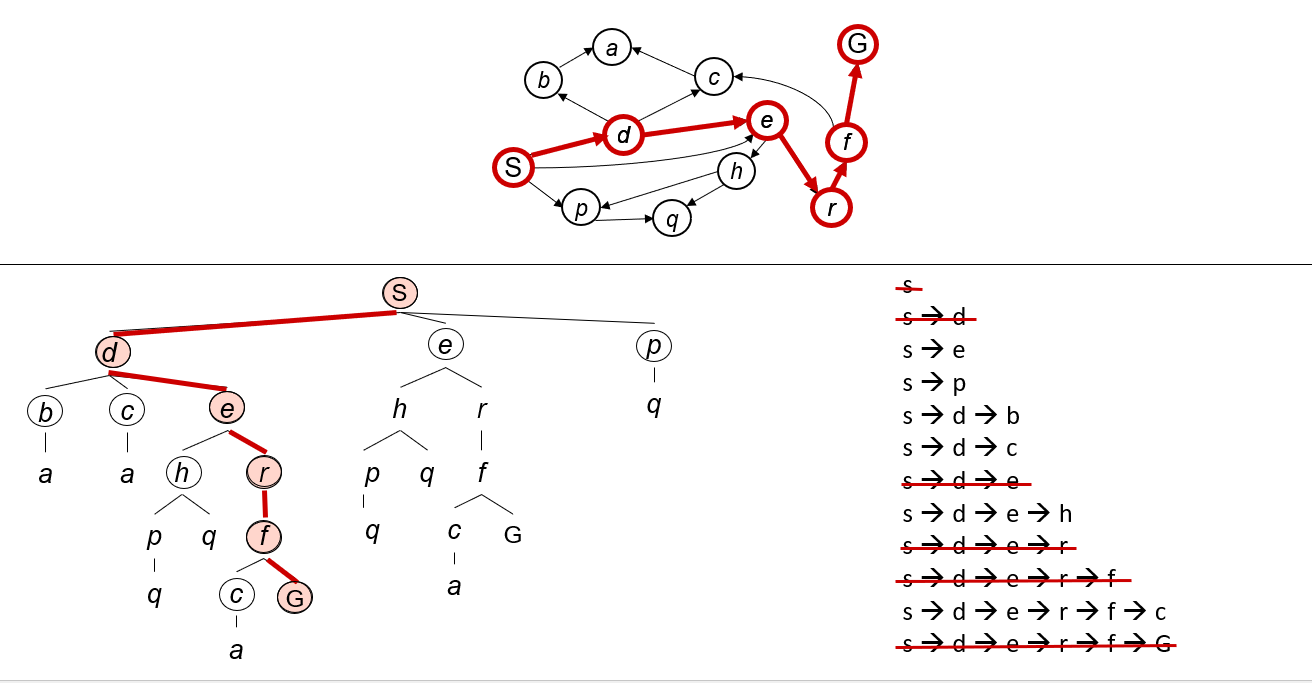
image-20240612180603977

DFS总是拓展搜索树中当前边缘节点集中的最深的结点，很快搜索推进到没有后继的最深层，将它们从边缘节点集去掉后，回溯到下一个稍浅的未拓展后继的结点；

做到这一点的关键是维护一个栈，每次保证当前看到最深的结点在栈顶，优先弹出的也是已经被搜完的栈顶结点；

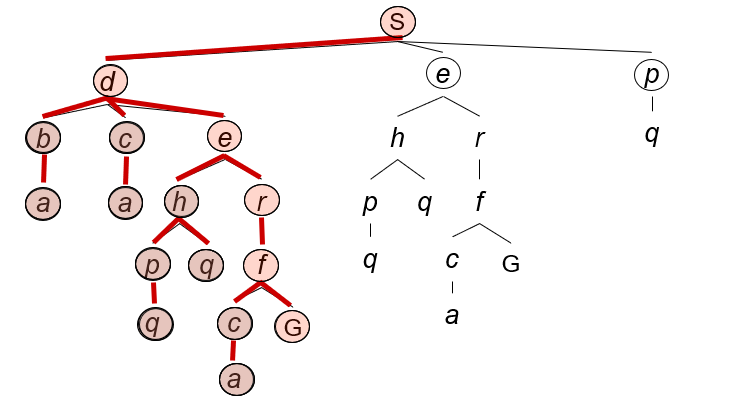
image-20240612180510158

我们从四个性能度量考察DFS：

  • 完备性：
    • 在避免了重复状态和冗余路径，优先状态空间中图搜索完备；
    • 但是对于树搜索可能会陷入死循环，不过可以优化检查根节点到当前结点的新节点，但还是无法避免冗余路径；
    • 遭遇无限且无法到达目标结点的路径则会失败；
  • 最优性：优先左子树可能会导致路径变长，代价变大，错过最优解，尽管到达了目标结点；
  • 时间复杂度：若搜索一致树每个状态有$b$个后继，对于$m$为任意结点的最大深度，$d$为最浅解的深度，DFS可能会在搜索树上生成所有$O(b+b^2+\cdots+b^m)=O(b^m)$个结点；
  • 空间复杂度：只需要存储根节点到叶节点的路径可以做到$O(bm)$，具有很大优势；

BFS总是拓展深度最浅的结点，直到目标检测被通过。这意味着浅层的结点会在深层结点来临之前被拓展，这通过队列(Queue)很容易实现；

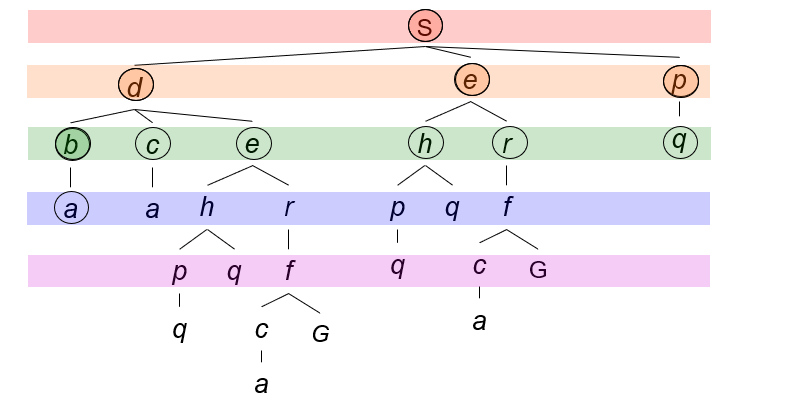
image-20240612180444111

我们从四个方面考察BFS的性能：

  • 完备性：若通过结点通过目标检测，那么一定是最浅结点，因为更浅的结点没有通过目标检测；因此BFS是完备的；
  • 最优性：若路径代价是基于深度的非减函数，那么BFS是最优的；
  • 时间复杂度：最坏情况下目标为最后一层结点，解的深度为$d$,目标检测在选择拓展结点时，时间复杂度为$O(b^{d+1})$;
  • 空间复杂度：已拓展的每个结点都保存在探索集中，因此空间复杂度为$O(b^d)$,几乎不能忍受；

UCS总是拓展代价最小的结点，直到需要将边缘结点集组织成按代价排序的优先队列来实现；

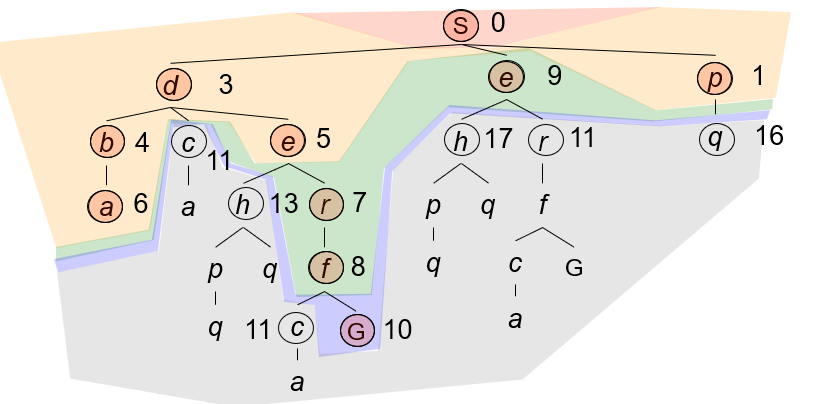
image-20240612180420901

下面从四个方面考察UCS的性能：

  • 完备性：UCS对解路径的步数并不关心，因此若存在零代价的行动，那么UCS可能会陷入死循环，否则代价都是正直的话，UCS是完备的；
  • 最优性：目标检测发生于结点被拓展时进行，而不是在生成时进行，第一个生成的目标结点可能在次优路径上，也就是说目标结点被搜索到时并不会立即停止算法，而是等待可能到目标结点的路径都被（部分，因为代价过大的路径可能就不会搜了）探索过后，比较最小的代价后再返回；
  • 时间复杂度：假设最优解代价为$c$,单步行动最小代价为$\varepsilon$,那么最坏时间复杂度为$O(b^{1+[\frac c\varepsilon]})$,因为在探索代价大的行动前，会先探索代价小的行动所在的搜索树；
  • 空间复杂度：同$O(b^{1+[\frac c\varepsilon]})$

为了避免无限循环的DFS失败，对DFS设置探索界限$l$，深度为$l$​的结点被视作没有后继；

选择一个好的$l$值往往是困难的，对于大多数问题，如果它没被解决，是无法知道一个好的深度界限的；

我们从四个方面考察DLS的性能：

  • 完备性：设置$l<d$,DLS无法搜到目标节点，也就是不完备的；
  • 最优性：设置$l>d$,同DFS一样不是最优的；
  • 时间复杂度：被剪枝为$O(b^l)$;
  • 空间复杂度：$O(bl)$;

结合DFS和BFS的优势，它经常和深度优先搜索结合使用确定更好的深度界限；

初始化深度限制$l=0$,不断增大它，直到找到目标，当$l=d$的时候，即最浅的目标节点所在深度时，就能找到；

我们从四个方面考察IDS的性能：

  • 完备性：同BFS，分支因子有限时搜索算法完备；
  • 最优性：同BFS，代价函数为结点深度的非减函数时最优；
  • 时间复杂度：上层结点被重复生成，存在解时时间复杂度为$O(db+(d-1)b^2+\cdots+b^d)=O(b^d)$;
  • 空间复杂度：同$O(bd)$;

并不是每一个问题都能运用双向搜索，比如8皇后问题，但是对于一个使用BFS的搜索问题，解的深度为$d$意味着时间复杂度为$O(b^d)$,但是同时对起始和目标同时BFS直到相遇看起来时间复杂度为$O(2b^{d/2})$,这要小得多；

Search and Models

Search operates over models of the world

  1. The agent doesn’t actually try all the plans out in the real world;
  2. Planning is all “in simulation”
  3. Your search is only as good as your models…