Background
和动画实验一样,这次也是用matlab和python共同实现,完成对Taylor中值定理,Euler公式,Fourier公式的验证;
这次我们需要的python库:sympy,这个库能让我们像matlab一样完成符号运算;
Content
Taylor公式
先给出Taylor中值定理:
若$f(x)$在$x_0$的临域$U(x_0)$具有直到$n+1$阶导数,则当在$(a,b)$内,$f(x)$可以表示为关于$x-x_0$的$n$次多项式$P(x)$与一个余项$R_n(x)$之和:
$$
f(x)=P(x)+R_n(x)=\sum_{k=0}^{n}\frac{f^{k}(x_0)}{k!}(x-x_0)^k+R_n(x)
$$
$$
R(n)=\frac{f^{n+1}(\epsilon)}{(n+1)!}(x-x_0)^{n+1},\epsilon \text{在}x_0,x\text{之间}
$$
在matlab中利用taylor函数可以直接求出对应展开阶数的P(x),taylor函数的接口如下:
T = taylor(f,var,a)
f是即将展开的函数;
var指定要展开的自变量;
a指定拓展点,也就是说T展开应该是关于(x-a)的多项式;
T = taylor(___,Name,Value)
Name和Value是在此之上的选项,例如,可以指定泰勒级数的扩展点、截断顺序或顺序模式扩张。
'ExpansionPoint',x0,指定拓展点为x0
order,n指定展开阶数
下面是对$sin(x)=x-\frac{x^3}{6}+…+(-1)^{\frac{n-1}{2}}\frac{x^n}{n!}+o(x^n)$的展开实验代码
matlab:
1 | syms x |
通过matlab拟合出来的图像是这样的:
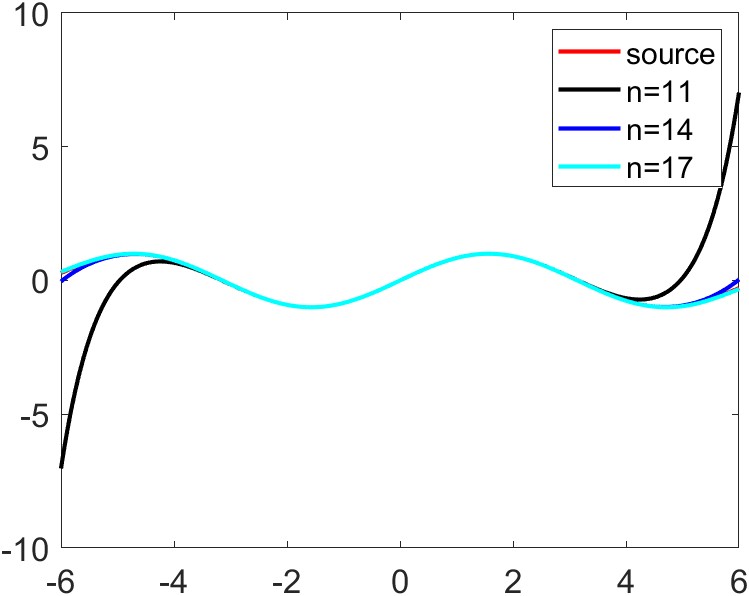
python:
这里需要注意的小点是:利用sympy中的series方法得到的talor展开是带$O(x^N)$的符号式,记得需要用removeO方法去掉,同时将sympy的公式用lambdify转化成numpy的公式才能对linspace计算函数值;
在sympy中series方法的接口如下:
expr.series() 方法来对表达式进行级数展开。下面是一些参数:
x: 展开的变量。
x0: (可选)展开点,默认为$ 0$,也就是在 $x=0$ 处展开。
n: (可选)展开式的阶数,就是说要展开到$x-x_0$的几次方。
dir: (可选)展开方向,+ 表示正方向,- 表示负方向(对劳伦展开有用)。
1 | import numpy as np |
最后拟合出来的效果是这样的:
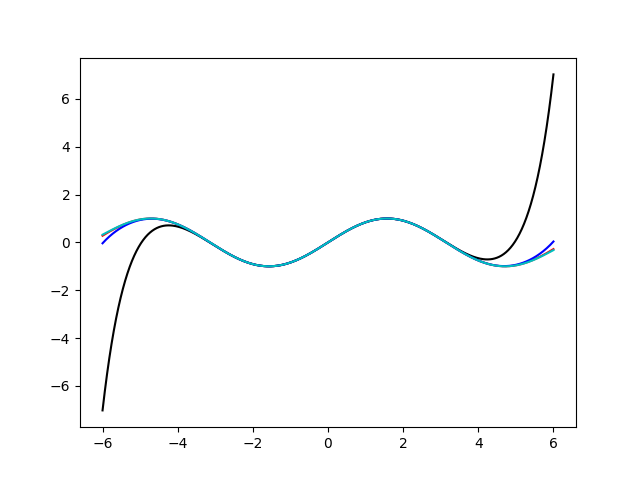
Euler公式
有了Taylor展开的基础后,我们顺便验证Euler公式:$e^{i\theta}=cos\theta + isin\theta$,使用numpy中的复数,对$(-\pi,\pi)$中一系列点,计算两边值是否相等即可;
1 | import numpy as np |
展开的结果确实是
1 | I*sin(z) + cos(z) |
注意Euler公式有一个常见的变形:
$$
cos\ x=\frac{e^{ix}+e^{-ix}}{2},sin\ x= \frac{e^{ix}-e^{-ix}}{2i}
$$
Fourier变换相关
和Fourier变换有许多知识点,比如作者还打算复习之前学过的快速Fourier变换算法,这是一个十分优秀高效的算法,不过在这里只介绍Fourier变换的强大之处,也就是几乎对各种各样的函数的拟合;
注意之前的Taylor展开对函数的拟合其实并不是那么好,基本只能在展开点附近才有比较好的效果,并且Taylor展开本身对函数要求也很高:要求函数在该点具有足够高阶的导数,我们知道许多函数的性质都不是这么好;
先来复习一下Frourier变换
连续函数的正交:
若定义在$(a,b)$函数$f(x),g(x)$满足$\int_{a}^{b}f(x)g(x)=0$则称两函数$f(x),g(x)$在$(a,b)$正交;
如果把函数理解成一系列很密集的散点,那么这些散点构成的向量就满足向量正交的概念,不过在函数取密集的散点向量,不一定是正交的,因为函数描述的是连续的性质,不过我们在工程中经常采用这种近似
关键的积分关系:
- $\int_{-\pi}^{\pi} 1\cdot cos\ nx dx=0(n=1,2,3…)$
- $\int_{-\pi}^{\pi} 1\cdot sin\ nx dx=0(n=1,2,3…)$
- $\int_{-\pi}^{\pi} sin\ kx\cdot cos\ nx dx=0(k=1,2,3…,n=1,2,3…)$
- $\int_{-\pi}^{\pi} cos\ kx\cdot cos\ nx dx=0(k=1,2,3…,n=1,2,3…,k\neq n)$
- $\int_{-\pi}^{\pi} sin\ kx\cdot sin\ nx dx=0(k=1,2,3…,n=1,2,3…,k\neq n)$
- $\int_{-\pi}^{\pi} 1dx =2\pi$
- $\int_{-\pi}^{\pi} sin^2\ kxdx=\pi(k=1,2,3…)$
- $\int_{-\pi}^{\pi} cos^2\ nxdx=\pi(n=1,2,3…)$
$1,cosx,sinx,cos2x,sin2x…$是一串两两正交的函数列
根据工程实践猜想傅里叶级数公式:
若周期信号$f(x)$周期为$T$,角频率为$\omega = \frac{2\pi}{T}$,满足Dirichlet条件:
- 一个周期内只有有限个第一类间断点
- 一个周期内只有有限个极值点
则可以展开成下列级数:
$$
f(x)=\frac{a_0}{2}+\sum_{n=1}^{\infty}a_ncos\ n\omega x+b_nsin\ n\omega x
$$
根据上述「关键的积分关系」待定系数求得:直流分量:$\frac{a_0}{2}=\frac{1}{T}\int_{-T/2}^{T/2}f(x)dx$
傅里叶系数:$a_n=\frac{2}{T}\int_{-T/2}^{T/2}{f(x)cos(n\omega x)dx},b_n=\frac{2}{T}\int_{-T/2}^{T/2}{f(x)sin(n\omega x)dx}$
Fourier级数指数形式:
$f(x)=\sum_{n=0}^{\infty}a_ncos(n\omega x)+b_nsin(n\omega x)=\sum_{n=0}^{\infty}a_n\frac{e^{in\omega x}+e^{-in\omega x}}{2}+b_n\frac{e^{in\omega x}-e^{-in\omega x}}{2i}$
$=\sum_{n=0}^{\infty}e^{in\omega x}\frac{a_n-ib_n}{2}+e^{-in\omega x}\frac{a_n+ib_n}{2}$$=\sum_{n=0}^{\infty}e^{in\omega x}\frac{\frac{2}{T}\int_{-T/2}^{T/2}{f(x)\frac{e^{in\omega x}+e^{-in\omega x}}{2}dx}-i\frac{2}{T}\int_{-T/2}^{T/2}{f(x)\frac{e^{in\omega x}-e^{-in\omega x}}{2i}dx}}{2}+ e^{-in\omega x}\frac{\frac{2}{T}\int_{-T/2}^{T/2}{f(x)\frac{e^{in\omega x}+e^{-in\omega x}}{2}dx}+i\frac{2}{T}\int_{-T/2}^{T/2}{f(x)\frac{e^{in\omega x}-e^{-in\omega x}}{2i}dx}}{2}$
$=\sum_{n=-\infty}^{\infty}F_ne^{in\omega x}$
其中$F_n=\frac{1}{T}\int_{-T/2}^{T/2}f(x)e^{-in\omega x}dx$
将周期信号$f(t)$推广成有限时间的非周期信号,也即时域从周期转化为非周期时,频域从离散的转化为连续的:原始的Fourier变换(FT)
$$
F(\omega)=\int_{-\infty}^{\infty}f(t)e^{-i\omega x}dx
$$$$
f(x)=\frac{1}{2\pi}\int_{-\infty}^{\infty}F(\omega)e^{i\omega x}d\omega
$$离散时间无限频谱内的Fourier变换(DTFT)
将连续信号$f(x)$采样,采样时间点间隔为$T_s$,冲击序列为$\delta_s(x)=\sum_{n=-\infty}^{\infty}\delta(x-nT_s)$,取样信号为$f_s(x)=\sum_{n=-\infty}^{\infty}f(x)\delta(x-nT_s)$,其频谱密度为$F_s(\omega)=\int_{-\infty}^{\infty}f_s(x)e^{-i\omega x}dx=\sum_{n=-\infty}^{\infty}\int_{-\infty}^{\infty}f(x)\delta(x-nT_s)e^{-i\omega x}dx$
$=\sum_{n=-\infty}^{\infty}f(nT_s)e^{-i\omega nT_s}$
离散傅里叶变换(DFT):
对于数组$f[n](0\le n<N)$,定义$f$由离散傅里叶变换得到$F$,
$$
f\xrightarrow[]{DFT}F:F[k]=\sum_{n=0}^{N-1}f(n)e^{-i\frac{2\pi}{N}n\cdot k},k=0,1,…N-1
$$
可待定系数证明$F$由离散傅里叶逆变换得到$f$,
$$
F\xrightarrow[]{IDFT}f:f[n]=\sum_{k=0}^{N-1}F[k]e^{i\frac{2\pi}{N}k\cdot n},n=0,1,…N-1
$$由于暂时没看懂其中的物理意义所以留个坑,貌似这样的式子都是天才一眼看出来的🤣,同时给FFT埋个坑
经过简单的对Fourier变换的复习之后,我们来看看我们的任务:
给以$2\pi$为周期的周期函数$f(x)$在区间定义如下,验证傅里叶级数对其近似效果:
$$
f(x)=\begin{cases}
x^2&-\pi\le x<0\
0&0\le x<\pi
\end{cases}
$$
先看matlab代码
1 | T=2*pi; |
最后拟合出来的效果是这样的,可以看到随着展开阶数增大,拟合效果越来越好,但也可以看到吉布斯现象也越来越显著;
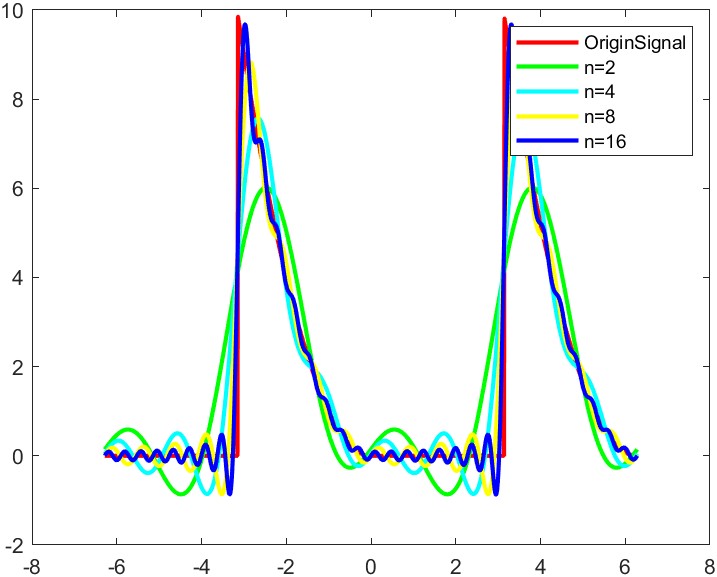
用python也可以做到同样的效果,很遗憾python库里也没有直接计算傅里叶级数的函数;
1 | import numpy as np |
Reamrk
留坑:
- 快速傅里叶变换(FFT)和Cooley-Tukey 算法
- 二维傅里叶变换
- python画CG