Constraint Satisfaction Problems

Posted on

CSP问题

对于CSP问题的形式化描述如下:

  • 变量$X={X_1,X_2,\cdots, X_n}$
  • 值域$D={D_1,D_2,\cdots, D_n}$:每个变量都有自己的值域；
  • 约束集$C$描述变量的取值:有一个变量元组和一个显式的关系函数式描述，例如$<(X_1,X_2),X_1\neq X_2>$
  • 状态有部分或者全部变量的赋值来描述：${X_1=x_1,\cdots,X_n=x_n}$
    • 一个合法的赋值不违反任何约束条件；
    • 一个完整的赋值意味着对每个变量都有赋值；
  • CSP问题的解式全体合法的，完整的赋值的状态

地图着色问题

四色定理就是一类地图着色问题，也是经典的CSP问题：每一个地图（三连通的简单平面图）都是四面可染色的，也即对任意三正则地图$G$均有$\chi’(G)=3$;

对于Australian Map，CSP形式化如下：

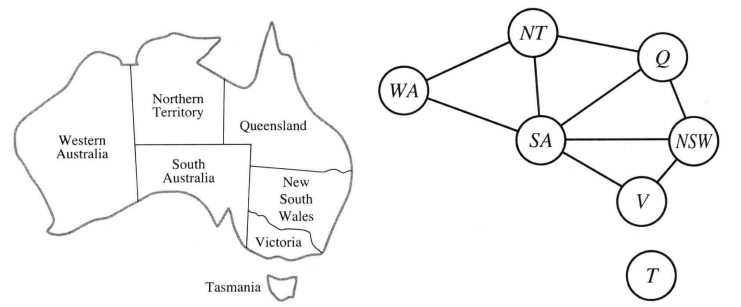
image-20240613200123487

  • $X={WA,NT,Q,NSW,V,SA,T}$
  • $D_i={red,green,blue}$
  • $C={SA\neq WA,SA\neq NT,…, NSW\neq V}$
  • 一个可行的解为${WA=red, NT=green, Q=red, NSW=green,V=red,SA=blu,T=red}$

Varieties of CSPs

对于CSP问题，可以根据变量类型和值域类型进行分类：

  1. 离散变量

    • 有限值域：size $d$ means $O(d^n)$ for complete assignment

      著名的有SAT问题，这是个NPC问题；

    • 无限值域：例如Job scheduling

  2. 连续变量

    • 例如：start/end times for hubble telescope observations

类似于DFS，回溯搜素算法式解决CSP问题的基础的无信息算法，可以描述如下：

  1. One variable at a time：因为CSP问题都是可交换的，就像[WA = red then NT = green] same as [NT = green then WA = red]，因此在每一步只需要考虑一个变量；
  2. Check constraints as you go：固定下一个变量之前，检查约束条件，使得已固定的变量不会相互冲突；

以下是Australian Map的一棵搜索树：

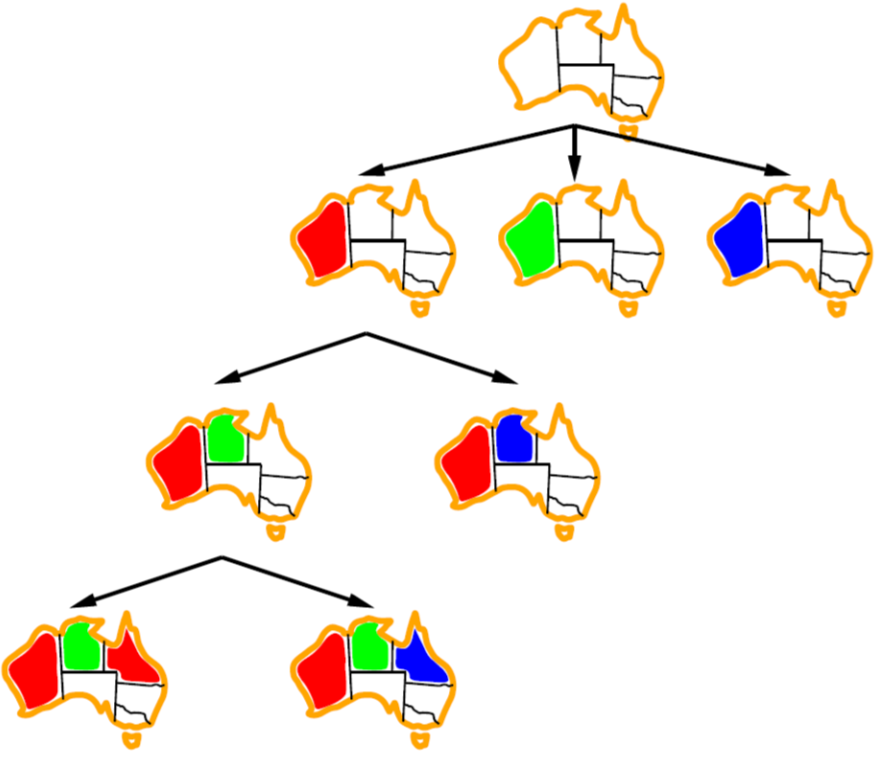
image-20240614012641532

以下是算法伪代码：

image-20240614012845973

简单来说，Backtracking = DFS + variable-ordering + fail-on-violation；

Forward Checking

Filtering

Ordering