计算机组成与结构

Posted on

计算机组成原理

第一章：计算机系统概述

冯诺依曼结构

  • 存储器(MU) :存储指令和数据；
  • 输入单元（IU）：接收输入信号；
  • 输出单元（OU）：发送输出信号；
  • 算数逻辑单元（ALU）：执行算数逻辑操作；
  • 控制单元（CU）：产生各部件的控制信号；

CPU

  • 封装了CU，ALU与寄存器；
  • 通过控制总线、地址总线和数据总线进行互联；
  • 寄存器位于CPU内部，保持和CU、ALU同频，因而速度快于外部存储器；

存储器

  • 随机访问寄存器（RAM）：易失性寄存器，访问速度较快但断电内容消失；
  • 只读寄存器（ROM）：非易失性寄存器，常用于初始化启动指令；
  • 采用“Cache-主存-磁盘”的三级存储结构；

I/O接口与总线

与外界进行信息交互；

计算机性能初步

  • CPU时间不包括程序输入输出时间或者运行其他程序的时间，表示程序在CPU上执行的时间（小于程序的响应时间）；

  • 缩短程序的响应时间能增加吞吐率，反之不一定（可以增加处理器的个数）；

  • CPU使用晶振产生的时钟信号来驱动或者定时；

  • CPU时间=程序时钟周期时间$\times$周期数

    周期数=对应指令集花费的周期数
    $CPU(Pro)=\sum_{A\in Pro}{CPI(A)\times num(A)}$

  • 性能比表示两个计算机的性能差异；

​ $\frac{性能_Ａ}{性能_B}= \frac{CPU(B)}{CPU(A)}$

  • SPEC：实用基准测试程序集

    基于现有应用程序的一套标准化源代码作为基准的测试程序集;
    方便对计算机性能的比较；

    设置一个参考计算机，对于每一个参考程序，对所有的计算机均可计算出性能比，对于各个程序的性能比取几何平均值$\sqrt[n]{\prod_{i=1}^{n}SPECratio_i}$即可算出总体性能比；

性能的改进

  • 提高并行的层次

    • 系统级：使用多处理器
    • 指令级：流水线
    • 操作级：并行加法器，组相连cache，流水级功能部件

  • 局部性原理（经验性质的原理）

    • 时间局部性：最近访问过的项目可能近期内再次被使用
    • 空间局部性：最近访问过的数据地址附近可能会再次使用
    • 注重经常性事件：Amdahl定律
      $ Speedup(A)=\frac {改进A前时间}{改进Ａ后时间}$
      $ F(A)=A在程序运行的时间在程序Pro中所占比例$
      $ Speedup(Pro)=\frac{1}{1-F(A)+\frac{F(A)}{Speedup(A)}}$
      $ Speedup(Pro)<\frac{1}{1-F(A)}$，这说明性能提高的瓶颈在于改进比例；
      $ Speedup(Pro)$越大，改进越优秀；

第二章：计算机的数值与编码

补码

  • 对于一个r位数d，对应补码为$f(d)=\begin{cases} &\text d ,d>0;\ &\text (2^r-1)-|d|+1 ,d>0;\end{cases} $；
  • 对于正数而言，补码等于本身，对于负数而言，补码等于其绝对值的反码加1；
  • 已知补码，若最高位为0，表示正数，原码等于补码；若最高位为1，原码为补码减1后取反得到的正数的相反数；
  • 补码表示的范围是$[100..0,011..1]$,也即$[-2^{n-1},2^{n-1}-1]$;
  • 转化为更高位的数：符号拓展&零拓展
    • 符号拓展：在最高位前面增加相应的符号位（正0负1），适用于有符号数；
    • 零拓展：在最高位前面增加0，适用于无符号数；
  • 溢出：符号位相反两数相加不会溢出；溢出位交给异常处理；
  • 乘除法基于加减法和移位运算实现；
  • 移位
    • 左移：右端补0；
    • 右移：
      • 逻辑右移：左端补0；
      • 算数右移：左端补符号位；
  • 逻辑与、或、非、异或：实现某些位的变化；

浮点数的规格化

  • 二进制浮点数算数标准 IEEE-754 约定了小数点的位置
  • 浮点数$(-1)^s\times (1.M_2)\times 2^E$ 分别为 符号位（1位） 阶码（8位/32位 或者 11位/64位） 尾数（23位/32位 或者 52位/64位） ,也即$[s][E+2^{n-1}-1][M_2]$;
  • 小数点左边的数不必储存，约定始终为1
  • 尾数按小数部分的真值进行存储
  • 指数真实值需要加上固定偏移量$2^{n-1}-1$进行存储，$n$为阶码字段位数（即一般为127或1023）
  • 阶码不能全0不能全1（属于保留数字，无穷或者无效数字）

浮点数的加减

  • 对阶操作
    小数点位置对齐（阶码相等），小阶向大阶看看齐，隐藏位右移
  • 尾数运算
    增加隐藏位，进行加减运算
  • 规格化处理
    重新转化为一个规格化浮点数

实例：

对于13位二进制数（1位符号位，5位阶码，7位尾数）$x=1.0110011\times2^9,y=1.1101101\times2^7$,计算$x+y$;

过程：

阶码的固定偏移量为$2^4-1=15$;因而$x$的阶码表示为24（11000），$y$的阶码表示为22（10110）；

$x$的编码为$[0][11000][0110011]$,$y$的编码为$[0][10110][1101101]$;

将$y$阶码向$x$对齐，隐藏位右移得$[0][11000][0111011]$;

尾数相加$01.0110011+00.0111011=01.1101110$,得$x+y=[0][11000][1101110]=1.1101110\times2^9$;这已经是一个规格数了；

浮点数的乘除

  • 阶码定点加减
  • 尾数乘除
  • 规格化处理

字符的表示

  • 二进制编码
  • 美国信息交换标准码（ASCII）： 表示现代英文和符号，但是过于有限
  • 统一码（Unicode） ：每个符号要用两个或多个字节表示，但存在浪费，十六进制表示
  • UTF-8 ：变长的编码方式，用1-4个字节表示符号，二进制表示

第三章：计算机芯片的数字电路基础

  • 输入输出逻辑关系：与/或/非
  • 多输入端和一个输出端
  • 利于封装组合和模块化不关心内部电路实现
  • 输入变化存在延迟时间（基于晶体管等电气特性）

逻辑代数基础

Axioms

  1. If $x\neq 0$, $x=1$ ;if $x\neq1$, $x=1$
  2. If $x=0$ , $\overline{x}=1$ ;if $x=1$ ,$\overline{x}=0$
  3. $0 \cdot 0=0,0 \cdot 1=0, 1\cdot 0=0,1\cdot 1=1 $
  4. $0+0=0,1+0=1,0+1=1$,$1+1=1$

Notices

  • $1+A=1$
  • $A+A=A$
  • $A+BC=(A+B)\cdot (A+C)$
  • $\overline{A+B}=\overline{A}\cdot \overline{B}$
  • $A+\overline{A}B=A+B$
  • $A+AB=A$
  • $AB+\overline{A}C+BCDEF=AB+\overline{A}C$

反演定理

与运算和或运算置换，取反运算不变，变量取反，计算顺序不变，得到反演逻辑式；
两相等逻辑式的反演逻辑式相等；

对偶定理

与、或运算置换，0、1置换，得到对偶式；
两相等逻辑表达式的对偶式相等；

最大项之积和最小项之和

最小项编码依据是真值为1；

最大项编码依据是真值为0；

标准形式:
$F=\sum_{}{m(i_1,i_2,…,i_k)}=\prod_{}{M(j_1,j_2,…,j_t)}$

反复利用$B=(A+\overline {A})B$， $A+BC=(A+B)(A+C)$即可；

在$Carnot$ 图中，每个格子进行$0～2^n-1$的编码，相邻两个格子编码$Haming$距离为1(换言之，构成一个Gray码)，用尽量少的框去框尽可能多的1，方便得到更简单的逻辑电路图

利用标准形式可以判断两个逻辑函数是否相等，即逻辑函数相等那么他们的标准形式等价

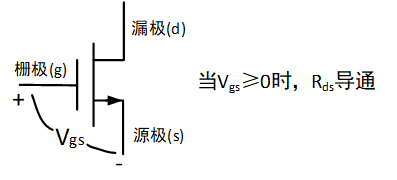
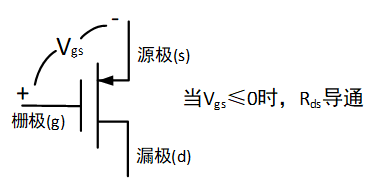
逻辑序列

CMOS逻辑

  • 3.5～5V：高态

  • 1.5～3.5V：未定义逻辑电平

  • 0～1.5V：低态

  • NMOS和PMOS晶体管共用形成CMOS逻辑

    • 对于NMOS，$V_{gs}=0V$断开，$V_{gs}=5V$导通；

      image-20231024232258414

    • 对于PMOS，$V_{gs}=0V$断开，$V_{gs}=-5V$导通；

      image-20231024232343077

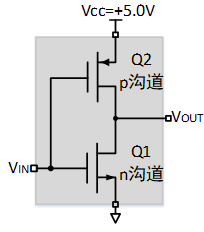
非门

仅用了一个NMOS管和一个PMOS管；

image-20231024232819276

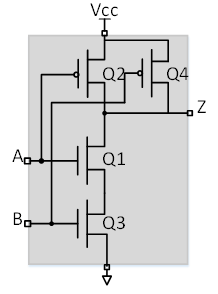
与非门、与门

用了k个NMOS管和k个PMOS管（k为输入端口数目，最多输入端为6个），下图是k=2的CMOS电路：

image-20231024233404303

通过级联一个非门可以得到与门，尽量能使用与非运算表示的逻辑不用与运算的道理就在此处；

或非门

将与非门中NMOS与PMOS互换可以得到或非门，类似的实例不再展示（最多输入端为4个）：

同样级联一个非门可以得到或门；

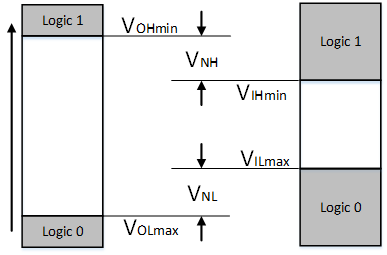
静态电气特性

$V_{OHmin}$：输出为高态时的最小输出电压，一般为VCC-0.1V；

$V_{OLmax}$：输出为低态时的最大输出电压，一般为地+0.1V；

$V_{IHmin}$：保证能被识别为高态的最小输入电压，一般为VCC的70%；

$V_{ILmax}$：保证能被识别为低态的最大输入电压，一般为VCC的30%;

image-20231024234337257

进行级联时应该满足相应大小关系；

不用的输入端不允许悬空不接；

动态电器特性

  1. 转换时间

    上升时间$t_r$和下降时间$t_f$图示,近似等于器件电阻和负载电容的乘积；

    启示：尽可能使的信号驱动的输入端最少以减少负载电容；

    image-20231026105142094

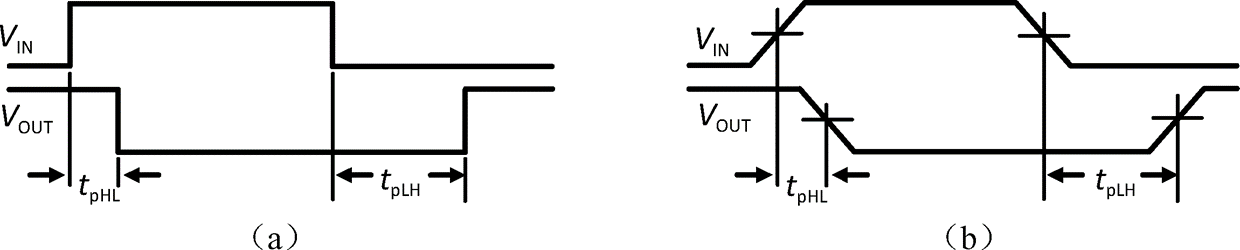
  2. 传播延迟

    输入信号变化到输出信号变化所需时间；

    $t_p=t_{pLH}+t_{pHL}$；

    启示：尽可能使电路简单化以降低传播延迟；

    image-20231026101525221

  3. 动态功耗

    电路处于非稳态时，MOS部分导通产生的漏电流带来功耗，是总功耗的主要部分；

    $P_D=(C_{PD}+C_L)V_{CC}\times f$ ;

Verilog

第四章：计算机芯片的基本电路组成

组合逻辑电路

注意与非门、或非门比较简单，注意转化为与非和或非的组合；

Multiplex多路选择器

最简单的多路选择器（Multiplexer）是1位二选一多路器。

当输入S为高电平时，输入Y的值为输入A1的值；

当输入S为低电平时，输入Y的值为输入A0的值;
$$
Y=\overline{S}A_0+SA_1=\overline{\overline{\overline{S}A_0}\cdot \overline{SA_1}}
$$

1
2
3
4
5
6
7
8
9
10
11
module MUX2X1(
    input A0,
    input A1,
    input S,
    output Y
);
    not i0(S_n,S);
    nand i1(A0S,A_0,S);
    nand i2(A1S,A_1,S_n);
    nand i3(Y,A0S,A1S);
endmodule

对于32位二选一选择器功能描述风格代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
module MUX2X32(A_0,A_1,S,Y);
    input[31:0] A_0,A_1;
    input[0:0] S;
    output[31:0] Y;

        function[31:0] select;
            input[31:0] A,B;
            input[0:0] S;
                case(S) 
                    1'b1:select=A;
                    1'b0:select=B;
                endcase
        endfunction
    
    assign Y=select(A_1,A_0,S);
endmodule

module MUX2X32(A_0,A_1,S,Y);
    input[31:0] A_0,A_1;
    input[0:0] S;
    output[31:0] Y;

    assign Y=S==1'b0?A_0:A_1;
endmodule

也可以用门级电路实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
module MUX2X32(
    input[31:0]A_0,
    input[31:0]A_1,
    input[0:0]S,
    output[31:0]Y
);
    MUX2X1 i0(
        .A_0(A_0[0]),
        .A_1(A_1[0]),
        .S(S),
        .Y(Y[0])
     ); 
    MUX2X1 i1(
        .A_0(A_0[1]),
        .A_1(A_1[1]),
        .S(S),
        .Y(Y[1])
     ); 
    ...//篇幅略长，但好像没找到别的办法了？
    MUX2X1 i31(
        .A_0(A_0[31]),
        .A_1(A_1[31]),
        .S(S),
        .Y(Y[31])
     );        
endmodule

对于32位四选一选择器实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
module MUX2X32(A_0,A_1,A_2,A_3,S,Y);
    input[31:0] A_0,A_1,A_2,A_3;
    input[1:0] S;
    output[31:0] Y;

        function[31:0] select;
            input[31:0] A,B,C,D;
            input[0:0] S;
                case(S) 
                    2'b00:select=A;
                    2'b01:select=B;
                    2'b10:select=C;
                    2'b11:select=D;
                endcase
        endfunction
    
    assign Y=select(A_0,A_1,A_2,A_3,S);
endmodule

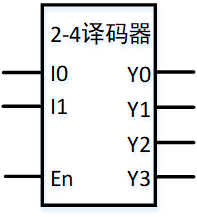
Decode译码器

$n-2^n$二进制译码器，其n个输入端信号形成一个n位的二进制数值，其$2^n$个输出端中对应序号的输出端为高电平输出，其余$2^n-1$个输出端输出低电平信号;

带使能端En的译码器真值表如下

$En$ $I_1$ $I_0$ $Y_0$ $Y_1$ $Y_2$ $Y_3$
0 x x 0 0 0 0
1 0 0 1 0 0 0
1 0 1 0 1 0 0
1 1 0 0 0 1 0
1 1 1 0 0 0 1

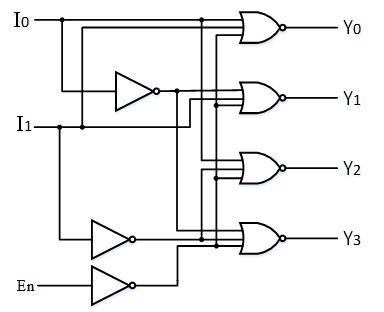
image-20231026112149809

image-20231026112209039

DEC2T4E门级电路实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
module DEC2T4E(I0,I1,En,Y0,Y1,Y2,Y3);
    input I0,I1,En;
    output Y0,Y1,Y2,Y3;

    not i0(I0_n,I0);
    not i1(I1_n,I1);
    not i2(En_n,En);
    
    nor i3(YY0,I0,I1,En_n);
    nor i4(YY1,I0,I1_n,En_n);
    nor i5(YY2,I0_n,I1,En_n);
    nor i6(YY3,I0_n,I1_n,En_n);
endmodule

DEC5T32E实现如下;

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
module DEC5T32E(I,En,Y);
    input[4:0] I;
    input En;
    output[31:0] Y;
    
	function[31:0] dec;
		input[4:0] I;
		input En;

		if(En)  
		    begin
		    case(I)
		    5'b0_0000 : dec = 32'b0000_0000_0000_0000_0000_0000_0000_0001 ;
		    5'b0_0001 : dec = 32'b0000_0000_0000_0000_0000_0000_0000_0010 ;
		    5'b0_0010 : dec = 32'b0000_0000_0000_0000_0000_0000_0000_0100 ;
			5'b0_0011 : dec = 32'b0000_0000_0000_0000_0000_0000_0000_1000 ;
			5'b0_0100 : dec = 32'b0000_0000_0000_0000_0000_0000_0001_0000 ;
			5'b0_0101 : dec = 32'b0000_0000_0000_0000_0000_0000_0010_0000 ;
			5'b0_0110 : dec = 32'b0000_0000_0000_0000_0000_0000_0100_0000 ;
			5'b0_0111 : dec = 32'b0000_0000_0000_0000_0000_0000_1000_0000 ;
			5'b0_1000 : dec = 32'b0000_0000_0000_0000_0000_0001_0000_0000 ;
			5'b0_1001 : dec = 32'b0000_0000_0000_0000_0000_0010_0000_0000 ;
			5'b0_1010 : dec = 32'b0000_0000_0000_0000_0000_0100_0000_0000 ;
			5'b0_1011 : dec = 32'b0000_0000_0000_0000_0000_1000_0000_0000 ;
			5'b0_1100 : dec = 32'b0000_0000_0000_0000_0001_0000_0000_0000 ;
			5'b0_1101 : dec = 32'b0000_0000_0000_0000_0010_0000_0000_0000 ;
			5'b0_1110 : dec = 32'b0000_0000_0000_0000_0100_0000_0000_0000 ;
			5'b0_1111 : dec = 32'b0000_0000_0000_0000_1000_0000_0000_0000 ;
			5'b1_0000 : dec = 32'b0000_0000_0000_0001_0000_0000_0000_0000 ;
			5'b1_0001 : dec = 32'b0000_0000_0000_0010_0000_0000_0000_0000 ;
			5'b1_0010 : dec = 32'b0000_0000_0000_0100_0000_0000_0000_0000 ;
			5'b1_0011 : dec = 32'b0000_0000_0000_1000_0000_0000_0000_0000 ;
			5'b1_0100 : dec = 32'b0000_0000_0001_0000_0000_0000_0000_0000 ;
			5'b1_0101 : dec = 32'b0000_0000_0010_0000_0000_0000_0000_0000 ;
			5'b1_0110 : dec = 32'b0000_0000_0100_0000_0000_0000_0000_0000 ;
			5'b1_0111 : dec = 32'b0000_0000_1000_0000_0000_0000_0000_0000 ;
			5'b1_1000 : dec = 32'b0000_0001_0000_0000_0000_0000_0000_0000 ;
		    5'b1_1001 : dec = 32'b0000_0010_0000_0000_0000_0000_0000_0000 ;
			5'b1_1010 : dec = 32'b0000_0100_0000_0000_0000_0000_0000_0000 ;
			5'b1_1011 : dec = 32'b0000_1000_0000_0000_0000_0000_0000_0000 ;
			5'b1_1100 : dec = 32'b0001_0000_0000_0000_0000_0000_0000_0000 ;
			5'b1_1101 : dec = 32'b0010_0000_0000_0000_0000_0000_0000_0000 ;
		    5'b1_1110 : dec = 32'b0100_0000_0000_0000_0000_0000_0000_0000 ;
			5'b1_1111 : dec = 32'b1000_0000_0000_0000_0000_0000_0000_0000 ;
			default   : dec = 32'b0000_0000_0000_0000_0000_0000_0000_0000 ;
            endcase
		    end
    	else  dec = 32'b0000_0000_0000_0000_0000_0000_0000_0000 ;
	endfunction

	assign Y=dec(I,En);
endmodule

Encode编码器

将输入信号的每一个高、低电平信号编制成其对应的二进制编码;

如果出现多个输入高电平时，编码器产生最高优先级的输入端对应的编号。我们把这样的编码器叫做优先级编码器；

优先级编码器还需要一个额外的输出端IDLE来标识当前的输入信号是否为全0;

$ I_7$ $I_6$ $I_5$ $I_4$ $I_3$ $ I_2$ $ I_1 $ $ I_0 $ $ Y_2 $ $ Y_1 $ $ Y_0 $ $Idle$
1 x x x x x x x 1 1 1 0
0 1 x x x x x x 1 1 0 0
0 0 1 x x x x x 1 0 1 0
0 0 0 1 x x x x 1 0 0 0
0 0 0 0 1 x x x 0 1 1 0
0 0 0 0 0 1 x x 0 1 0 0
0 0 0 0 0 0 1 x 0 0 1 0
0 0 0 0 0 0 0 1 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 1

ENC8T3I实现如下（尚未验证）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
module ENC8T3I(
    input [7:0] I,
    output [2:0] Y,
    output [0:0] Idle
);
	if(I[7]) begin Y=3'b111; Idel=1'b0; end
	else if(I[6]) begin assign Y=3'b110; assign Idel=1'b0; end
	else if(I[5]) begin assign Y=3'b101; assign Idel=1'b0; end
	else if(I[4]) begin assign Y=3'b100; assign Idel=1'b0; end
	else if(I[3]) begin assign Y=3'b011; assign Idel=1'b0; end
	else if(I[2]) begin assign Y=3'b010; assign Idel=1'b0; end
	else if(I[1]) begin assign Y=3'b001; assign Idel=1'b0; end
	else if(I[0]) begin assign Y=3'b000; assign Idel=1'b0; end
	else begin assign Y=3'b000; assign Idel=1'b0; end
	
endmodule

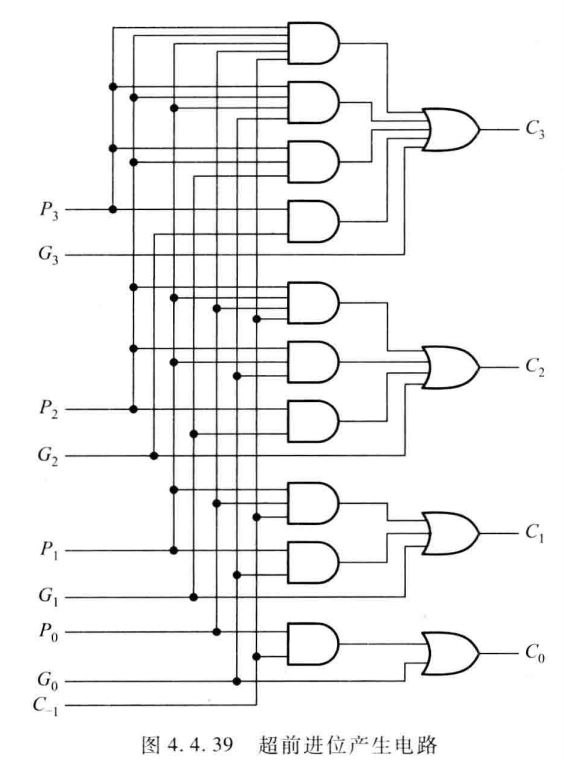
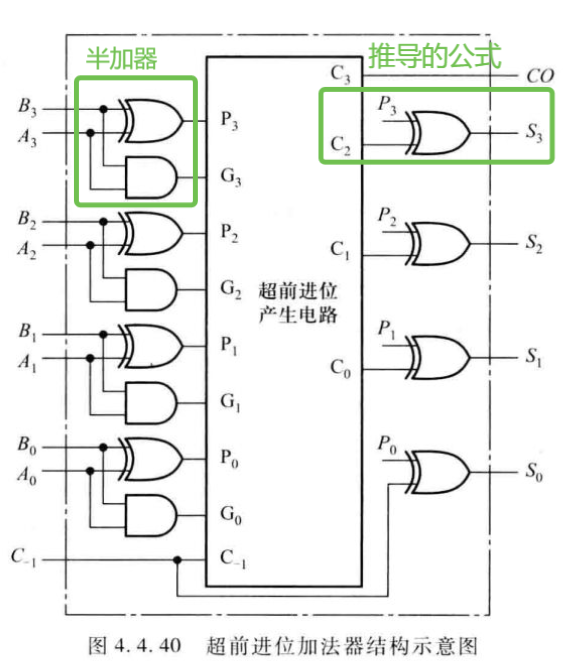
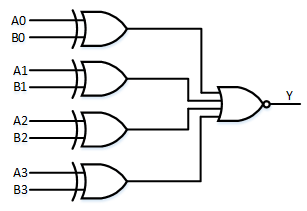
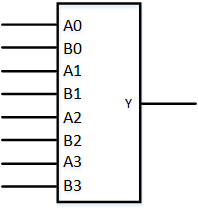
Adder 加法器

如果能通过逻辑电路直接得出全加器每一位的进位信号就无需从最低位向最高位逐级传递进位信号了，这样的加法器叫做超前进位（Carry Lookahead）加法器；

（图源）

四位超前进位加法器门级电路实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
module CLA_4(
    input[3:0] X,
    input[3:0] Y,
    input[0:0] Cin,
    output[3:0] S,
    output[0:0] Cout
);
    wire[3:0] P=X|Y;
    wire[3:0] G=X&Y;
    wire[3:0] Gn=~G;

    and i1(P0Gn0,P[0],Gn[0]);
    xor(S[0],P0Gn0,Cin);
    nand(P0Cin0,P[0],Cin);
    nand(Cout0,Gn[0],P0Cin0);

    and(P1Gn1,P[1],Gn[1]);
    xor(S[1],P1Gn1,Cout0);
    nand(P1P0Cin0,P[1],P[0],Cin);
    nand(P1G0,P[1],G[0]);
    nand(Cout1,Gn[1],P1G0,P1P0Cin0);

    and(P2Gn2,P[2],Gn[2]);
    xor(S[2],P2Gn2,Cout1);
    nand(P2P1P0Cin0,P[2],P[1],P[0],Cin);
    nand(P2P1G0,P[2],P[1],G[0]);
    nand(P2G1,P[2],G[1]);
    nand(Cout2,Gn[2],P2G1,P2P1G0,P2P1P0Cin0);

    and(P3Gn3,P[3],Gn[3]);
    xor(S[3],P3Gn3,Cout2);
    nand(P3P2P1P0Cin0,P[3],P[2],P[1],P[0],Cin);
    nand(P3P2P1G0,P[3],P[2],P[1],G[0]);
    nand(P3P2G1,P[3],P[2],G[1]);
    nand(P3G2,P[3],G[2]);
    nand(Cout,Gn[3],P3G2,P3P2G1,P3P2P1G0,P3P2P1P0Cin0);

endmodule

16位组间串行进位加法器实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
module CLA_16 (X, Y, Cin, S, Cout);
    input [15:0] X, Y;
    input Cin;
    output [15:0] S;
    output Cout;
    wire Cout0, Cout1, Cout2;
    CLA_4 add0 (X[3:0], Y[3:0], CIN, S[3:0], Cout0);
    CLA_4 add1 (X[7:4], Y[7:4], Cout0, S[7:4], Cout1);
    CLA_4 add2 (X[11:8], Y[11:8], Cout1, S[11:8], Cout2);
    CLA_4 add3 (X[15:12], Y[15:12], Cout2, S[15:12], Cout);
endmodule

32位组间串行进位加法器实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
module CLA_32 (X, Y, Cin, S, Cout);
    input [31:0] X, Y;
    input Cin;
    output [31:0] S;
    output Cout;
    wire Cout0, Cout1, Cout2,Cout3, Cout4, Cout5,Cout6, Cout;
    
    CLA_4 add0 (X[3:0], Y[3:0], CIN, S[3:0], Cout0);
    CLA_4 add1 (X[7:4], Y[7:4], Cout0, S[7:4], Cout1);
    CLA_4 add2 (X[11:8], Y[11:8], Cout1, S[11:8], Cout2);
    CLA_4 add3 (X[15:12], Y[15:12], Cout2, S[15:12], Cout3);
    CLA_4 add4 (X[19:16], Y[19:16], Cout3, S[19:16], Cout4);
    CLA_4 add5 (X[23:20], Y[23:20], Cout4, S[23:20], Cout5);
    CLA_4 add6 (X[27:24], Y[27:24], Cout5, S[27:24], Cout6);
    CLA_4 add7 (X[31:28], Y[31:28], Cout6, S[31:28], Cout);
    
endmodule

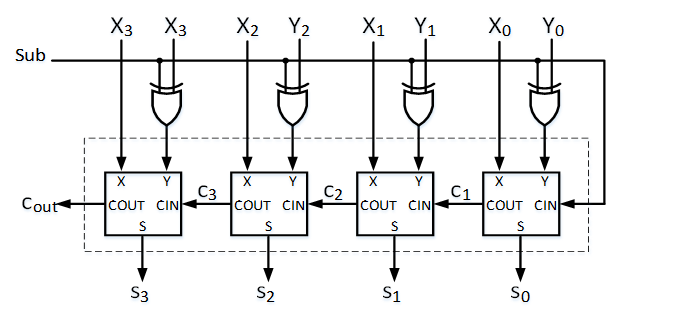
Adder-Subtracter加减器

利用加法器可实现减法运算；

可在串行进位加法器的基础上对其中一个输入向量的每个位信号增加了一个异或门，实现：

当输入信号Sub为低电平时，完成加法运算，当输入信号Sub为高电平时，完成减法运算；

image-20231026123543859

16位组间串行进位加减器实现如下：

1
2
3
4
5
6
7
8
module ADDSUB_16 (X, Y, Sub, S, Cout);
   input [15:0] X, Y;
   input Sub;
   output [15:0] S;
   output Cout;
   CLA_16 adder0 (X, Y^{16{Sub}}, Sub, S, Cout);
endmodule

32位组间串行进位加减器实现如下：

1
2
3
4
5
6
7
module ADDSUB_32 (X, Y, Sub, S, Cout);
   input [31:0] X, Y;
   input Sub;
   output [31:0] S;
   output Cout;
   CLA_32 adder0 (X, Y^{32{Sub}}, Sub, S, Cout);
endmodule

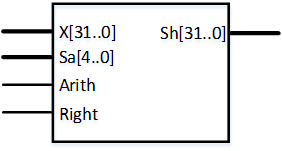
Shifter 移位器

  • X是32位移位前的输入信号；Sh是32位移位后的输出信号；

  • 输入Sa表示移位位数，5位宽（移位位数为0~31位）；

  • 输入Arith为高电平表示进行算术移位，为低电平表示进行逻辑移位；

  • 输入Right为高电平表示向右移位，为低电平表示向左移位；

    image-20231026232851309

  • 根据输入移位二进制表示，将移位器分成5级，分别进行移位16，8，4，2，1位；

（未测试）32位移位器的粗略实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
module SHIFTER_32 (X, Sa, Arith, Right, Sh);
   input [31:0] X;
   input [4:0] Sa;
   input Arith, Right;
   output [31:0] Sh;
   wire [31:0] T4, S4, T3, S3, T2, S2, T1, S1, T0;
   wire a = X[31] & Arith;
   wire [15:0] e = {16{a}};
   parameter z = 16'b0;
   wire [31:0] L1u, L1d, L2u, L2d, L3u, L3d, L4u, L4d, L5u, L5d;
   assign L1u = {X[15:0] ,z};
   assign L1d = {e, X[31:16] };
   MUX2X32 M1l (L1u, L1d, Right, T4);
   MUX2X32 M1r (X, T4, Sa[4], S4); 
   //完成第1级多路器实现
                …
endmodule

Comparator 比较器

按位异或结果每一位都是0说明相同，输出高电平；否则不同，输出低电平；

image-20231026233710687

image-20231026233724350

（未测试）CPT4的基本实现

1
2
3
4
5
6
7
8
9
10
module CPT4 (A, B, Y);
input [3:0] A, B;
output Y;
xor  i0 (D0, A[0], B[0]);
xor  i1 (D1, A[1], B[1]);
xor  i2 (D2, A[2], B[2]);
xor  i3 (D3, A[3], B[3]);
nor  i4 (Y, D0, D1, D2, D3);
endmodule

Extender 数据拓展器

有两种方式：符号拓展，零拓展；

数据扩展模块需要一个数据输入端、一个扩展方式选择端和一个数据输出端；

image-20231027093832127

（未测试）16位数拓展32位数具体实现;

1
2
3
4
5
6
7
8
9
10
11
12
module EXT16T32 (X, Se, Y);
input [15:0] X;
input B;
output Y;
wire [31:0] E0, E1;
wire [15:0] e = {16{X[15]}};
parameter z = 16ˊb0;
assign E0 = {z, X};
assign E1 = {e, X};
MUX2X32 i(E0, E1, Se, Y);
endmodule

时序逻辑电路

D锁存器

image-20231027094316742

D En Q Qn
1 1 1 0
0 1 0 1
X 0 维持不变 维持不变

D锁存器不会出现其输出Q和Qn同时为高电平的情况，从而也就避免了当D锁存器关闭时其输出进入不可预知状态

具体实现（未测试）

1
2
3
4
5
6
7
8
9
10
11
12
module D_Latch (D, En, Q, Qn);
input D, En;
output Q, Qn;
wire Sn, Rn, Dn;
not i0 (Dn, D);
nand i1 (Sn, D, En);
nand i2 (Rn, En, Dn);
nand i3 (Q, Sn, Qn);
nand i4 (Qn, Q, Rn); 
//这两行代码实现的是Sn-Rn锁存器
endmodule

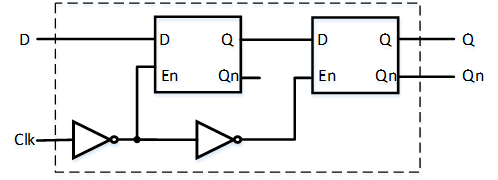
D触发器

在计算机芯片内部，我们往往需要通过输入的时钟边沿信号（时钟的上升沿或下降沿）去控制D锁存器的开闭，把这种用时钟边沿控制D锁存器中存储内容的元件叫做D触发器；

用两个D锁存器和两个非门构成了一个上升沿触发式D触发器；

image-20231027094702910

D Clk Q Qn
1 上升沿 1 0
0 上升沿 0 1
X 0 维持不变 维持不变
X 1 维持不变 维持不变

具体实现（未测试）

1
2
3
4
5
6
7
8
9
10
11
module D_FF (D, Clk, Q, Qn);
input D, Clk;
output Q, Qn;
wire Clkn, Q0, Qn0;
not i0 (Clkn, Clk);
D_Latch d0 (D, Clkn, Q0, Qn0); 
//主锁存器
D_Latch d1 (Q0, Clk, Q, Qn); 
//从锁存器
endmodule

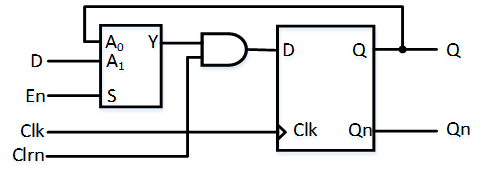
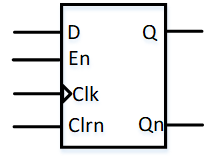
带使能端和清零端的上升沿式D触发器

image-20231027094948639

D Clk En Clrn Q Qn
1 上升沿 1 1 1 0
0 上升沿 1 1 0 1
X X 0 1 维持不变 维持不变
X 上升沿 X 0 0 1

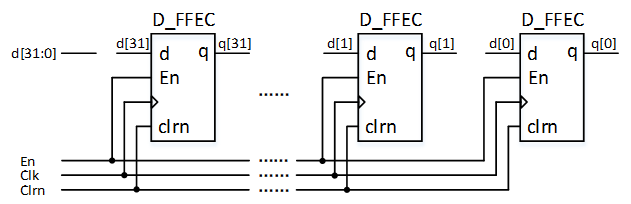
32位通用寄存器

image-20231027095212431

1
2
3
4
5
6
7
8
9
10
module D_FFEC32 (D, Clk, En, Clrn, Q, Qn);
input [31:0 ] D;
input Clk, En, Clrn;
output [31:0] Q, Qn;
D_FFEC d0 (D[0], Clk, En, Clrn, Q[0], Qn);
D_FFEC d1 (D[1], Clk, En, Clrn, Q[1], Qn);
…
D_FFEC d31 (D[31], Clk, En, Clrn, Q[31], Qn);
endmodule