第二章:认识数据
第二章:认识数据
2.1 数据对象与属性类型
- 数据对象 = 样本/实例/数据点/对象,用属性描述
2.1.1 什么是属性
- 属性attribute,维dimension,特征feature,变量variable
2.1.2 标称属性NominalAttribute
- 标称属性的值仅仅只是不同的名字
- 众数、熵、列联相关、$\chi^2$检验是有意义的
2.1.3 二元属性BinaryAttribute
- 只有两个状态0,1
- 对称的
- 非对称的:重要的值通常比较少出现,通常用1表示,例如化验结果中的阳性
2.1.4 序数属性OrdinalAttribute
- 序数属性的值提供足够的信息确定对象的序
- 中值、百分位、秩相关、游程检验、符号检验是有意义的
2.1.5 数值属性NumericAttribute
- 区间属性IntervalAttribute
- 存在测量的单位
- 均值、标准差、皮尔逊相关、$T$检验和$F$检验是有意义的
- 比率RatioAttribute
- 关注差和比率
- 几何平均、调和平均、百分比变差是有意义的
2.1.6 离散属性与连续属性
- 离散属性DiscreteAttribute
- 有限或无限可数个值
- 常表示为整数变量或字符串变量
连续属性ContinuousAttribute - 属性值为实数
- 实践中, 实数只能用有限位数字的数度量和表示.
- 连续属性一般用浮点变量表示.
2.2 数据的基本统计描述
2.2.1 中心度量趋势
- 均值:$avg(x)=\frac{\sum_{i=1}^{N}x_i}{N}$
- 加权均值:$avg(x)=\frac{\sum_{i=1}^{N}\omega_ix_i}{\sum_{i=1}^{N}\omega_i}$
- 截尾均值:减少极端值的影响
- 中位数:线性插值估计
- 找到中位数区间$S=[L_1,L_1+width]
- S区间频数为$freq_{mid}$,低于S的所有区间频数和为$\Sigma$
- 估计$Median = L_1+ width \cdot \frac{N/2-\Sigma}{freq_{mid}}$
- 众数:对于非单峰数据,有如下经验:$mean-mode\sim 3*(mean-median)$
2.2.2 度量数据的散布
- 极差:$max-min$
- 四位分数:将数据分布划分为4个相等部分,分界点为$Q_1,Q_2(\text{中位数}),Q_3$
- 四分位数极差:给出数据中间一半的覆盖范围,$IDQ=Q_3-Q_1$
- 方差: $\sigma^2 = \frac{1}{N}\sum_{i=1}^{N}(x_i-\bar{x})^2$
- 标准差:度量均值的发散,$\sigma= \sqrt{\frac{1}{N}\sum_{i=1}^{N}(x_i-\bar{x})^2}$
- 五数概括$summary(x)=[min,Q1,median,Q3,max]$
- 盒图
2.2.3 数据的基本统计描述的图形显示
- 分位数图
- 观察单变量数据分布
- 每个观测值和某个百分数配对

- 分位数-分位数图
- 刻画一个分布到另一个分布是否有漂移

- 直方图
- 刻画数据的整体分布情况
numpy.hist()
- 散点图
- 数据的具体分布(<=3维)

2.3 数据可视化
2.3.1 基于像素的可视化技术
- 空间填充曲线
2.3.2 几何投影可视化技术
- 平行坐标技术
2.3.3 基于图符的可视化技术
- Chernoff脸
- 人物线条画
2.3.4 层次可视化技术
- “World-within-world”技术
- 树图
2.3.5 可视化复杂对象和关系
- 标签云tag-cloud
2.4 度量数据的相似性和相异性
相似性和相异性都被称作邻近性
2.4.1 数据矩阵和相异性矩阵
基于内存的聚类和最邻近算法基于两种数据结构:
- 数据矩阵dataMatrix
- 对象-属性two_mode
- 相异性矩阵dissmilaratyMatrix
- 对象-对象single_mode
- 对称的,对角线是0
- $sim(i,j)=1-d(i,j)$
2.4.2 标称属性的邻近性度量
相异性计算标准:
- 不匹配率计算:$d(i,j)=\frac{p-m}{p}$
- 将标称属性用非对称的二元属性编码
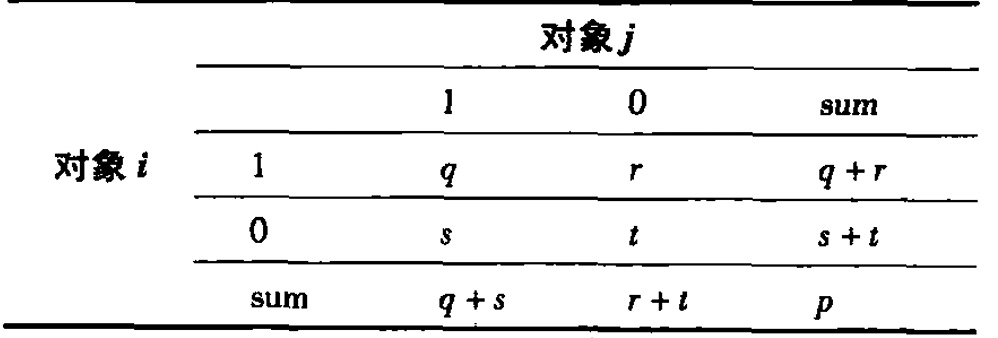
2.4.3 二元属性的邻近性度量
- 对称二元属性:
- 每个状态同样重要,$d(i,j)=\frac{r+s}{q+r+s+t}$
- 非对称二元属性:
- 正匹配比负匹配更重要
$d(i,j)=\frac{r+s}{q+r+s}$
- 正匹配比负匹配更重要
2.4.4 数值属性相异度:闵可夫斯基距离
对数据对象$i=(x_{i1},x_{i2},…,x_{ip}),j=(x_{j1},x_{j2},…,x_{jp})$,各维权重为$w=(w_1,w_2,…,w_p)$,Minkowski距离:$d(i,j)=\sqrt{q}{\sum_{k=1}^{p}{w_i(x_{ik}-x_{jk})^q}}$
注意,各维等价时,p=1称为Manhattan距离,p=2称为Euclidean距离
2.4.5 序数属性的相异性度量
变量$f$具有$M_f$个状态,变量的值映射为秩,即某个对象变量$f_i$,值为$x_{if}$,秩为$r_i$,相异度计算用区间标度变量处理:$z_i=\frac{r_{if}-1}{M_f-1}$,即用linspace(0,1,Mf)代表每个点
2.4.6 混合属性的相异度
数据集包括p个混合属性,指示符$\delta_{ij}^{f}=0$当且仅当$x_i,x_j$缺失或者在非对称二元属性中形成负匹配
根据属性的贡献计算
$d(i,j)=\frac{\sum_{i=1}^{p}\delta_{ij}^{p}d_{ij}}{\sum_{i=1}^{p}\delta_{ij}^{p}}$
f是数值的:$d_{ij}^{f}=\frac{|x_{if}-x_{jf}|}{max_hx_{hf}-min_hx_{hf}}$,h取遍f非缺失对象
f是标称的或二元的:$d_{ij}=1\ if\ x_{if}=x_{jf}$
f是序数的:$z_i=\frac{r_{if}-1}{M_f-1}$
2.4.7 余弦相似性
对于待比较的向量$x,y$,使用余弦度量$sim(x,y)=\frac{x\cdot y}{||x||\ ||y||}$
