离群点(Outlier)检测

Posted on

离群点(Outlier)和异常(Anomaly)检测

Background

异常数据通常作为噪音而忽略，但是在欺诈检测，入侵检测等领域，离群点能带来新的启发。

Content

概念

离群点：显著不同于其它数据对象，好像它是被不同的机制产生的一样；

噪声：观测变量的随机性产生；

分类

  • 全局离群点：显著地偏移其他对象
  • 情景离群点：依赖情景属性和行为属性，例如夏天的28℃和冬天的28℃
    • 局部离群点：密度偏离所在局部区域的密度；
  • 集体离群点：数据集中的一个子集偏移整个数据集；

挑战

  • 合适的建模
  • 如何分辨噪声和离群点？
  • 可解释性，针对应用

监督，半监督和无监督的方法

pass

基于统计学的检测

事先对数据集进行分布上的假设，采用不一致性检验(Discordancy test)；

例如经验告诉我们，假设数据集服从正态分布，需要参数如下：

  • 数据集参数: 例如, 假设的数据分布
  • 分布参数: 例如平均值和方差
  • 和预期的孤立点的数目

缺点：

  • 难以挖掘多维属性；
  • 数据集分布未知，但有效性高度依赖于给定数据所做的统计模型假设是否成立。
  • 不保证所有离群点被发现；

基于距离的检测

数据对象的给定半径的邻域内，如果没有足够多的邻居，那么被认定为离群点；

  • 距离阈值$r$;
  • 分数阈值$\pi$;
  • 距离度量$dis(o,o’)$;

若$o$被认为是数据集$D$中的$DB(r,\pi)$离群点，即
$$
\frac{|{o’|dis(o,o’)}|}{|D|}\le \pi
$$
常见算法：

  • K-d Tree
  • 嵌套循环：遍历对象，计算对象半径内的邻居数，若中途超出阈值提前退出；
  • 一种cell-based算法：先验性质剪枝

注意：$o_1,o_2$并不能被基于距离的算法检测到离群

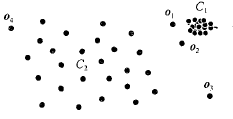
image-20240527155532971

基于偏离的检测

检查对象的主要特征，与给出的描述偏离大的对象被认为是离群点；

基于密度的检测

非离群对象周围的密度与其邻域周围密度类似，而离群点密度显著不同于邻域周围的密度；

  • 对象$o$的$k-distance$:第$k$个最近邻之间的距离$dis_k(o)$；

    • 注意集合$N_k(o)={o’\in D-{o}|dis(o,o’)\le dis_k(o)}$可能大小超过$k$;

  • 对象$p$相对于对象$o$的可达距离：$reachDis_k(p,o)=\max{dis_k(o),dis(p,o)}$

  • 对象$o$的局部可达密度:$lrd_k(o)=\frac{|N_k(o)|}{\sum_{p\in D} reachDis_k(p,o)}$

    • 对象$o$的局部异常因子（Local Outlier Factor）:

      $LOF_k(o)=\frac{1}{|N_k(o)|}{\sum_{o’\in N_k(o)}\frac{lrd_k(o’)}{lrd_k(o)}}$​

      • 表示对象$o$的异常程度；

        • 簇中心的点LOF接近1，但是不能认为这样的点是异常的；